

20×18位符号定点乘法器的设计及FPGA实现
模拟技术
描述
随着计算机和信息技术的快速发展,人们对器件处理速度和性能的要求越来越高,在高速数字信号处理器(DSP)、微处理器和RSIC等各类芯片中,乘法器是必不可少的算术逻辑单元,且往往处于关键延时路径中,乘法运算需要在一个时钟周期内完成,它完成一次乘法操作的周期基本上决定了微处理器的主频,因此高性能的乘法器是现代微处理器及高速数字信号处理中的重要部件。目前国内乘法器设计思想有4种,分别为:并行乘法器、移位相加乘法器、查找表乘法器、加法树乘法器。其中,并行乘法器易于实现,运算速度快,但耗用资源多,尤其是当乘法运算位数较宽时,耗用资源会很庞大;移位相加乘法器设计思路是通过逐项移位相加实现,其耗用器件少,但耗时钟,速度慢;查找表乘法器将乘积直接放在存储器中,将操作数作为地址访问存储器,得到的输出数据就是乘法结果,该方法的速度只局限于存储器的存储速度,但随乘数的位数增加,存储器的空间会急剧增加,该方法不适合位数高的乘法操作;加法树乘法器采用流水线结构,能在一个时钟完成两数相乘,但当乘数的位数增加,流水线的级数增多,导致会使用很多寄存器,增加器件的耗用,而采用Booth算法的乘法器,会在速度、器件、精度、功耗方面有很大优势。
在此介绍了20×18比特定点阵列乘法器的设计,采用基4-Booth算法,4-2压缩,基本逻辑单元为中芯国际(SMIC)公司O.18/μm工艺所提供的标准单元库,在减少乘法器器件的同时,使系统具有高速度,低功耗的特点,并且结构规则,易于FPGA的实现,同时在ASIC设计中,也是一种很好的选择。
l 乘法器结构
20×18位乘法器的逻辑设计可分为:Booth编码,部分积的产生,4-2压缩树,超前加法器,舍人溢出处理。其中。Booth算法可以减少50 %的部分乘积项,而4-2压缩树,减少求和的加数个数,它可以减少加法器个数,节省器件,与传统方法比,同时少了串行累加或Wallace树结构中的多级传递延迟,从而提高整个乘法器的速度。
4-2压缩完后最后的两个数,直接相加,其延时为一个超前进位加法器的延时,得到结果后,再根据需要数据的精度,做溢出处理及四舍五入如图1所示。
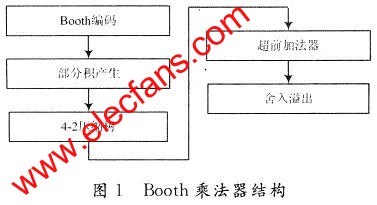
1.1 Booth编码与部分积的设计
在此采用的是基4-Booth编码方式。在补码表示的二进制数据中,扩展其最高位,并无影响。乘数A位宽为N,若N为奇数将A作符号扩展为A',使其位宽为偶数。设定:经过处理以后,乘数A'宽度为H,H为偶数且不得小于N。则乘数A'可表示为:
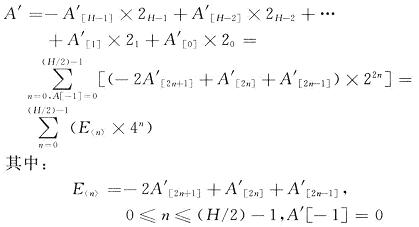
其值如表1所示:
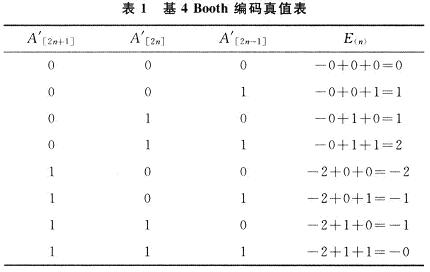
可以看到:基4布思编码一次考虑了3位:本位、相邻高位、相邻低位;处理了2位,确定运算量0,1B,2B,形成(H/2)项编码项、乘积项。对于2B的实现,只需要将B左移1位。因此,不管从那方面来说,基4算法方便又快捷。而基2算法1次只考虑2位、处理1位,形成N项编码项、乘积项,只是方便而已。SMIC提供的O.18 vm标准单元库中,布思编码逻辑表达式为:
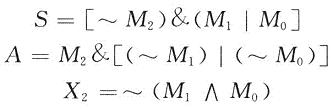
以M2指示相邻高位,以M1指示本位,以M0指示相邻低位。S为0时正,为1时负;A为0时操作数为0,为1时操作数为B;X2为O时操作数为0,为1时操作数为28。对于0,B,2B都比较好实现,2B=(B<<1);对于(-2B)实现如下:一2B=2×(-B)=[~(B<<1)]+1在硬件实现中,相邻部分积之间的权相差4,也就是部分积之间错开两位,把加1拿出来;对于所有As为1时,把所有的加1拿出来单独做部分积,这样可以省去多个加法器,节省器件。对与一个18 b的乘数,可以产生9个部分积,改进此Booth编码,再加上一个补1的数,一共产生10个加数。
1.2 4-2压缩逻辑实现
4-2压缩原理图如图2所示。它有5个输入端:A,B,C,D,ICI;三个输出端:S,CO,ICO。将5-3编码器并成1行,即为5-3计数行;若将相邻低位之ICO接入本位之ICI,则成为4-2压缩器。这样可以减少2个操作数。5-3计数器代数运算式如下:
S+CO×2+ICO×2=A+B+C+D+ICI
即:I0,I1,I2,I3,Ci,D权值为1;C,C0权值为2。
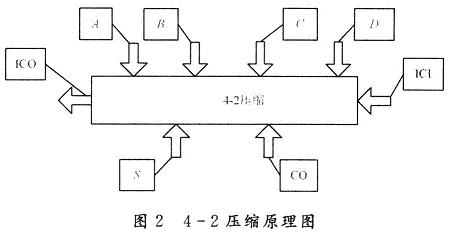
SMIC提供的0.18 vm标准单元库中,4-2压缩CMPR42的逻辑表达式为:
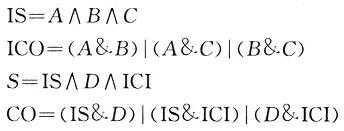
在硬件实现该模块时,因为有10个部分积,一共调用4-2压缩4次,分为3级,从顶到底为2—1—1型。4-2压缩互联如图3所示。
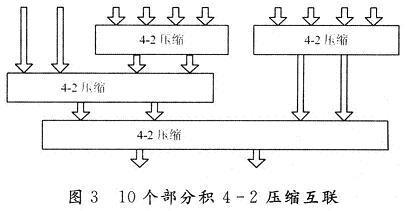
1.3 溢出处理及四舍五入
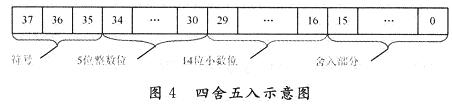
定点数相乘不会溢出,只不过结果的最终位数有所增加。20 b×18 b结果为38 b。有时38 b并不全部存储,只需其中的一些位就可以。这涉及到四舍五人。假设数A共20位,1位符号,5位整数位,14位小数位,数B共18位,1位符号位,2位整数位,15位小数位,结果格式同A。
如图4所示,因为只保留5位整数,把前3位都看成是符号位,如果不同,说明溢出;反之,没溢出。再根据前两位真正的符号判断是上溢还是下溢,若为O,则上溢,为20'h7ffff,反之,下溢,为20'h80001。在逻辑设计上用个选通可以实现,Verilog HDL代码为:assignceil=data in[37]:20'h80001:20'h7ffff;其中data in[37]为最高位。
由于Verilog HDL语言是应用最为广泛的硬件描述语言之一,可以进行各种层次的逻辑设计,也可以进行仿真验证,时序分析,并且可移植到不同产家的不同芯片中,代码可读性比较强,因此本模块设计用Ver-ilog HDL语言。
如果要舍入的数没有溢出,那么还要考虑小数部分的舍入。若舍入数为正数,舍入相邻位为1,舍入时必须进1;反之不用。若舍人数为负数,舍入相邻位为1且舍人相邻位后面还有一位为1,则舍入时需加1;反之,不加1。
2 32位浮点乘法器的实现与仿真测试
该模块仿真实现用Mentor Graphics公司的Model-Sim SE 6.0d仿真软件,图5列出本设计的:FPGA仿真结果。图5中in1是被乘数20 b。in2是乘数18 b。reset是复位清零信号,低电平有效。booth_mulTIplier_out是用Booth编码乘法器算出来的结果38 b。derect_multiplier_out是直接用乘号“×”得到的结果,也是18 b。两者结果一致。round_out是舍入后的结果,20 b。eq是测试时加的一个1 b信号,如果booth_multiplier_out和derect_multiplier_out相等为1,否则为0。
由于在测试时,将输入和输出都用寄存器锁存了一个时种clk,最后输出结果延了2个时种clk,在图5中,第一个时种clk,输入乘数和被乘数分别为126 999,68 850;输出结果为第3个时种clk的8 743 881 150。因为126 999×68 850=8 743 881 150,故结果正确。在测试时,因实际数据量比较大,in1从-219~219-1,ModelSim SE 6.0d仿真软件需要运行大概1 min,若in1从-219~219-1,in2从-217~217-1大概需要时间T=218min=4 369 h="182" day,因此在PC机上不能全测,故在写testbench时,用random函数产生随机数测试,该乘法器用ModelSim仿真软件运行12 h,eq信号始终为1,即乘法器算出的结果与直接乘的结果一致,认为该方法完全可行。
3 性能比较与创新
该模块用Synplify Pro8.1综合,用XilinxISE 7.1i实现布局布线。在Xilinx ISE中ImplementDesign下Map报告系统占用资源如表2所示。
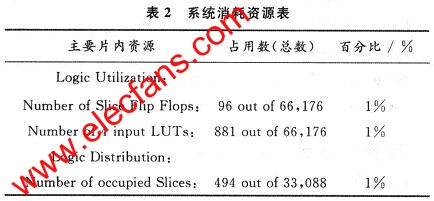
而静态时序分析报告显示速度和延时分别为62.805 MHz,15.922 ns。
该设计采用高压缩率的4—2压缩算法,压缩率为50%,而一般的3-2压缩压缩率为33%,并且采用先进的集成电路制造工艺,使用SMIC公司O.18μm的标准单元库,因此在提高了速度的同时,能减少器件,该乘法器能在1个时钟内完成,不像采用流水线结构,虽然可以提高速度到105.38 MHz,但需3个时钟,需要大量锁存器,从而在增加器件的同时增加功耗,而且完成一次乘法运算时间要24.30 ns。因国内集成电路制造起步晚,目前中国80%的集成电路设计公司还在采用0.35/μm及以下工艺,国内同类乘法器,采用上华0.5 μm的标准单元库,完成1次乘法运算时间接近30 ns,逻辑单元是1 914个。但该设计完成1次乘法运算时间仅15.922 ns,器件只有494个Slices,性能明显提高。
4 结 语
给出了20×18位符号定点乘法器的设计,整个设计采用了Verilog HDL语言进行结构描述,采用的器件是xc2vp70-6ff1517。该设计采用基4 Booth编码,4-2压缩,以及采用SMIC0.18μm标准单元库,使得该乘法器面积降低的同时,延时也得到了减小,做到芯片性能和设计复杂度之间的良好折中,该设计应用于中国地面数字电视广播(DTMB)ASIC中3 780点FFT单元的20×18位符号定点乘法器,在60 MHz时工作良好,达到了预定的性能要求,具有一定的实用价值。
-
fpga中定点乘法器设计(中文)2012-08-12 0
-
分享--fpga中定点乘法器设计(中文)2012-08-24 0
-
FPGA乘法器设计2018-02-25 0
-
怎么设计基于FPGA的WALLACETREE乘法器?2019-09-03 0
-
硬件乘法器是怎么实现的?2023-09-22 0
-
Altera FPGA内置的乘法器为何是18位的?2023-10-18 0
-
一种用于SOC中快速乘法器的设计2009-09-21 826
-
1/4平方乘法器2010-05-18 1815
-
变跨导乘法器2010-05-18 1114
-
基于IP核的乘法器设计2011-05-20 837
-
基于FPGA的WALLACE TREE乘法器设计2011-11-17 4972
-
定点乘法器设计(中文)2012-01-17 660
-
华清远见FPGA代码-FPGA片上硬件乘法器的使用2016-10-27 539
-
使用verilogHDL实现乘法器2018-12-19 10517
-
FPGA中乘法器的原理分析2020-09-27 9033
全部0条评论

快来发表一下你的评论吧 !

