如何用matlab实现针对四面体单元划分的三维结构进行有限元编程

导读：自9月以来，我的《教你Matlab有限元编程对悬臂梁进行受力分析》原创文章发布以来，我的精品课《Matlab有限元编程从入门到精通10讲》受到了越来越多的工程师朋友的关注，已超过50多人已经订阅学习，欢迎大家加入订阅用户交流群一起讨论Matlab有限元编程那些事（哈哈哈，为大家答疑和分享资料）。

今天，我接着分享Matlab有限元编程专业技能。之前的课程我们学习了一维梁单元，二维平面单元，三维板壳单元的matlab有限元编程，本次案例主要讲解如何用matlab实现针对四面体单元划分的三维结构进行有限元编程，具体案例是一个悬臂梁受集中荷载的问题。图1为本案例Matlab编程计算得到的结果。主要内容涉及四面体单元的有限元基本理论的推导，主要是单元刚度矩阵的推导，此外还包括等参单元和Hammer数值积分以及三维问题的后处理计算。

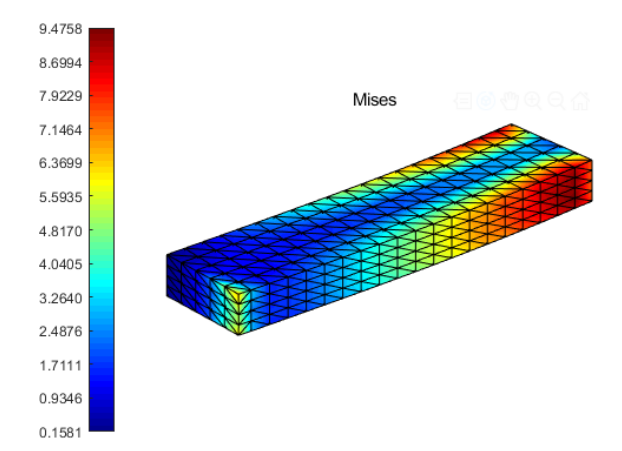
图1 悬臂梁受集中荷载的应力云图

一个完整的有限元程序基本组成部分包括前处理模块、分析主程序模块和后处理模块。在前处理模块中，实现节点坐标输入、单元节点编号、网络划分以及边界条件输入等工作；在分析主程序模块中，求解整体刚度方程；在后处理模块中，实现结果显示、数据输出等工作。

对应的有限元法的基本步骤：

（1）几何域离散，获得标准化的单元； （2）通过能量原理（虚功原理或最小势能原理，获得单元刚度方程； （3）单元的集成（装配）； （4）处理位移边界条件； （5）计算位移场；

（6）计算单元的其他物理量（应力应变）。

这几步中，最核心的内容是单元研究，具体包括：

（1）节点描述（不同坐标系节点坐标的变化）； （2）场描述（位移场，应变场，应力场，形函数）；

（3）单元刚度方程（基于能量原理推导）。

需要说明的是后文的四面体单元有限元方程的推导过程是基于等参单元的基本理论从局部坐标（自然坐标、体积坐标）出发来推导四面体单元的刚度矩阵，因为这样做比较规范自然，推导过程也适用于其他类型单元。但是因为四面体单元相对简单也可以直接从直角坐标（全局坐标）进行推导，具体推导过程可参考清华大学曾攀老师的课程，直接从直角坐标（全局坐标）进行推导的过程省去了等参单元雅各比矩阵呀等坐标系映射的各种概念，理解起来相对容易。

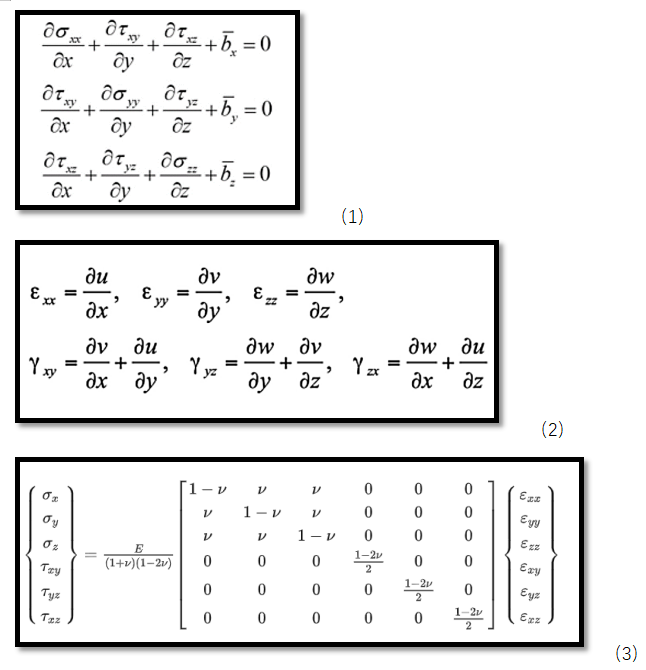
公式（1）-（3）为弹性力学中三维空间弹性问题的完整描述，分别是空间问题的平衡方程、几何方程、物理方程，这是我们推导有限元方程的基础。这些公式会在后面的有限元方程推导过程中用到。

四面体单元的坐标描述涉及了等参单元的概念，在有限元方法中，若要离散边界为曲线或曲面的求解域，需要建立将形状规则的单元变换为边界为曲线或曲面的单元的方法，在有限元法中对应此问题所采用的变换方法是等参变换，即单元几何形状的变换和单元内场函数采用相同数目的节点及相同的插值函数进行变换。四面体单元的参数坐标就是体积坐标，体积坐标的定义如图2所示。

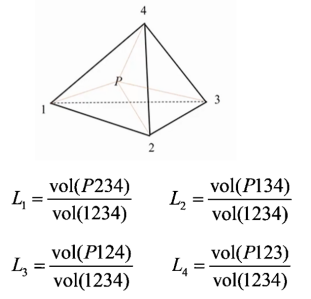
图2 四面体单元体积坐标的定义

参数坐标系下的形函数等于对应的体积坐标，四个节点对应四个形函数，如下式，

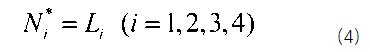
这样就实现了自然坐标系和物理坐标系下的坐标映射，如下式，

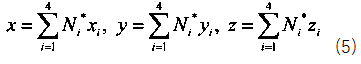
同样形函数也可以用于物理场的插值，公式（6）是位移场的插值表达式。

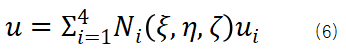
有了位移场插值的表达式就可以通过公式（2）-（3）的几何方程和物理方程推导应变场和应力场的有限元表达式，但是公式（2）的几何方程中存在对于xy也就是物理坐标系下的偏导数，代入公式（6）后也就是形函数对物理坐标的偏导数，因为我们的形函数是在自然坐标系下定义的，是关于ξ, η, ζ的函数，想要知道他对x，y的偏导，这里利用了链式求导法则，即可建立如下式（7）所示的形函数对自然坐标的物理坐标偏导数的映射关系。中间的这个矩阵就叫Jacob矩阵。

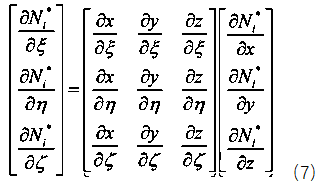
如何求Jacob矩阵呢？将公式（5）代入公式（7）可以得到如下式（8）所示的自然坐标偏导矩阵乘以一个坐标矩阵，

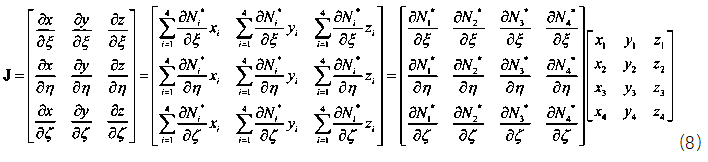
得到jacob矩阵后求逆，再乘以自然坐标偏导矩阵就可以得到形函数对物理坐标的导数。如下式（9），

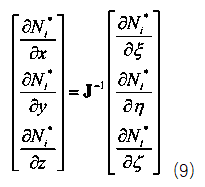
上述形函数对物理坐标的导数的求解过程对应的matlab代码如下：

 

function [NDxyz,JacobiDET] = ShapeFunction(ElementNodeCoordinate)
%计算形函数及形函数对局部坐标ksi eta zeta的导数
NDL = [-1 1 0 0;-1 0 1 0;-1 0 0 1];%3*4  [N1Dksi N2Dksi N3Dksi N4Dksi;N1Deta N2Deta N3Deta N4Deta……]
Jacobi = NDL*ElementNodeCoordinate;%计算雅可比矩阵3*4 4*3
JacobiDET = det(Jacobi);%计算雅可比行列式3*3 [DxDksi DyDksi DzDksi;DxDeta……
JacobiINV=inv(Jacobi);%对雅可比行列式求逆3*3
NDxyz=JacobiINV*NDL;%利用雅可比行列式的逆计算形函数对结构坐标的导数[DN1Dx DN2Dx DN3Dx;DN1Dy DN2Dy DN3Dy;……]
end

这样求出形函数对物理坐标的导数后就可以代入公式（2）几何方程求出应变场矩阵B，经过能量原理的推导可以得到单元刚度矩阵的表达式，注意刚度矩阵的表达式是一个积分的运算，由于被积函数较为复杂，如果代数积分进行计算要消耗大量的计算资源，因此有限元理论中引入数值积分，即我们熟悉的高斯积分和hammer积分，对于直角坐标系我们采用高斯积分，对于面积或者体积坐标系我们采用hammer数值积分，具体这两类积分的原理大家可以参考相关数值积分教材即可，这里我们只利用hammer数值积分的结论。四面体单元具体的数值积分公式如下：

 

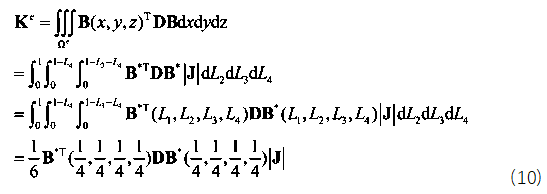
其中，对应的B矩阵如下式所示：
 

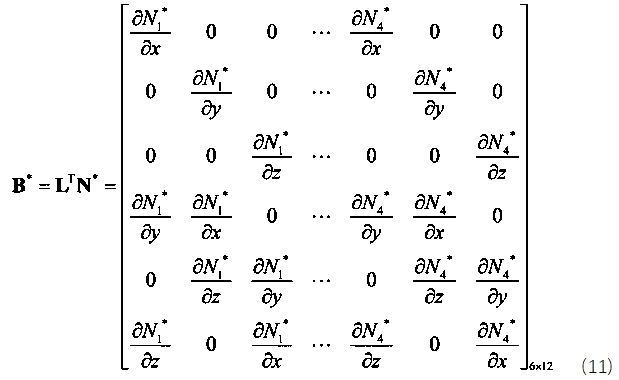
单元刚度矩阵确定好之后，将其按照自由度索引组装到全局刚度矩阵中，组装的核心思想就是确定好每个单元中的每个节点中的每个自由度在整体刚度矩阵中的位置即可。

整体刚度矩阵确定之后，就是荷载向量p的定义，这个很简单，只要依次确定每个节点每个自由度的外力荷载即可。

刚度矩阵和荷载向量确定后接下来就是边界条件的施加，大家最熟悉的可能就是直接划行划列的方法，这个方法的弊端在于划去自由度为零的行列之后，整体单元刚度矩阵的编号以及自由度编号都会改变，对于大规模计算非常不方便，影响计算效率。为了解决这个问题出现了乘大数法和置一法，置一法只能解决零边界问题，乘大数法可以解决零边界和非零边界，应用非常广泛。边界条件的施加这里我们采用乘大数法。针对边界条件采用乘大数法施加边界的方式为：在自由度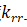上乘以一个很大的数a，然后在相应的外力向量对应的自由度上乘以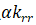，具体如下式（22）所示

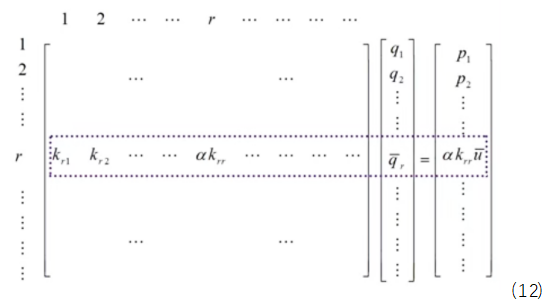
为了验证乘大数法的可靠性，将对应行列写成代数表达式的形式，如下式所示

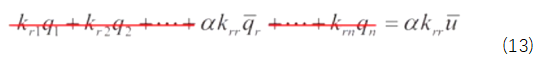
考虑到远大于，所以公式（13）可以写成， 

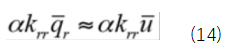
即可得到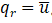。可见乘大数法与实际边界条件是等价的。

施加了边界条件的刚度矩阵K与荷载矩阵p之后，可直接利用matlab中的高斯消去法 计算符“”，完成位移的求解，即u=Kp。

求出节点位移之后通常我们做受力分析时还会需要知道应力应变的分布情况，具体通过下述公式求解：

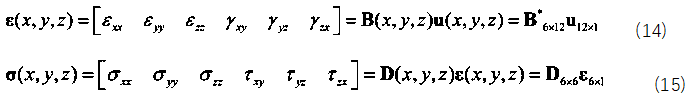
对应的提取应力和应变的后处理代码如下：

 

% 计算形函数导数
    [NDxyz, ~] = ShapeFunction(ElementNodeCoordinate);%[DN1Dx DN2Dx DN3Dx;DN1Dy DN2Dy DN3Dy;……]
    ElementNodeDisplacement=U(ElementNodeDOF);%12*1 节点位移列阵
    ElementNodeDisplacement=reshape(ElementNodeDisplacement,Dof,4);%3*4
    % 计算单元应变 Strain3_3 3*3的应变矩阵
    Strain3_3=ElementNodeDisplacement*NDxyz';%高斯积分点处应变 3*4  4*3
    %把单元应变矩阵改写成6*1
    Strain=[Strain3_3(1,1) Strain3_3(2,2) Strain3_3(3,3) ...
    Strain3_3(1,2)+Strain3_3(2,1)....
    Strain3_3(2,3)+Strain3_3(3,2) Strain3_3(1,3)+Strain3_3(3,1)]';
Stress(1:6,1) = D*Strain;%高斯积分点处应变

利用绘图命令Patch我们可以得到如图1所示的应力云图。另外计算得到的变形和位移云图如图3-4所示。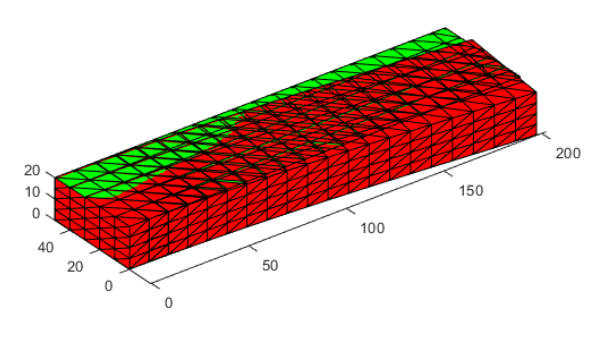



图3 变形前后的网格对比

 

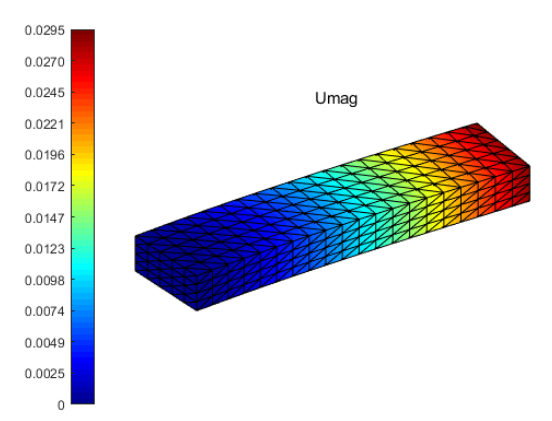
图4 位移云图

审核编辑：刘清