

MEMS惯性传感器之卡尔曼滤波
电子说
描述
01 说在前面的话
关于卡尔曼这部分内容,一直思考怎么用通俗易懂的方式来按照自己的理解梳理。但是无奈,总是绕不开用数学的方法表达那 5 个关键的公式。不论是在B站,还是各个博客都用很多的讲解。直到理解了严恭敏老师在讲卡尔曼滤波时的一个温度估算举例,才斗胆引用下面文章,来填写卡尔曼滤波这个坑。
一个简单的应用是估计物体的位置和速度。简要描述如下:假设我们可以获取一个物体的包含噪声的一系列位置观测数据,我们可以获得此物体的精确速度和位置连续更新信息。例如,对于雷达来说,我们关心的是跟踪目标,而目标的位置、速度、加速度的观测值是时刻含有误差的,卡尔曼滤波器利用目标的动态信息,去掉噪声影响,获取目标此刻好的位置估计(即滤波过程),将来的位置估计(即预测过程),也可以是过去位置估计的(即插值或平滑过程)。
02应用举例
假设我们要研究的对象是一个房间的温度。根据你的经验判断,这个房间的温度是恒定的,也就是下一分钟的温度等于现在这一分钟的温度(假设我们用一分钟来做时间单位)。 假设你对你的经验不是绝对相信,可能会有上下偏差几度。我们把这些偏差看成是高斯白噪声(White Gaussian Noise,理想情况下我们以高斯噪声来进行假设估计),也就是这些偏差跟前后时间是没有关系的而且符合高斯分布(Gaussian Distribution)。 另外,我们在房间里放一个温度计,但是这个温度计也不准确的,观测值会比实际值偏差。我们也把这些偏差看成是高斯白噪声。好了,现在对于某一分钟我们有两个有关于该房间的温度值:你根据经验的预测值(系统的预测值)和温度计的值(观测值)。下面我们要用这两个值结合它们各自的噪声来估算出房间的实际温度值。 假如我们要估算k时刻的实际温度值。首先你要根据k−1时刻的温度值,来预测k时刻的温度。因为你相信温度是恒定的,所以你会得到k时刻的温度预测值是跟k−1时刻一样的,假设是23度,同时该值的高斯噪声的偏差是5度(5是这样得到的:如果k−1时刻估算出的最优温度值的偏差是3,你对自己预测的不确定度是4度,它们平方相加再开方就是5)。 然后,你从温度计那里得到了k时刻的温度值,假设是25度,同时该值的偏差是4度。由于我们用于估算k时刻的实际温度有两个温度值,分别是23度和25度。究竟实际温度是多少呢?相信自己还是相信温度计呢?究竟相信谁多一点,我们可以用它们的协方差(covariance)来判断。因为 Kg^2=5^2/(5^2+4^2),所以Kg=0.78,我们可以估算出k时刻的实际温度值是:23+0.78∗(25−23)=24.56度。
可以看出,因为温度计的协方差比较小(比较相信温度计),所以估算出的最优温度值偏向温度计的值。现在我们已经得到k时刻的最优温度值了,下一步就是要进入k+1时刻,进行新的最优估算。在进入k+1时刻之前,我们还要算出k时刻那个最优值(24.56 度)的偏差。算法如下:

这里的5就是上面的k时刻你预测的那个23度温度值的偏差,得出的2.35就是进入k+1时刻以后k时刻估算出的最优温度值的偏差(对应于上面的3)。就是这样,卡尔曼滤波器就不断的把协方差递归,从而估算出最优的温度值。它运行的很快,而且它只保留了上一时刻的协方差。上面的Kg,就是卡尔曼增益(Kalman Gain),可以随不同的时刻而改变自己的值。
03卡尔曼滤波器算法
卡尔曼滤波基于时域描述的线性动态系统,它的模型是马尔科夫链(Markov Chain),而马尔科夫链建立在一个被高斯噪声干扰的线性算子之上。 系统的状态可以用一个元素为实数的向量表示。随着离散时间的增加,这个线性算子就会作用到当前状态之上,产生一个新的状态,并且会带入一定的噪声,同时一些已知的控制信息也会加入。同时,另外一个受噪声干扰的线性算子将产生这些隐含状态的可见输出。卡尔曼滤波器可以被看作为类隐马尔科夫模型,它们的显著不同点在于:
隐状态变量的取值空间是一个连续的空间,而不是离散的状态空间;
另外,隐马尔科夫模型可以描述下一个状态的一个任意分布,这也与应用于卡尔曼滤波器中的高斯噪声模型相反。
先看一下动态系统的基本模型。
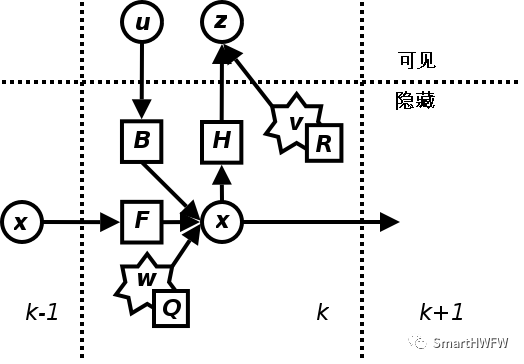
首先,我们先要引入一个离散控制过程的系统。该系统的过程模型可用一个线性随机微分方程(Linear Stochastic Difference Equation)来描述:

再加上系统观测模型:
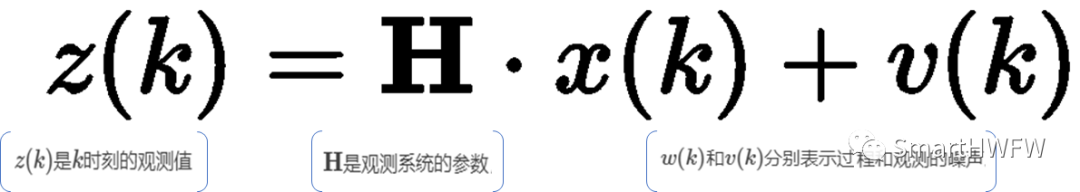
卡尔曼滤波是一种递归的估计,即只要获知上一时刻状态的估计值以及当前状态的观测值就可以计算出当前状态的估计值,因此不需要记录观测或者估计的历史信息。卡尔曼滤波器与大多数滤波器不同之处在于:它是一种纯粹的时域滤波器,它不需要像低通滤波器等频域滤波器那样,需要在频域设计再转换到时域实现。卡尔曼滤波器的操作包括两个阶段:预测与更新:
在预测阶段,滤波器使用上一状态的估计,做出对当前状态的估计。
在更新阶段,滤波器利用对当前状态的观测值优化在预测阶段获得的预测值,以获得一个更精确的新估计值。
03.1 预测阶段
对于满足上面的条件(线性随机微分系统,过程和观测都是高斯白噪声),卡尔曼滤波器是最优的信息处理器。
下面我们来用它们结合它们的协方差来估算系统的最优化输出(类似上一节那个温度的例子)。首先,我们要利用系统的过程模型,来预测下一状态的系统。假设现在的系统状态是k,根据系统的模型,可以基于系统的上一状态而预测出现在状态(称为预测的状态估计方程):
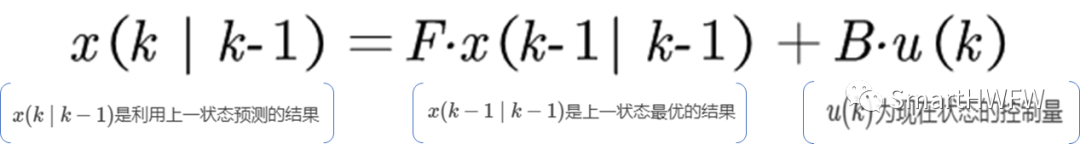
到现在为止,我们的系统结果已经更新了,可是,对应于x(k∣k−1)的协方差(covariance)还没更新。我们用P表示协方差,它实际上描述了预测值的准确程度(称为预测的协方差矩阵估计方程):
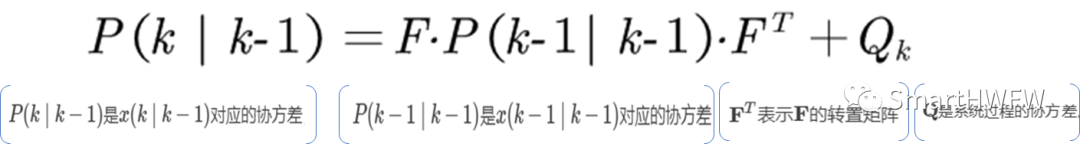
03.2 更新阶段
在进行更新之前,我们先计算三个值: 首先是观测余量(measurement residual):
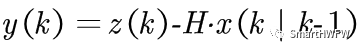
因为观测过程中存在一个观测误差的协方差矩阵,我们可以给出一个观测余量的协方差:
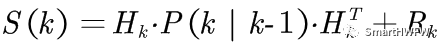
接下来给出一个卡尔曼增益(Kalman Gain):
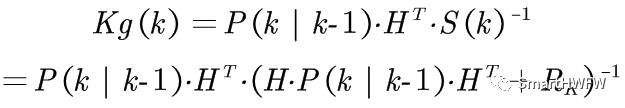
现在我们有了现在状态的预测结果,然后我们再收集现在状态的观测值。结合预测值和观测值,我们可以得到现在状态k的最优化估算值x(k|k)(称为更新的状态估计方程):

到现在为止,我们已经得到了k状态下最优的估算值x(k∣k)。但是为了要使得卡尔曼滤波器不断的运行下去直到系统过程结束,我们还要更新k状态下x(k∣k)的协方差(称为更新的协方差矩阵估计方程):
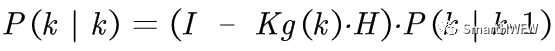
其中 I 为单位矩阵,对于单模型单观测,I=1。当系统进入k+1状态时,P(k∣k)就是预测方程中的P(k−1∣k−1)。这样,算法就可以自回归的运算下去。
03.3 算法流程抽象
1)先决定当前系统的初始状态,并根据预测方程(过程模型)得到一个下一个时刻预测的状态;
2)根据预测方程中过程的误差,得到当前预测的协方差估计;
3)进入更新阶段,我们根据目前系统的观测值和上一个时刻预测的状态,从转换方程(观测模型)入手,得到一个测量余量;
4)根据转换方程和上个时刻预测的协方差估计,也可以得到一个测量余量的协方差估计;
5)根据 a)测量余量的协方差Sk∣k; b)转换方程H和 c)上个时刻的预测协方差估计Pk∣k−1,我们得到卡尔曼增益Kk∣k;
6)根据卡尔曼增益和测量余量,我们从预测的状态中更新优化当前的状态的值,而这个值可以用来预测下一个时刻的状态;
7)同样,我们根据 a)卡尔曼增益Kk∣k 和 b)上个时刻的预测协方差估计Pk∣k−1,我们把当前更新阶段的协方差Pk∣k估计也得到,帮助下一时刻的卡尔曼增益计算。
审核编辑:汤梓红
-
3种算法测试,告诉你为什么四轴飞行器上使用卡尔曼滤波最好?2015-06-11 0
-
【心得】分享我对于卡尔曼滤波用于传感器融合的见解2015-06-12 0
-
ADIS16480 具有动态方位输出的10自由度MEMS惯性传感器2015-12-24 0
-
10自由度MEMS惯性传感器ADIS164802018-10-15 0
-
装配MEMS惯性传感器的实用方法2018-11-12 0
-
精密MEMS惯性传感器ADIS16334和ADIS16375的特点与功能框图2018-12-04 0
-
项目应用中的卡尔曼滤波2019-05-22 0
-
MEMS惯性传感器与工业环境2019-09-03 0
-
MEMS惯性传感器的优势是什么?2019-11-05 0
-
MEMS惯性传感器的测试及应用领域2020-05-18 0
-
惯性测量单元3DM-GX5-15 传感器2020-12-07 0
-
卡尔曼滤波有哪些应用2021-07-12 0
-
卡尔曼滤波器的使用原理2021-08-17 0
-
卡尔曼滤波器是什么2021-11-16 0
-
有没有基于9轴传感器的三阶卡尔曼滤波器算法?2023-11-06 0
全部0条评论

快来发表一下你的评论吧 !

