触摸屏系统中校准的简单易懂的说明

机械未对准和比例因子导致来自触摸屏面板（由触摸屏控制器转换）的值与安装触摸屏面板的显示器（通常为 LCD）之间的不匹配。本教程讨论如何校准触摸屏面板以匹配显示器。

介绍

机械未对准和比例因子可能导致触摸屏系统（在本教程中，触摸屏系统意味着由触摸屏和触摸屏控制器组成的设置）与安装触摸屏的显示器（通常为 LCD）的值不匹配。本文讨论了校准触摸屏系统的数学技术，以便将显示上的图形与触摸屏控制器的输出相匹配。

了解图像转换：平移、旋转和缩放

图1是LCD触摸屏显示器上显示的圆圈可能发生的失真的夸大视图。当手指绕着圆圈（红线）描摹时，触摸屏系统可能会给出椭圆（蓝线）而不是圆的坐标，如图1所示。形状从圆形到椭圆的这种变化可以通过以下图形转换来解释：平移、旋转和缩放。

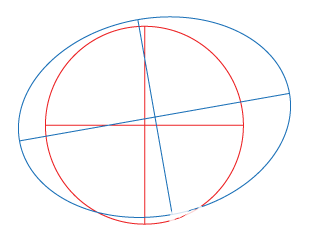
图1.由于显示器和触摸屏系统不匹配，圆圈在触摸屏上会改变形状。

直觉表明，x-y 平面中任何经过变换的坐标点 x， y 都应该如下所示：

 

xNEW = f1(xOLD, yOLD) + constant1	(Eq. 1a)
yNEW = f2(xOLD, yOLD) + constant2	(Eq. 1b)

 

其中 x新增功能和 y新增功能是转换后的坐标;x老和 y老是旧坐标;f1（） 和 f2（） 是转换旧坐标的函数;常量 1 和 2 就是常量。

如果变换是线性的，则函数 f1（） 和 f2（） 可以用以下等式替换：

 

xNEW = A xOLD + B yOLD + C	(Eq. 2a)
yNEW = D xOLD + E yOLD + F	(Eq. 2b)

 

其中 A、B、C、D、E 和 F 是常数系数。

请注意，f1() = A xOLD +B yOLD and f2() = D xOLD + E yOLD, 其中常量 1 和常量 2 分别是 C 和 F。

平移、旋转和缩放背后的数学原理

一个显示图形变换的示例将证明本练习的最终变换方程将导致上述方程 2a 和 2b，因此，我们的直觉成立。（用户可以绕过此示例，直接跳转到下面的三点校准和 N 点校准讨论。

下图（图 2）显示了一个经过平移、旋转和缩放的正方形（形状 A）（形状 B）。在此过程中，它被转换为矩形。

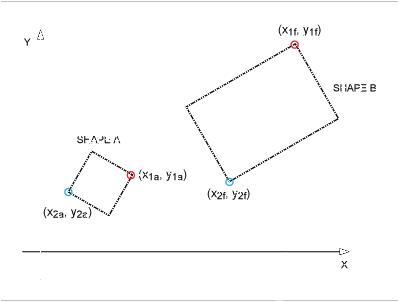
图2.平移、旋转和缩放将正方形转换为矩形。

要旋转和缩放正方形（形状 A），重要的是首先将其中心移动到原点（图 3），以确保旋转和缩放均匀发生。

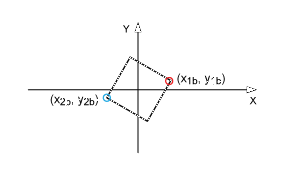
图3.移动图 2（形状 A）的正方形，使其中心位于 x-y 轴的原点上。

向中心移动或向中心平移将更改正方形所有坐标的值。为简单起见，这里只有 x 的变换1， y1在图 2 中将进行探讨。因此，x1一， y1一转换为 x1b， y1b代表这个新数字的新方程是：

 

x1b= x1一+ Tx0	（公式3a）
y1b= y1一+ TY0	（公式3b）

 

旋转上图，以便在 x 和 y 方向上进行适当的缩放。图4显示该图已逆时针旋转角度θ。

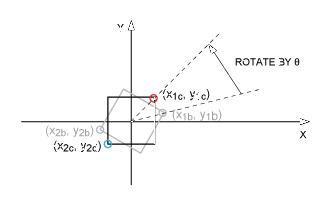
图4.按照等式3，正方形逆时针旋转。

新坐标 （x1c， y1c） 旋转后如下所示。（请参阅附录，了解此旋转方程的推导。

 

x1c = x1b Cosθ - y1b Sinθ	(Eq. 4a)
y1c = x1b Sinθ + y1b Cosθ	(Eq. 4b)

 

将等式3a和3b代入等式4a和4b，并简化：

 

x1c = x1a Cosθ - y1a Sinθ + Kx	(Eq. 5a)
y1c = x1a Sinθ + y1a Cosθ + Ky	(Eq. 5b)

 

其中Kx = Tx0 Cosθ - Ty0 Sinθ and Ky = Tx0 Sinθ + Ty0 Cosθ.

现在，在 x 和 y 方向上缩放正方形，使其与图 2（形状 B）中的矩形大小相同。如果我们说Gx是 x 方向和 G 方向上的比例因子y是 y 方向上的比例因子，则正方形将转换为矩形（图 5）。

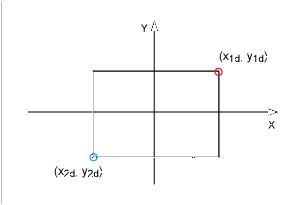
图5.使用比例因子 G 将正方形转换为矩形x对于 x 方向，和 Gy对于 Y 方向。

将公式 5a 和 5b 乘以比例因子 Gx和 Gy公式6a和6b是图5所示矩形的坐标。

 

x1d = x1a Gx Cosθ - y1a Gx Sinθ + Kx Gx	(Eq. 6a)
y1d = x1a Gy Sinθ + y1a Gy Cosθ + Ky Gy	(Eq. 6b)

 

将矩形旋转 a，使其与图 2 中形状 B 的旋转方向匹配。这导致 （x1d， y1d） 到 （x1e， y1e），如图 6 所示。

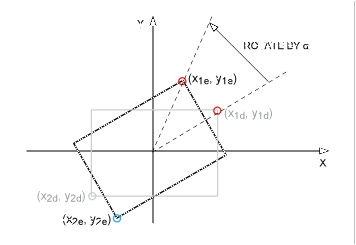
图6.旋转图 5 的矩形，使其与图 2 中形状 B 的方向相匹配。

再次逆时针旋转。（x1e， y1e） 在 （x1d， y1d） 是：

 

x1e = x1d Cosα - y1d Sinα + Kx	(Eq. 7a)
y1e = x1d Sinα + y1d Cosα + Ky	(Eq. 7b)

 

将等式6a和6b代入等式7a和7b，并简化：

 

x1e = x1a A + y1a B + P	(Eq. 8a)
y1e = x1a D + y1a E + Q	(Eq. 8b)

 

其中：
A = Gx Cosθ Cosα - Gy Sinθ Cosα
B = - Gx Sinθ Cosα - Gy Cosθ Cosα
P = Kx Gx Cosα - Ky Gy Sinα
D = Gx Cosθ Sinα + Gy Sinθ Cosα
E = -Gx Sinθ Sinα + Gy Cosθ Cosα
Q = Kx Gx Sinα + Ky Gy Cosα

现在需要完成平移（图 7），将旋转的矩形移动到图 2 中形状 B 出现的位置。

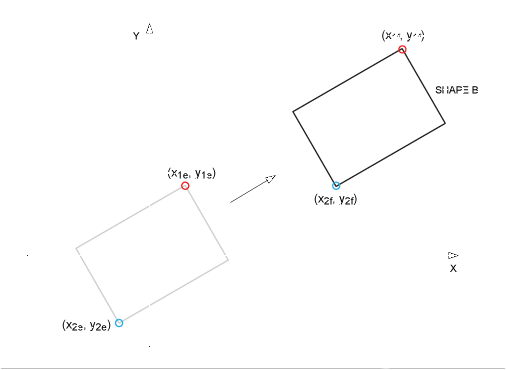
图7.矩形从原点到图 2 中形状 B 出现的位置的平移。

假设 x 和 y 方向的平移为 Tx和 Ty分别。因此，等式8a和8b将变为：

 

x1f = x1a A + y1a B + C	(Eq. 9a)
y1f = x1a D + y1a E + F	(Eq. 9b)

 

其中 C = P + Tx和 F = Q + Ty.

等式 9a 和 9b 就是我们想要的——它们与等式 1a 和 1b 相匹配。请注意，坐标 （x1楼， y1楼） 是 （x1一， y1一).在安装在显示器上的触摸面板中，用户必须在校准期间确定 A、B、C、D、E 和 F。

请注意，本练习的目的是让用户了解变换方程的一般形式，如公式 9a 和 9b 所示。本文表明，无论旋转、平移和缩放的方向和大小如何，我们都将达到这种一般形式。

三点校准

我们从一对方程开始，这是我们上面数学练习中的最后一对。

 

x1f = x1a A + y1a B + C	(Eq. 9a)
y1f = x1a D + y1a E + F	(Eq. 9b)

 

触摸屏系统校准的目标是求解公式2a和2b（或类似的公式9a和9b），以推导出A、B、C、D、E和F的值。

看看这些方程，我们知道有六个未知数。因此，我们需要六个方程来求解这些未知数，这可以通过对触摸屏系统进行三点校准来实现。用户将通过触摸面板上的三对显示坐标来生成三对 （x， y） 坐标：（x1d， y1d）， （x2d， y2d） 和 （x3d， y3d).如果它们对应的触摸屏值（由触摸屏控制器显示）为 （x1， y1）， （x2， y2） 和 （x3， y3），那么六个未知数可以通过下面显示的方程求解。这些点必须彼此独立，如图 8 所示。

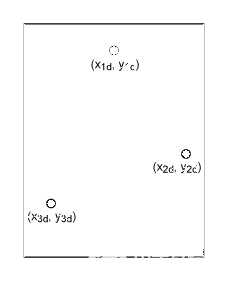
图8.LCD面板显示三个显示坐标供用户触摸。

x1d= x1A + y1B + C
x2d= x2A + y2B + C
x3d= x3A + y3B + C

y1d= x1D + y1E + F
y2d= x2D + y2E + F
y3d= x3D + y3E + F

现在有了六个未知数的六个方程，以上可以用矩阵形式写成：

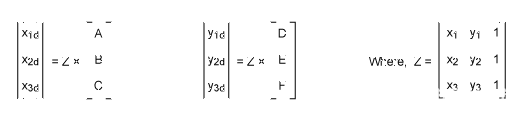
因此，稍微进行一些矩阵操作将产生 A、B、C、D、E 和 F，如下所示：

哪里Z-1是 Z 的逆矩阵。

三点校准示例

本例将使用MAX11800触摸屏控制器。假设 LCD 面板显示器的分辨率为 256 x 768，并且选择的三个校准点是 （65， 350）、（200， 195） 和 （195， 550）。这些是我们希望触摸面板在触摸时显示的确切点。但是，由于MAX11800的分辨率为4096 x 4096 （12位），并且由于机械未对准，坐标会有所不同。在本练习中，我们假设这些值分别为：（650， 2000）、（2800， 1350） 和 （2640， 3500）。请注意：这些值仅供参考。

使用公式 10a 和 10b 求解 A、B、C、D、E 和 F，我们得到以下结果：

A = 0.0635
B = 0.0024
C = 18.9116
D = -0.0227
E = 0.1634
F = 37.8887

因此，将为此特定示例生成 x 和 y 坐标的方程为：

xd= 0.0635 x + 0.0024 y + 18.9116
yd= -0.0227 x + 0.1634 y + 37.8887

其中 （x， y） 是来自触摸屏系统的坐标，（xd， yd） 是调整后的值。

N 点校准

用户可以选择使用更多点进行校准。方程组的广义形式如下所示：

 

x1d = x1 A + y1 B + C x2d = x2 A + y2 B + C x3d = x3 A + y3 B + C ... xnd = xn A + yn B + C

(Eq. set 11a)

y1d = x1 D + y1 E + F y2d = x2 D + y2 E + F y3d = x3 D + y3 E + F ... ynd = yn D + y3 E + F

 

其中，（x1d， y1d)...（x德·， y德·） 是显示生成的坐标;（x1， y1)...（xn， yn）是MAX11800从触摸屏面板确定的相应值（n个点）。目标是使用这些值确定系数。

在方程集 11a 中，有三个未知数，A、B 和 C，但坐标集大于三个。这意味着方程多于未知数。因此，在这种情况下，使用最小二乘拟合来利用所有点并推导出系数的平均值是有意义的。这也意味着更多的校准点将有助于降低误差。最小二乘拟合如图 9 所示。相同的技术将应用于确定 y 值的未知数 D、E 和 F。

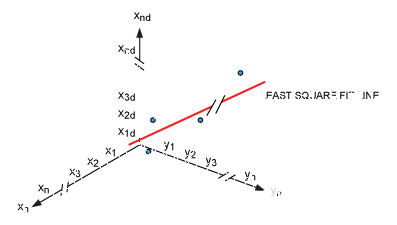
图9.系数 A、B 和 C 的平均值是通过对点应用最小二乘拟合来找到的。

方程集 11a 和 11b 可以写成矩阵形式，如下所示：

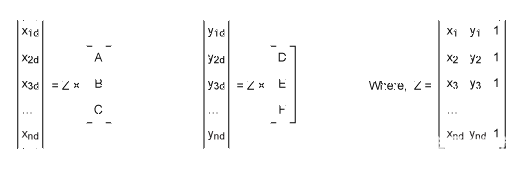
通过在此矩阵形式中使用最小二乘拟合，系数由以下方程给出。（请参阅一本关于回归分析的书，了解最小二乘拟合形式的矩阵形式的推导。

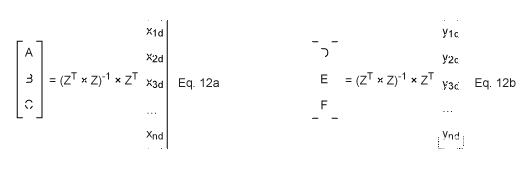
N 点校准示例

再次假设 LCD 面板显示器的分辨率为 256 x 768，五个校准点分别为 （100， 350）、（50， 200）、（200， 200）、（210， 600） 和 （65， 600）。这些是我们希望触摸面板在触摸时显示的确切点。但是，由于MAX11800的分辨率为4096 x 4096 （12位），并且由于机械未对准，因此这些点可能会有所不同。再次假设它们分别是 （1700， 2250）、（750， 1200）、（3000， 1500）、（2500， 3400） 和 （600， 3000）。请注意：这些值是虚构的，仅供参考。

使用等式 12a 和 12b 求解 A、B、C、D、E 和 F，我们得到：

A = 0.0677
B = 0.0190
C = -33.7973
D = -0.0347
E = 0.2100
F = -27.4030

因此，为此特定示例生成 x 和 y 坐标的公式为：

xd= 0.0677 x + 0.0190 y - 33.7973
yd= -0.0347 x + 0.2100 y - 27.4030

其中 （x， y） 是来自触摸屏控制器的坐标，以及 （xd， yd） 是调整后的坐标值，以匹配显示屏上显示的内容。

示例摘要

如果在三个点上使用最小二乘技术，它将产生与三点校准相同的系数。因此，在数学上，将三点校准处理为具有三个未知数的三个联立线性方程组比使用最小二乘技术进行较长的计算更容易。

审核编辑：郭婷