

看完学会速傅立叶变换FFT
电子说
描述
FFT 即快速傅立叶变换。在很多计算机领域都用用处,例如数字图像处理、计算机网络。但他在算法竞赛中主要是用于多项式和生成函数相关的题目。
多项式
表达方式
简介
- 系数表达式,即。
- 坐标形式。每一个坐标用表示。显然,为了能够表示一个确定的多项式,需要个不同的坐标来表示。
比较
- 对于系数表示,多项式加法的时间复杂度是,多项式乘法的时间复杂度是。
- 对于点值表示,多项式加法的时间复杂度同样是,但是乘法的时间复杂度就是(因为多项式乘法以后最高项次数为,我们只需要个坐标表示)。
思考
这样一来,我们就有一个想法,多项式乘法,是不是可以利用坐标表示做多项式乘法特别快这点来优化算法。
于是需要解决的最大的问题就是,多项式两种表示方法之间的互相转换。
求值朴素做法的时间复杂度是,即随便选取一个值带入,暴力计算。
差值朴素的做法时间复杂度是,即根据坐标进行高斯消元。
在介绍 FFT 之前,得先学习 DFT (离散傅里叶变换)算法。
DFT
由于对一个多项式的点值表达式的取是任意的,所以好的取法可能会使一个算法产生本质性的蜕变。
我们选取次单位复根作为来取值。
单位复根
,这个方程的复数根为次单位根。
单位的个单位根分别为。
个单位根在复平面的坐标表示为,我们将这个记为。在复平面上形象的表示的话,就是下图:
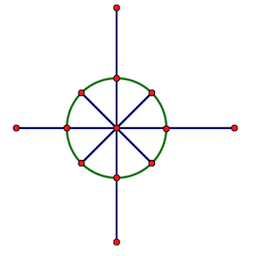
单位根在多项式的应用
我们将个单位根带入多项式可以得到个因变量结果,记为。
我们将个单位根的倒数作为自变量带入由作为系数的多项式,可以得到。
而当的时候,它为,其余时候,它为(通过等比数列求和)。于是有。
于是可以发现,将个单位根的倒数带入变换后的多项式,可以得到原来的多项式。
这样一来,我们利用个单位根的性质,完成了多项式两种表示方式之间的转换。
DFT算法
有了的取值,我们就可以得到的取值了。
。
直接暴力计算,两个方向转换的时间复杂均为。
FFT
那么 FFT 算法是如何优化计算这一过程的?利用分治。
我们把一个多项式的计算分为偶数项的计算和奇数项的计算:
也就是说, FFT 的思想就是不断得把一个多项式拆分成奇数多项式和偶数多项式,然后合并两个多项式的信息。
也就是说,如果我们已经得到了和,我们只需要就可以得到了。
每次都能把多项式的长度减小一半,于是时间复杂度就是。
模版
C++ 是自带了复数 stl 的,即:
#include
但是常数大,跑得慢,不如自己重载的好。
- 下面的模版必须要保证是的整数次幂。
typedef double LD;
const LD PI = acos(-1);
struct C {
LD r, i;
C(LD r = 0, LD i = 0): r(r), i(i) {}
};
C operator + (const C& a, const C& b) {
return C(a.r + b.r, a.i + b.i);
}
C operator - (const C& a, const C& b) {
return C(a.r - b.r, a.i - b.i);
}
C operator * (const C& a, const C& b) {
return C(a.r * b.r - a.i * b.i, a.r * b.i + a.i * b.r);
}
void FFT(C x[], int n, int p) {
for (int i = 0, t = 0; i < n; ++i) {
if (i > t) swap(x[i], x[t]);
for (int j = n >> 1; (t ^= j) < j; j >>= 1);
}
for (int h = 2; h <= n; h <<= 1) {
C wn(cos(p * 2 * PI / h), sin(p * 2 * PI / h));
for (int i = 0; i < n; i += h) {
C w(1, 0), u;
for (int j = i, k = h >> 1; j < i + k; ++j) {
u = x[j + k] * w;
x[j + k] = x[j] - u;
x[j] = x[j] + u;
w = w * wn;
}
}
}
if (p == -1)
FOR (i, 0, n)
x[i].r /= n;
}
void conv(C a[], C b[], int n) {
FFT(a, n, 1);
FFT(b, n, 1);
FOR (i, 0, n)
a[i] = a[i] * b[i];
FFT(a, n, -1);
}
例题
A * B II
https://acm.ecnu.edu.cn/problem/3007/
大整数相乘。
把每一位都看成是多项式其中一项的系数,那么大数最后的结果也就是多项式乘法系数的结果。
要进位处理。
Hnoi2017 礼物
显然是要计算的最小值,其中$0≤x
展开这个式子,
除了,其他的和与相关的项都可以在的时间内算出了
那么配个方,就可以求出最小值了,而是固定的
现在的问题就是求,我们可以用FFT来解决
如果我们把多项式倒置,我们就能发现式子的和的下标和可以相同,我们可以利用多项式乘法同时算出卷积。
设,那么,这样就可以用FFT算出来了
总的时间复杂度
#include
#define inf 0x3fffffff
using namespace std;
typedef double LD;
const LD PI=acos(-1);
struct C
{
LD r,i;
C(LD r=0,LD i=0):r(r),i(i){}
};
C operator + (const C& a, const C& b){
return C(a.r+b.r,a.i+b.i);
}
C operator - (const C& a, const C& b){
return C(a.r-b.r,a.i-b.i);
}
C operator * (const C& a, const C& b){
return C(a.r*b.r-a.i*b.i,a.r*b.i+a.i*b.r);
}
void FFT(C x[],int n,int p)
{
for (int i=0,t=0;i
-
快速傅立叶变换(FFT)算法实验2012-12-21 0
-
如何使用快速傅立叶变换(FFT)的8590 C/E/L系列频谱分析仪中的FFT函数?2019-04-04 0
-
如何实现傅立叶变换算法?2019-10-08 0
-
浅懂示波器FFT快速傅立叶变换功能及运用2020-01-14 0
-
FFT变换结果的物理意义2021-08-17 0
-
示波器FFT快速傅立叶变换不会用?看完这篇帖子,我彻底悟了2022-09-22 0
-
周期信号的傅立叶变换.ppt2009-09-16 688
-
快速傅立叶变换(FFT)的Nios II实现2010-02-09 904
-
基于FPGA的快速傅立叶变换2009-06-20 978
-
1024点FFT快速傅立叶变换2016-06-07 1060
-
Xilinx 的IP:1024点FFT快速傅立叶变换2016-06-07 1110
-
简述FPGA的快速傅立叶变换2021-05-27 2039
-
傅立叶变换是怎么变换的 傅立叶的理解2021-08-25 4273
-
我印象中的快速傅里叶变换 (FFT)2023-05-05 808
全部0条评论

快来发表一下你的评论吧 !

