

一文详解卡尔曼滤波
描述
作者:嗣音 | 来源:古月居
记录一下对卡尔曼滤波的理解。
卡尔曼滤波(Kalman Filter),以下简称KF,是由Swerling(1958)和Kalman(1960)作为线性高斯系统(linear Gaussian system)中的预测和滤波技术而发明的,是用矩阵来定义的。
KF实现了连续状态的置信度计算。它不适用于离散或混合状态空间。
参考《概率机器人》、《卡尔曼滤波原理及应用-MATLAB仿真》
卡尔曼滤波属于是基于贝叶斯最大后验估计(MAP)的推论。此篇之前所衔接的博客是《概率基础:贝叶斯滤波》。
一、线性高斯系统
1.1 线性系统
线性系统和非线性系统的主要区别在于其输入和输出之间的关系以及其遵循的原理。线性系统相对简单,容易分析和控制,而非线性系统则更复杂,具有更多不确定性和不稳定性。
所谓线性系统即指满足叠加性与齐次性的系统,反之即为非线性系统。
线性系统叠加原理:对于输入信号的线性组合,系统将产生相应的输出信号的线性组合。
线性系统齐次原理:当输入信号放大 k 倍时,输出信号也会放大 k 倍。
平时可以根据这几点判断线性or非线性
1.线性方程是指方程中只包含一次项,而非线性方程则不是这样的形式,可能包含二次、三次或其它次数的项。
2.如果方程中包含有指数或幂,并且指数或幂不等于 1,那么它就是一个非线性方程。
3.如果方程中存在变量与变量的乘积或除法,那么它就是一个非线性方程。
举个例子,2x+3y=5 是一个线性方程,它只包含了一次项;而 x^2+y^2=4 是一个非线性方程,因为它包含了平方项;xy=2 是一个非线性方程,因为它包含了两个变量的乘积。
1.2 高斯分布
高斯分布(Gaussian Distribution)又称正态分布(Normal Distribution)。
若随机变量X服从一个数学期望(均值)为 μ,方差为 σ 的正态分布,则记为 X~N(μ, σ)。
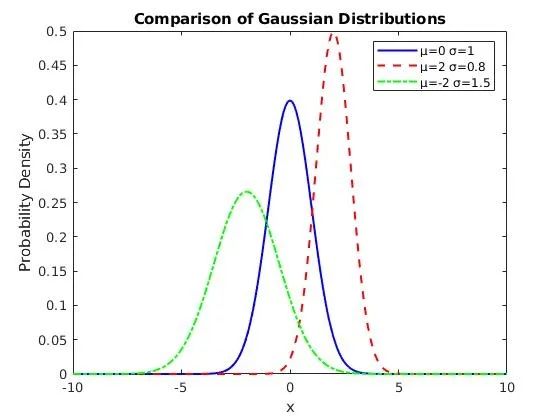
高斯分布的概率密度函数为正态分布,期望值(均值) μ 决定了其位置,其标准差 σ 决定了分布的幅度。
μ = 0、σ = 1;μ = 2、σ = 0.8;μ = -2、σ = 1.5;的分布曲线如下:
matlab代码:
%% 高斯分布(Gaussian Distribution)
% 生成数据点范围
x = -1010;
% 定义不同的高斯分布的均值和标准差
mu1 = 0;
sigma1 = 1;
mu2 = 2;
sigma2 = 0.8;
mu3 = -2;
sigma3 = 1.5;
% 计算不同高斯分布在数据点范围内的概率密度函数值
pdf1 = normpdf(x, mu1, sigma1);
pdf2 = normpdf(x, mu2, sigma2);
pdf3 = normpdf(x, mu3, sigma3);
% 绘制高斯分布曲线
figure;
plot(x, pdf1, 'b-', 'LineWidth', 1.5, 'DisplayName', 'μ=0 σ=1');
hold on;
plot(x, pdf2, 'r--', 'LineWidth', 1.5, 'DisplayName', 'μ=2 σ=0.8');
plot(x, pdf3, 'g-.', 'LineWidth', 1.5, 'DisplayName', 'μ=-2 σ=1.5');
% 添加图例和标签
legend('Location', 'best');
xlabel('x');
ylabel('Probability Density');
title('Comparison of Gaussian Distributions');
grid on;
hold off;
1.3 高维高斯分布
高维高斯分布(Multivariate Gaussian Distribution)又称高维正态分布(Multivariate Normal Distribution)。
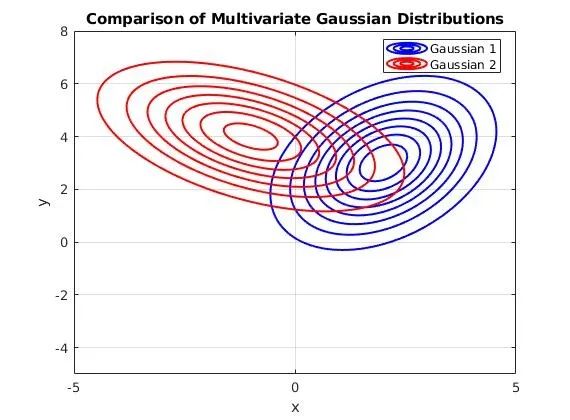
与高斯分布不同的是,其数学期望(均值)为 μ 为一个 1xn 的矩阵,方差这里叫做协方差 cov 为一个 nxn 的矩阵。
μ = [2, 3]、cov = [1.5, 0.7; 0.7, 2.5];μ = [-1, 4]、σ = [3, -1.2; -1.2, 2];的分布曲线如下:
matlab代码:
%% 高维高斯分布(Multivariate Gaussian Distribution)
% 设置均值向量和协方差矩阵
mu1 = [2, 3]; % 第一个高斯分布的均值向量
cov1 = [1.5, 0.7; % 第一个高斯分布的协方差矩阵
0.7, 2.5];
mu2 = [-1, 4]; % 第二个高斯分布的均值向量
cov2 = [3, -1.2; % 第二个高斯分布的协方差矩阵
-1.2, 2];
% 生成数据点范围
x = -55;
y = -58;
% 创建网格数据点
[X, Y] = meshgrid(x, y);
% 将网格数据点组合成行向量
points = [X(:), Y(:)];
% 计算不同高斯分布在数据点范围内的概率密度函数值
pdf1 = mvnpdf(points, mu1, cov1);
pdf2 = mvnpdf(points, mu2, cov2);
% 将概率密度函数值变换回网格形式
PDF1 = reshape(pdf1, size(X));
PDF2 = reshape(pdf2, size(X));
% 绘制高斯分布曲线
figure;
contour(X, Y, PDF1, 'LineColor', 'blue', 'LineWidth', 1.5, 'DisplayName', 'Gaussian 1');
hold on;
contour(X, Y, PDF2, 'LineColor', 'red', 'LineWidth', 1.5, 'DisplayName', 'Gaussian 2');
% 添加图例和标签
legend('Location', 'best');
xlabel('x');
ylabel('y');
title('Comparison of Multivariate Gaussian Distributions');
grid on;
hold off;
1.4 方差与协方差
方差与协方差的理解:
https://zhuanlan.zhihu.com/p/518236536

1.5 线性高斯系统
KF用矩阵参数表示置信度:在时刻t,置信度用均值μ(t)和方差Σ(t)表达。除了贝叶斯滤波的马尔可夫假设(回想隐马尔可夫模型 或 动态贝叶斯网络),还需要具有三个特征,则后验就是高斯的。
1.状态转移概率p(x(t) | u(t), x(t-1))必须是带有随机高斯噪声的参数的线性函数:
x(t) = A(t).x(t-1) + B(t).u(t) + ε(t)
式中,x(t)和x(t-1)为状态向量,其维数为 n ;u(t)为时刻t的控制向量,其维数为 m;A(t)为 n x n 的方阵;B(t)为 n x m的矩阵。
ε(t) 是一个高斯随机向量,表示由状态转移引入的不确定性,其维数与状态向量相同为 n,均值为0,方差用 R(t) 表示。
2.测量概率p(z(t) | x(t))也与带有高斯噪声的自变量呈线性关系:
z(t) = C(t).x(t) + δ(t)
式中,x(t)为状态向量,其维数为 n ;z(t) 为测量向量,其维数为 k ;C(t)为 k x n 的矩阵,均值为0,方差用 Q(t) 表示。
3.初始置信度bel(x0)必须是正态分布的。
二、卡尔曼滤波算法
2.1 算法理解

其推导这里不做记录,可以参照《概率机器人》
使用过程就是这五个黄金公式一直套就对了
1.输入:控制向量u(t)和测量向量z(t);输出:时刻t的置信度,均值为μ(t)和方差为Σ(t)。
2.在第2第3行,计算预测置信度_bel(x(t))的均值_μ(t)和方差为_Σ(t)。
均值利用状态转移函数进行计算,把x(t-1)替换为u(t-1)。
方差是通过线性矩阵A(t)考虑了当前状态依赖前一状态的的事实进行计算的。因为方差是一个二次型的,所以该矩阵两次相乘得到方差。
3.在第4到第6行,通过综合测量z(t)顺序地转换成期望的置信度bel(x(t)).
第4行计算的变量矩阵 K(t) 叫作卡尔曼增益(Kalman gain),它明确了测量综合到新的状态估计的程度。
第5行通过根据卡尔曼增益矩阵K(t)、真实测量向量z(t)的偏差及根据测量方程进行调节来处理均值。
第6行计算后验置信度bel(x(t))的方差,调整由测量引起的信息增益。
2.2 特点描述
1.由于Kalman滤波算法将被估计的信号看作在白噪声作用下一个随机线性系统的输出,并且其输入、输出关系是由状态方程和输出方程在时间域内给出的。
因此这种滤波方法不仅适用于平稳随机过程的滤波,而且特别适用于非平稳或平稳马尔可夫序列的滤波,所以其应用是十分广泛的。
2.Kalman滤波算法是一种时间域滤波的方法,采用状态空间描述系统。
系统的过程噪声和测量噪声并不是需要滤除的对象,它们的统计特性正是估计过程中需要利用的信息,而被估计量和观测量在不同时刻的一、二阶矩却是不必要知道的。
3.由于 Kalman滤波算法的基本方程是时间域内的递推形式,其计算过程是一个不断“预测-修正”的过程。
在求解时不要求存储大量数据,并且一旦观测到了新的数据,随即可以算得新的滤波值,因此这种滤波方法非常适合于实时处理、计算机实现。
4.由于滤波器的增益矩阵与观测无关,因此它可以预先离线算出,从而可以减少实时在线计算量。
在求滤波器增益时,要求一个矩阵的逆,它的阶数只取决于观测方程的维数,而该维数通常很小,这样,求逆运算是比较方便的。
另外,在求解滤波器增益的过程中,随时可以算得滤波器的精度指标 P ,其对角线上的元素就是滤波误差向量各分量的方差。
2.3 噪声矩阵的处理
状态转移方程:x(t) = A(t).x(t-1) + B(t).u(t) + ε(t);观测方程:z(t) = C(t).x(t) + δ(t)
其中我们一般假设,过程噪声 ε(t) 是均值为0方差为 R 的白噪声,观测噪声 δ(t) 是均值为0方差为 Q 的白噪声。
如何确定 R 和 Q 呢?
1.对于过程噪声方差 R
状态转移方程所代表的意义就是:本阶段的状态是上一阶段状态和上一阶段决策的结果。
例如,在目标跟踪系统中,过程噪声往往是路面摩擦力、空气阻力等因素造成的;在温度测量系统中,过程噪声往往是由于人体干扰、阳光照射、风等因素造成的。
要准确获取过程噪声方差 R 比较困难,可以通过对比试验获得。
例如,机器人小车在光滑的玻璃上与粗糙的路面上行驶,两者对比就可以获得在路面上的阻力因素,从而获得过程噪声方差 R。
2.对于观测噪声方差 Q
观测噪声与传感器精度相关。
例如,一个温度计的测量误差是+-1℃;学生用尺子量距离误差是+-1mm;体重计测量体重的误差是+-1g。
根据这类信息,我们可以大致知道他们测量噪声的大小。
一般地,观测噪声的方差 Q 是一个统计意义上的参数:对传感器测量的数据经过长期的概率统计,得到它测量噪声的方差。
三、实例一:温度测量
3.1 问题描述
1.假设我们要研究的对象是一个房间的温度,其温度大概在25℃左右,会小幅度波动,每隔一分钟采样一次,以 t 表达时序。
问题是要通过卡尔曼滤波估算房间真实温度。
这个实例的代表意义是,他是一个一维的线性高斯系统问题。
2.受光照、空气流动影响,真实温度会随环境变化,存在过程噪声。
过程噪声是均值为0、方差 R=0.01的高斯分布;其状态转移方程:x(t) = A(t).x(t-1) + B(t).u(t) + ε(t)
A=1,B=0,ε均值为0、方差R=0.01
3.用温度计测量,误差为+-0.5℃,并从产品说明上得知其方差为0.25,也就是说有测量噪声。
测量噪声是均值为0、方差 Q=0.25的高斯分布;
其观测方程:z(t) = C(t).x(t) + δ(t)
C=1,δ均值为0、方差Q=0.25
3.2 手动解算
假定第 t-1 时刻温度测量值为23.9℃,我们就假设推理到此时刻得到的温度值均值 μ(t-1)=23.9,方差 Σ(t-1)=0.1^2=0.01
假定第 t 时刻温度测量值为24.5℃
首先利用 t-1 时刻的温度值预测第 t 时刻的温度:
预测均值 _μ(t)=μ(t-1)=23.9
预测方差 _Σ(t)=Σ(t-1)+R=0.01+0.01=0.02
计算卡尔曼增益
K=_Σ(t)/(_Σ(t)+Q)=0.02/(0.02+0.25)=0.0741
则此时利用 t 时刻的观测值,得到温度计的估值为:
均值 μ(t)=_μ(t)+K.(z(t)-_μ(t))=23.9+0.0741x(24.5-23.9)=23.915;
方差 Σ(t)=(1-K)*_Σ(t)=(1-0.0741)x0.02=0.018518
后续重复此循环,不断把方差递归
3.3 matlab实现
%% 根据系统描述,初始化一些值
clc;clear;
N = 300; % 采样次数
X = zeros(1,N); % 状态值 真值
Z = zeros(1,N); % 观测值 z(t)
X_kf = zeros(1,N); % kf算法里的状态均值 μ(t)
P_kf = zeros(1,N); % kf算法里的状态方差 Σ(t)
A = 1; % 状态转移方程相关
C = 1; % 测量方程相关
I = eye(1); % 单位矩阵
R = 0.01; % 过程噪声方差
Q = 0.25; % 测量噪声方差
% 初值给定
X(1) = 25.1;
Z(1) = 24.9;
X_kf(1) = Z(1); % 通过第一个观测值来更新初始状态均值 μ(1)
P_kf(1) = 0.01; % 这里直接将过程噪声方差作为初始方差(估摸着)
%% 根据噪声,模拟实际数据 和 测量数据
W = sqrt(R)*randn(1,N); % 过程噪声 ε(t)
V = sqrt(Q)*randn(1,N); % 测量噪声 δ(t)
for t = 2:N
X(t) = A*X(t-1) + W(t-1);
Z(t) = C*X(t) + V(t);
end
%% 卡尔曼滤波
for t = 2:N
X_pre = A*X_kf(t-1); % 预测状态均值 _μ(t)
P_pre = A*P_kf(t-1) + R; % 预测状态方差 _Σ(t)
K = P_pre/(P_pre + Q); % 更新卡尔曼增益 K
X_kf(t) = X_pre + K*(Z(t) - C*X_pre); % 更新状态均值 μ(t)
P_kf(t) = (I - K*C)*P_pre; % 更新状态方差 Σ(t)
end
%% 分析误差项
Err_Messure=zeros(1,N);
Err_Kalman=zeros(1,N);
for t=1:N
Err_Messure(t)=abs(Z(t)-X(t));
Err_Kalman(t)=abs(X_kf(t)-X(t));
end
%% 画图
t=1:N;
figure('Name','Kalman Filter Simulation','NumberTitle','off');
plot(t,X,'-r',t,Z,'-k',t,X_kf,'-g');
legend('real','measure','kalman extimate');
xlabel('sample time (min)');
ylabel('temperature (℃)');
title('Kalman Filter Simulation');
figure('Name','Error Analysis','NumberTitle','off');
plot(t,Err_Messure,'-b',t,Err_Kalman,'-k');
legend('messure error','kalman error');
xlabel('sample time (min)');
ylabel('error (℃)');
title('Error Analysis');
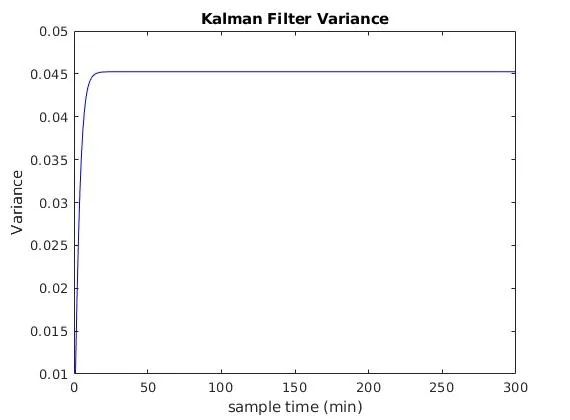
figure('Name','Kalman Filter Variance','NumberTitle','off');
plot(t,P_kf,'-b');
xlabel('sample time (min)');
ylabel('Variance');
title('Kalman Filter Variance');
3.4 结果分析
真实值、测量值、KF得到的值如下,可以看到明显的效果。
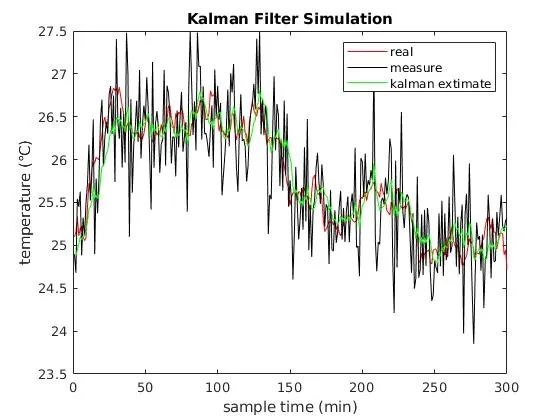
测量值、KF得到的值与真实值做差对比如下。
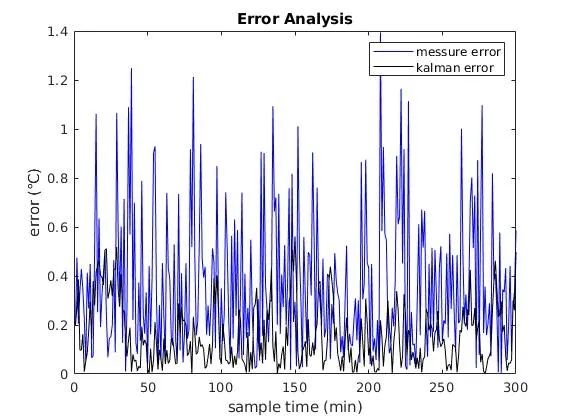
这个一维高斯分布里,其方差也是一维了,我们可以看到随着观测数据的积累和滤波器的逐渐收敛方差趋于稳定。
四、实例二:自由落体运动目标跟踪
4.1 问题描述
1.某一物体在重力作用下自由落体,有观测装置对其进行检测,采样间隔1s。
需要估计该物体的运动位移 x 和速度 v。
这个实例的代表意义是,它只有一个观测,但解决的是一个2维的状态估计问题.
2.根据运动学方程,该物体的状态转移方程为:
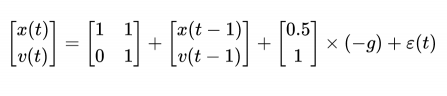
ε(t) = [0]T 也即过程噪声为高斯分布,其均值为0、方差 R = [0]T ,物体的初始状态为 [95, 1]T,初始方差为 [sqrt(100), 0; 0 ,sqrt(1)]
3. 给定观测装置,在测量时受到随机干扰 δ(t) 影响,其方差为测量噪声 Q = [1]T,观测方程写为:
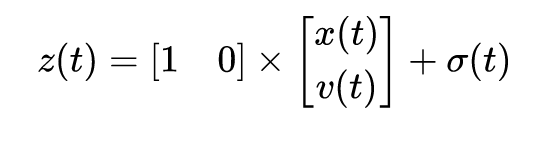
4.2 手动解算
略,看matlab代码及注释。
4.3 matlab实现
printf("hello world!");
4.4 结果分析
真实值、测量值、KF得到的值如下,因为值比较大,所以这里不是很能看出什么。
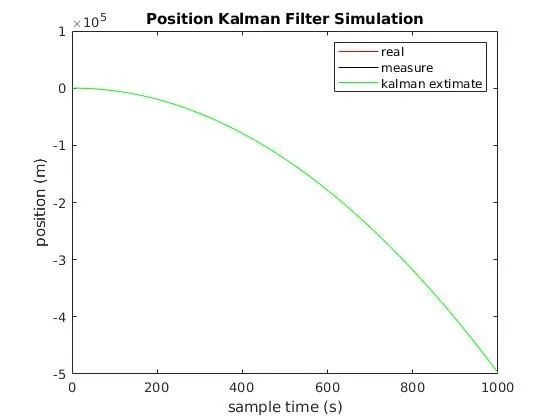
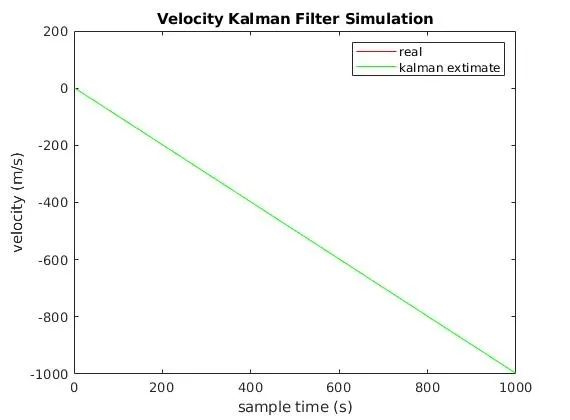
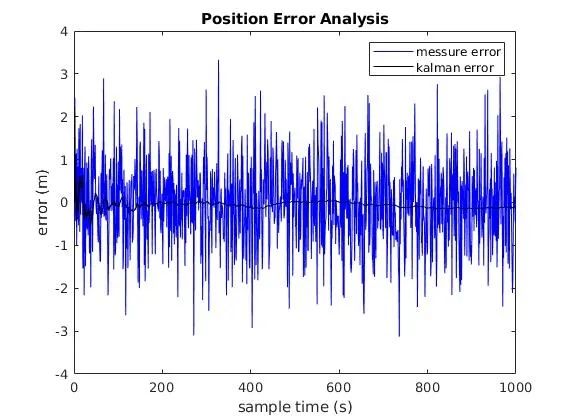
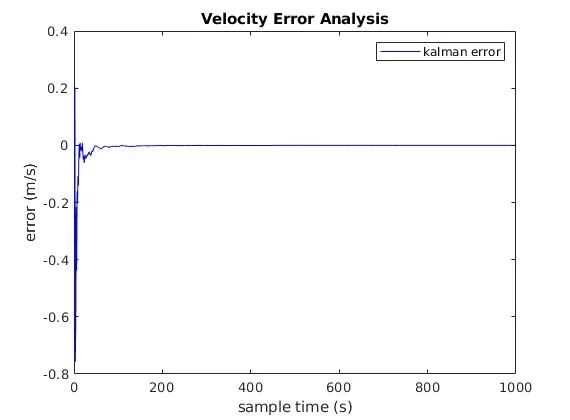
测量值、KF得到的值与真实值做差对比如下,这个就能比较明显的效果了。
五、实例三:船舶GPS导航定位系统
5.1 问题描述
1.船舶出港沿着某直线方向航行,采样间隔∆t。
需要估计船在x和y方向上的位置和速度为x(t)、vx(t)、y(t)、vy(t)
这个实例的代表意义是,它只有一个观测,但解决的是一个4维的状态估计问题。
2.船舶动力系统的控制信号u(t)是人为输出的已知机动信号;过程噪声则来自于由海浪和海风引起的随机加速度。
这里不考虑船自身的动力因素,也就是假设 u(t)=0。
过程噪声ε(t)为高斯分布,其均值为0、方差为 R 。
根据运动学方程,该物体的状态转移方程为:
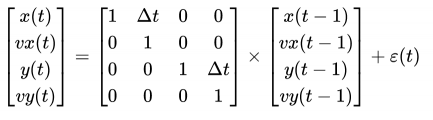
3. 给定GPS观测装置观测位置,民用GPS导航卫星播放的信号人为加入了高频震荡随机干扰信号。
将干扰信号看做观测噪声δ(t),假设其为零均值、方差为 Q 的白噪声。
观测方程写为:
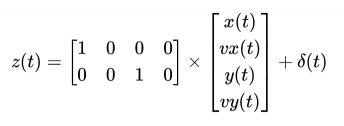
5.2 手动解算
略,看matlab代码及注释。
5.3 matlab实现
%% 根据系统描述,初始化一些值
clc;clear;
T = 1; % 采样步长 ∆t
N = 80/T; % 采样次数
X = zeros(4,N); % 状态值X=[x y vx vy]T 真值
Z = zeros(2,N); % 观测值Z=[Zx Zy]
R = (1e-2)*diag([0.5,1,0.5,1]); % 过程噪声方差,diag对角矩阵
Q = 100*eye(2); % 测量噪声方差
A =[1,T,0,0; % 状态转移方程相关
0,1,0,0;
0,0,1,T;
0,0,0,1];
C = [1,0,0,0; % 测量方程相关
0,0,1,0];
I = eye(4); % 单位矩阵
X_kf = zeros(4,N); % kf算法里的状态均值 μ(t)
P_kf = zeros(4,4,N); % kf算法里的状态方差 Σ(t)
Xkf = X_kf;
F=A;
H=C;
% 初值给定
X(:,1) = [-100,2,200,20];
Z(:,1) = [X(1,1),X(3,1)];
X_kf(:,1) = X(:,1);
P_kf(:,:,1) = eye(4);
%% 根据噪声,模拟实际数据 和 测量数据
for t = 2:N
X(:,t) = A*X(:,t-1) + sqrtm(R)*randn(4,1);
Z(:,t) = C*X(:,t) + sqrtm(Q)*randn(2,1);
end
%% 卡尔曼滤波
P0 = eye(4);
for t=2:N
X_pre = A*X_kf(:,t-1);
P_pre = A*P_kf(:,:,t-1)*A' + R;
K = P_pre*C'/(C*P_pre*C' + Q);
X_kf(:,t) = X_pre + K*(Z(:,t) - C*X_pre);
P_kf(:,:,t) = (eye(4) - K*C)*P_pre;
end
%% 分析误差项
Err_Messure_x = zeros(1,N);
Err_Kalman_x = zeros(1,N);
Err_Kalman_v = zeros(1,N);
for t = 1:N
Err_Messure_x(t) = RMS(X(:,t),Z(:,t)); % RMS:自定义函数,求欧拉距离的
Err_Kalman_x(t) = RMS(X(:,t),X_kf(:,t));
end
%% 画图
t=1:N;
figure('Name','Kalman Filter Simulation','NumberTitle','off');
plot(X(1,:),X(3,:),'-k',Z(1,:),Z(2,:),'-b.',X_kf(1,:),X_kf(3,:),'-r+');
legend('real','measure','kalman extimate');
xlabel('position x (m)');
ylabel('position y (m)');
title('Kalman Filter Simulation');
figure('Name','Error Analysis','NumberTitle','off');
plot(t,Err_Messure_x,'-g.',t,Err_Kalman_x,'-r.');
legend('messure error','kalman error');
xlabel('sample time (s)');
ylabel('error (m)');
title('Error Analysis');
% 在MATLAB中,您可以使用 plot 函数来绘制线条和散点图,但是不能将多个数据集的线条和散点图组合在一起绘制。
% 如果您想绘制两个数据集的线条和散点图,请使用两个独立的 plot 函数调用来绘制它们
% figure
% hold on; box on;
% plot(Err_Messure_x,'-ko','MarkerFace','g')
% plot(Err_Kalman_x,'-ks','MarkerFace','r')
% legend('messure error','kalman error')
%% 自定义函数,求欧拉距离的: d = sqrt(∆x^2 + ∆y^2)
function dist=RMS(X1,X2)
if length(X2)<=2
dist=sqrt( (X1(1)-X2(1))^2 + (X1(3)-X2(2))^2 );
else
dist=sqrt( (X1(1)-X2(1))^2 + (X1(3)-X2(3))^2 );
end
end
5.4 结果分析
真实值、测量值、KF得到的值如下,可以看到明显的效果。
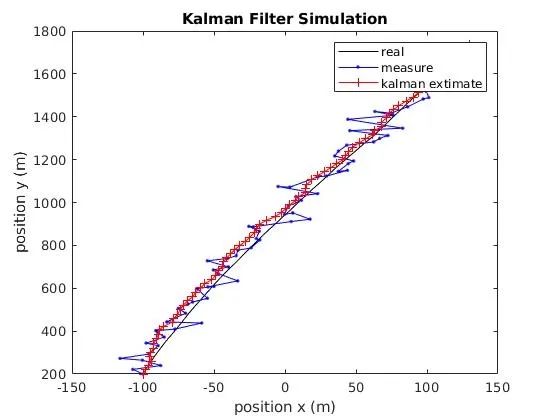
测量值、KF得到的值与真实值做差对比如下。
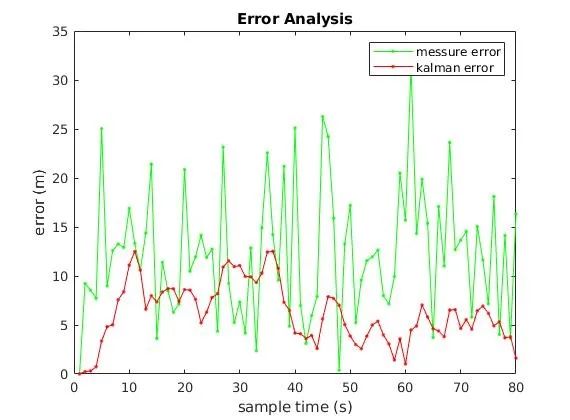
-
卡尔曼滤波器介绍2008-07-14 0
-
卡尔曼滤波2013-07-04 0
-
图书分享:卡尔曼滤波算法的几何解释2015-06-11 0
-
卡尔曼滤波的原理说明2016-09-21 0
-
卡尔曼滤波算法2017-03-23 0
-
LabVIEW一维卡尔曼滤波算法2017-10-21 0
-
卡尔曼滤波的原理及如何实现2020-06-01 0
-
卡尔曼滤波有哪些应用2021-07-12 0
-
卡尔曼滤波器的使用原理2021-08-17 0
-
卡尔曼滤波C代码2021-08-17 0
-
卡尔曼滤波器是什么2021-11-16 0
-
卡尔曼滤波简介2022-02-28 0
-
卡尔曼滤波是属于一个什么滤波器?2023-10-11 0
-
详解卡尔曼滤波原理2023-07-13 1812
全部0条评论

快来发表一下你的评论吧 !

