

浅谈SMOTE算法 如何利用Python解决非平衡数据问题
嵌入式技术
描述
好久没有更新自己写的文章了,相信很多读者都会比较失望,甚至取关了吧,在此向各位网友道个歉。文章未及时更新的主要原因是目前在写Python和R语言相关的书籍,激动的是基于Python的数据分析与挖掘的书已经编写完毕,后期还继续书写R语言相关的内容。希望得到网友的理解,为晚来的新文章再次表示抱歉。
本次分享的主题是关于数据挖掘中常见的非平衡数据的处理,内容涉及到非平衡数据的解决方案和原理,以及如何使用Python这个强大的工具实现平衡的转换。
SMOTE算法的介绍
在实际应用中,读者可能会碰到一种比较头疼的问题,那就是分类问题中类别型的因变量可能存在严重的偏倚,即类别之间的比例严重失调。如欺诈问题中,欺诈类观测在样本集中毕竟占少数;客户流失问题中,非忠实的客户往往也是占很少一部分;在某营销活动的响应问题中,真正参与活动的客户也同样只是少部分。
如果数据存在严重的不平衡,预测得出的结论往往也是有偏的,即分类结果会偏向于较多观测的类。对于这种问题该如何处理呢?最简单粗暴的办法就是构造1:1的数据,要么将多的那一类砍掉一部分(即欠采样),要么将少的那一类进行Bootstrap抽样(即过采样)。但这样做会存在问题,对于第一种方法,砍掉的数据会导致某些隐含信息的丢失;而第二种方法中,有放回的抽样形成的简单复制,又会使模型产生过拟合。
为了解决数据的非平衡问题,2002年Chawla提出了SMOTE算法,即合成少数过采样技术,它是基于随机过采样算法的一种改进方案。该技术是目前处理非平衡数据的常用手段,并受到学术界和工业界的一致认同,接下来简单描述一下该算法的理论思想。
SMOTE算法的基本思想就是对少数类别样本进行分析和模拟,并将人工模拟的新样本添加到数据集中,进而使原始数据中的类别不再严重失衡。该算法的模拟过程采用了KNN技术,模拟生成新样本的步骤如下:
采样最邻近算法,计算出每个少数类样本的K个近邻;
从K个近邻中随机挑选N个样本进行随机线性插值;
构造新的少数类样本;
将新样本与原数据合成,产生新的训练集;
为了使读者理解SMOTE算法实现新样本的模拟过程,可以参考下图和人工新样本的生成过程:
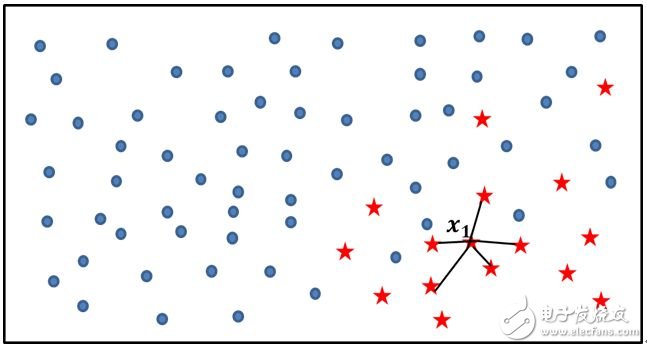
如上图所示,实心圆点代表的样本数量要明显多于五角星代表的样本点,如果使用SMOTE算法模拟增加少类别的样本点,则需要经过如下几个步骤:
利用KNN算法,选择离样本点x1最近的K个同类样本点(不妨最近邻为5);
从最近的K个同类样本点中,随机挑选M个样本点(不妨M为2),M的选择依赖于最终所希望的平衡率;
对于每一个随机选中的样本点,构造新的样本点;新样本点的构造需要使用下方的公式:

其中,xi表示少数类别中的一个样本点(如图中五角星所代表的x1样本);xj表示从K近邻中随机挑选的样本点j;rand(0,1)表示生成0~1之间的随机数。
假设图中样本点x1的观测值为(2,3,10,7),从图中的5个近邻中随机挑选2个样本点,它们的观测值分别为(1,1,5,8)和(2,1,7,6),所以,由此得到的两个新样本点为:

重复步骤1)、2)和3),通过迭代少数类别中的每一个样本xi,最终将原始的少数类别样本量扩大为理想的比例;
通过SMOTE算法实现过采样的技术并不是太难,读者可以根据上面的步骤自定义一个抽样函数。当然,读者也可以借助于imblearn模块,并利用其子模块over_sampling中的SMOTE“类”实现新样本的生成。有关该“类”的语法和参数含义如下:

ratio:用于指定重抽样的比例,如果指定字符型的值,可以是’minority’,表示对少数类别的样本进行抽样、’majority’,表示对多数类别的样本进行抽样、’not minority’表示采用欠采样方法、’all’表示采用过采样方法,默认为’auto’,等同于’all’和’not minority’;如果指定字典型的值,其中键为各个类别标签,值为类别下的样本量;
random_state:用于指定随机数生成器的种子,默认为None,表示使用默认的随机数生成器;
k_neighbors:指定近邻个数,默认为5个;
m_neighbors:指定从近邻样本中随机挑选的样本个数,默认为10个;
kind:用于指定SMOTE算法在生成新样本时所使用的选项,默认为’regular’,表示对少数类别的样本进行随机采样,也可以是’borderline1’、’borderline2’和’svm’;
svm_estimator:用于指定SVM分类器,默认为sklearn.svm.SVC,该参数的目的是利用支持向量机分类器生成支持向量,然后再生成新的少数类别的样本;
n_jobs:用于指定SMOTE算法在过采样时所需的CPU数量,默认为1表示仅使用1个CPU运行算法,即不使用并行运算功能;
分类算法的应用实战
本次分享的数据集来源于德国某电信行业的客户历史交易数据,该数据集一共包含条4,681记录,19个变量,其中因变量churn为二元变量,yes表示客户流失,no表示客户未流失;剩余的自变量包含客户的是否订购国际长途套餐、语音套餐、短信条数、话费、通话次数等。接下来就利用该数据集,探究非平衡数据转平衡后的效果。



如上图所示,流失用户仅占到8.3%,相比于未流失用户,还是存在比较大的差异的。可以认为两种类别的客户是失衡的,如果直接对这样的数据建模,可能会导致模型的结果不够准确。不妨先对该数据构建随机森林模型,看看是否存在偏倚的现象。
原始数据表中的state变量和Area_code变量表示用户所属的“州”和地区编码,直观上可能不是影响用户是否流失的重要原因,故将这两个变量从表中删除。除此,用户是否订购国际长途业务international_plan和语音业务voice_mail_plan,属于字符型的二元值,它们是不能直接代入模型的,故需要转换为0-1二元值。


如上表所示,即为清洗后的干净数据,接下来对该数据集进行拆分,分别构建训练数据集和测试数据集,并利用训练数据集构建分类器,测试数据集检验分类器:


如上结果所示,决策树的预测准确率超过93%,其中预测为no的覆盖率recall为97%,但是预测为yes的覆盖率recall却为62%,两者相差甚远,说明分类器确实偏向了样本量多的类别(no)。


如上图所示,ROC曲线下的面积为0.795,AUC的值小于0.8,故认为模型不太合理。(通常拿AUC与0.8比较,如果大于0.8,则认为模型合理)。接下来,利用SMOTE算法对数据进行处理:


如上结果所示,对于训练数据集本身,它的类别比例还是存在较大差异的,但经过SMOTE算法处理后,两个类别就可以达到1:1的平衡状态。下面就可以利用这个平衡数据,重新构建决策树分类器了:

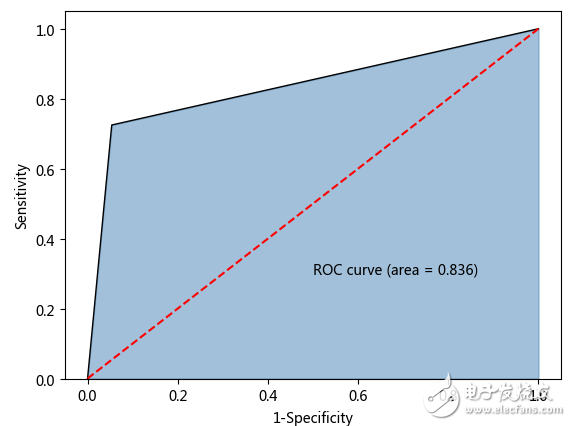
如上结果所示,利用平衡数据重新建模后,模型的准确率同样很高,为92.6%(相比于原始非平衡数据构建的模型,准确率仅下降1%),但是预测为yes的覆盖率提高了10%,达到72%,这就是平衡带来的好处。


最终得到的AUC值为0.836,此时就可以认为模型相对比较合理了。
-
Python建模算法与应用2024-07-24 1743
-
如何利用Python和pandas来处理json数据2023-11-01 3585
-
基于Python实现随机森林算法2023-09-21 2321
-
[源代码]Python算法详解2023-06-06 598
-
Python实现所有算法-基本牛顿法2022-07-13 2155
-
基于Borderline-SMOTE和双Attention的入侵检测2021-04-08 931
-
Python的Apriori算法和FP-Growth算法是什么2020-06-04 1577
-
如何利用Python进行数据分析2020-04-23 2462
-
利用Python进行数据分析之时间序列基础2020-03-20 1143
-
Python的分类数据2019-10-31 2347
-
利用python实现KNN算法2019-10-25 1559
-
白平衡几种算法总结2018-01-17 23508
-
基于主动学习不平衡多分类AdaBoost改进算法2017-11-30 979
-
利用仪表放大器解决非常规设计问题2011-11-28 648
全部0条评论

快来发表一下你的评论吧 !

