

机器学习中低精度计算产生高准确度结果的解决方案
电子说
描述
有人认为,用低精度训练机器学习模型会限制训练的精度,事实真的如此吗?本文中,斯坦福大学的DAWN人工智能研究院介绍了一种名为bit recentering的技术,它可以用低精度的计算实现高准确度的解决方案。以下是论智对原文的编译,文末附原论文地址。
低精度计算在机器学习中已经吸引了大量关注。一些公司甚至已经开始研发能够原生支持并加速低精度操作的硬件了,比如微软的脑波计划(Project Brainwave)和谷歌的TPU。虽然使用低精度计算对系统来说有很多好处,但是低精度方法仍然主要用于推理,而非训练。此前,低精度训练算法面临着一个基本困境(fundamental tradeoff):当使用较少的位进行计算时,舍弃误差就会增加,这就限制了训练的准确度。根据传统观点,这种制约限制了研究人员在系统中部署低精度训练算法的能力,但是这种限制能否改变?是否有可能设计一种使用低精度却不会限制准确度的算法呢?
答案是肯定的。在某些情况下我们可以从低精度训练中获得高准确度的解决方案,在这里我们使用了一种新的随机梯度下降方法,称为高准确度低精度(HALP)法。HALP比之前的算法表现更好,因为它减少了两个限制低精度随机梯度下降准确度的噪声源:梯度方差和舍弃误差。
为了减少梯度方差带来的噪音,HALP使用常见的SVRG(stochastic variance-reduced gradient)技术。SVRG能定期使用完全梯度来减少随机梯度下降中使用的梯度样本的方差。
为了降低量化数字带来的噪声,HALP使用了名为“bit centering”的新技术,它背后的原理是,当我们接近最优点时,梯度渐变的幅度变小。也就是说携带的信息变少,于是我们能对其进行压缩。通过动态地重新调整低精度数字,我们可以在算法收敛时降低量化噪声。
将这两种技术结合,HALP能够以和全精度SVRG同样的线性收敛率生成任意准确地解决方案,同时在低精度迭代时使用的是固定位数。这个结果颠覆了有关低精度训练算法的传统观点。
为什么低精度的随机梯度下降有所限制?
首先先交代一下背景:我们想要解决以下这个训练问题:
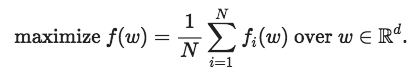
这是用来训练许多机器学习模型(包括深度神经网络)的经典实证问题:让风险最小化。解决这个问题的标准方法之一是随机梯度下降,它是一种通过运行接近最佳值的迭代算法。
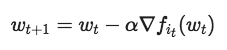
在每次迭代时,it是从{1,..., N}中随机挑选的一个指数,我们虽然想运行这样的算法,但是要保证迭代wt是低精度的。也就是说,我们希望它们使用较少位的定点运算(通常为8位或16位)。但是,当直接对随机梯度下降更新规则而进行这项操作时,我们遇到了问题:问题的解决方案w可能无法再选中的定点表示中显示出来。例如,如果一个8位的定点表示,可以储存{-128,-127,…,127}之间的整数,正确的解决方法是w*=100.5,那么我们与解决方案的距离不可能小于0.5,因为我们不能表示非整数。除此之外,将梯度转换为定点导致的舍弃误差可能会减慢收敛速度,这也影响了低精度SGD的准确性。
Bit Centering
当我们运行随机梯度下降时,在某种意义上,我们世纪正对一堆梯度样本进行平均(或总结)。Bit Centering背后的关键思想是随着梯度渐变逐渐变小,我们可以用同样的位数、以较小的误差对它们求平均值。想要知道为什么,想像一下,你想对[-100, 100]之间的数字求平均值,然后和[-1, 1]的平均值作比较。在前一个集合中,我们需要选择一个定点表示,它可以覆盖整个集合(例如{-128,-127,…,127})。而在第二个集合中,我们选择的定点要覆盖[-1, 1],例如{-128/127,-127/127,..., 126/127,127/127}。这就意味着在固定位数情况下,第二种情况中的相邻可表示数字之间的差值比第一种情况更小,因此舍弃误差也更低。
这个关键的想法让我们得到了启发。为了在[-1, 1]中求出比[-100, 100]中更少误差的平均数,我们需要用一个不同的定点表示,即我们应该不断更新低精度表示:随着梯度渐变得越小,我们应该用位数更小的定点数字,覆盖更小的范围。
但是我们该如何更新表示呢?我们要覆盖的范围到底多大?如果目标是带有参数μ的强凸,那么不管我们何时在某一点w采取完整的梯度渐变是,都可以用以下公式限制最佳位置
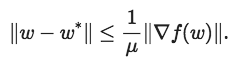
这种不等式为最终的解决方案提供了一系列可能的定位,所以无论何时计算完整梯度,我们都可以重新居中并缩放低精度表示以覆盖此范围。下图说明了这一过程。
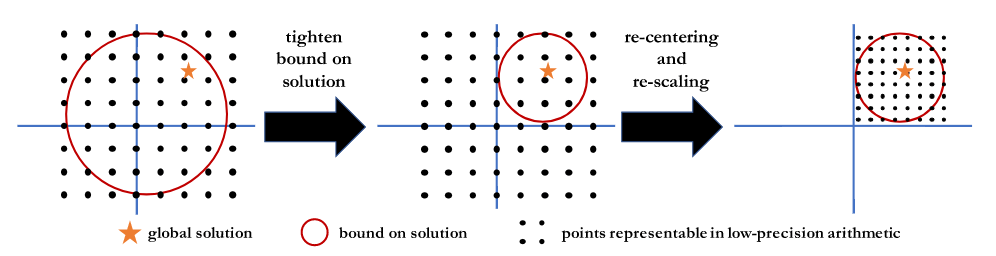
HALP
HALP是运行SVRG并在每个时期都使用具有完全梯度的bit centering更新低精度表示的算法。原论文有对这一方法的具体描述,在这里我们只简单做些介绍。首先,我们证明了,对于强凸的Lipschitz光滑函数,只要我们使用的位数b满足
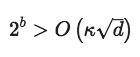
其中κ是该问题的条件数字,那么为了适当设置尺寸和时间长度,HALP将以线性速度收敛到任意准确度的解。更显然的是,0<γ<1,
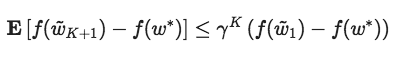
其中wk+1表示第K次迭代后的值。下表表现了这一变化过程
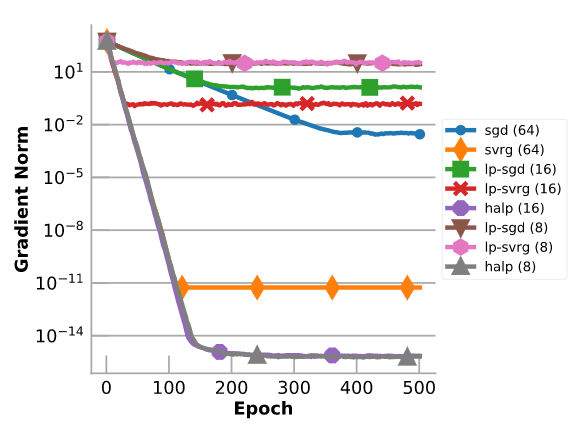
图表通过对具有100个特征和1000个样本的合成数据集进行线性回归,来评估HALP。将它与全精度梯度下降、SVRG、低精度的梯度下降和低精度的SVRG进行比较。需要注意的是,尽管只有8位(受到浮点错误的限制),HALP仍能收敛到精度非常高的结果上。在这种情况下,HALP可以比全精度SVRG收敛到更高精度的结果中,因为HALP较少使用浮点运算,因此对浮点的非准确性不敏感。
- 相关推荐
- 机器学习
-
如何用ADUC845产生高准确度的脉冲?2024-01-11 0
-
高准确度温度***可调报警信号2012-08-14 0
-
焊咀温度测量及影响测量准确度的因素2017-07-28 0
-
数字万用表的准确度如何表示?2017-11-30 0
-
准确度、精密度和精确度2018-02-08 0
-
贴装的准确度、精密度和分辨率的简介与区别2018-09-05 0
-
请问要达到0.05%的测量精度需要多少位分辨率和准确度的ADC?2018-09-13 0
-
SMD校准结果准确度如何2019-02-12 0
-
请问F28335的AD采样频率与准确度是怎么变化的?2020-06-09 0
-
影响焊接测量准确度的因素有哪些2020-09-04 0
-
机器学习实战:GNN加速器的FPGA解决方案2020-10-20 0
-
什么是准确度/精确度?2021-01-25 0
-
在0.01的超低功率因数下,功率分析仪功率测量可以达到多高的准确度呢?2021-03-22 0
-
如何去设计高准确度可程控延迟快前沿脉冲信号源系统?2021-04-20 0
-
请问要达到0.05%的测量精度,需要多少位分辨率和准确度的ADC?2023-12-18 0
全部0条评论

快来发表一下你的评论吧 !

