

MNIST是一个简单的计算机视觉数据集
电子说
描述
从某种程度上来说,没有人真正理解机器学习。
这不是一个复杂的问题,我们所做的一切也都非常简单,但由于一些天生的“障碍”,我们人类确实难以理解发生在计算机“大脑”中的那些简单事物。
人类长久以来的生理进化决定了我们能推理二维、三维的空间,在这基础上,我们也能靠想象思考四维空间里发生的变化。但这对于机器学习来说却是小巫见大巫,它通常需要处理数千、数万,甚至数百万个维度!即便是很简单的问题,如果我们把它放进维度非常高的空间内来解决,以人类的目前的大脑,不理解也不足为奇。
因此,直观地感受高维空间是没有希望的。
为了在高维空间中做一些事情,我们建立了许多工具,其中一个庞大的、发达的分支是降维,它探索的是把高维数据转换为低维数据的技术,也为此做了大量可视化方面的工作。
所以如果我们希望可视化机器学习、深度学习,这些技术会是我们必备的基础知识。可视化意味着我们能更直观地感受实际正在发生的事情,我们也可以借此更深入地了解神经网络。为了这一目的,我们要做的第一件事是理解降维,我们选择的数据集是MNIST。
MNIST
MNIST是一个简单的计算机视觉数据集,它由28×28像素的手写数字图像组成,例如:
每个MNIST数据点,每个图像,都可以被看作是描述每个像素有多暗的数字数组。例如我们可以这么看待这个手写数字“1”:
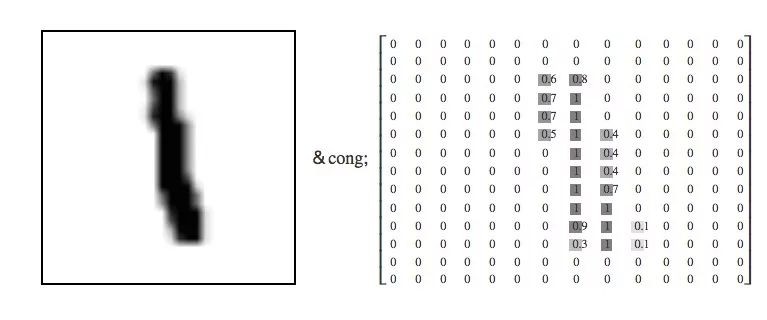
因为每个图像的像素都是28×28,所以我们得到的其实是一个28×28的矩阵。考虑到矢量的每个分量都是介于0和1之间的一个描述明暗程度的值,如果我们把每一个值都看做是维向量,那这就是一个28×28=784的高维空间。
所以空间内的矢量其实并不都是MNIST数字,不同像素点之间的区别称得上是天差地别。为了论证这一点,我们从图像中随机选取了几个点并把它们放大——这是个像素为28×28的图像——每个像素的颜色可能是黑色的、白色的或带阴影灰色的。如下图所示,选取的随机点看起来更像是噪声。

像MNIST数字这样的图像是非常罕见的,虽然数据点被嵌入在784维空间中,但它们又被包含在一个非常小的子空间内。用更复杂的话说,就是它们占据较低维的子空间。
人们对MNIST数字占据的子空间维数具体是多少有很多讨论,其中流行在机器学习研究人员中的一个假设是流形理论:MNIST是一个低维流形结构,高维数据通过它嵌入高维空间中,形成扫掠和弯曲。而与拓扑数据分析更相关的另一个假设是,像MNIST数字这样的数据具有一些触手状的突起,这些突起会嵌入周围空间中。
但是事实究竟是什么,没有人真正知道!
MNIST立方体
为了探索这一点,我们可以把MNIST数据点看作是在一个784维立方体中固定的一点。立方体的每个维度都对应一个特定的像素,根据像素强度,数据点的范围在0到1之间。在维度的一边,是像素为白色的图像,在另一边,是像素为黑色的图像。在它们之间的是灰色图像。
如果这样想,一个自然而然的问题是如果我们只看到一个特定的二维面,那这个立方体看起来会是什么样的?就像盯着一个雪球,我们只能看到投影在二维平面上的数据点,一个维度对应像素强度,另一个维度对应另一个像素。这样做能帮助我们用原始的方式探索MNIST。
在下图中,每个点都表示一个MNIST数据点,颜色表示所属类别(哪个数字)。当我们把鼠标放在上面后,它的图像会出现在各个轴上。每个轴对应特定的像素明暗强度。

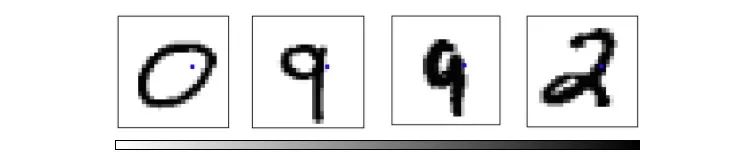
探索这个可视化有助于我们挖掘MNIST结构的一些信息。如下图所示,如果选取坐标为p18,16和p7,12的像素,数字0会聚集在右下角,数字9则会集中在左上角。

红色点为0,粉色点为9
如果选取坐标为p5,6和p7,9处的像素,那数字2会大量出现在右上角,数字3则集中在右下角。

黄绿色点为2,绿色点为3
这看似是个小小的进步,但我们其实不可能完全以这种方式理解MNIST。这些小发现有时并没什么说服力,它们更像是运气的产物,虽然我们从中窥见的关于结构的信息量很少,但这种思维方式是正确的。如果我们从平面看不到理想的数据结构,那我们也许能从某个角度来观察这些数据。
这就牵出了第二个问题,我们该怎么选择合适的角度。平行看数据时,我们该转动几度;垂直看数据时,我们又该怎么扭?好在这个难题已经有人帮我们解决了——主成分分析(PCA)。比起手动计算,PCA将会找到最多的角度(捕捉尽可能多的变化)。
从一个角度看784维的立方体意味着我们要确定立方体每个轴的倾斜方向:是向这边、向那边。还是两头向中间。具体来说,以下是PCA选出的两个角度的图片,红色表示像素的尺寸向一侧倾斜,蓝色则表示向另一侧倾斜。
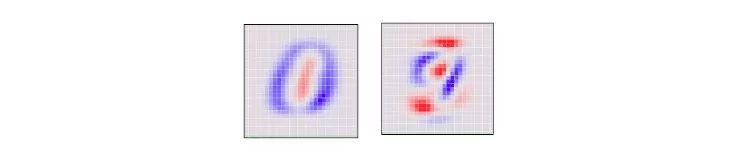
如果MNIST数字基本呈现红色,它就在对应的一侧结束,反之亦然。我们选择PCA选择的第一个“主要成分”作为水平角度,然后再把“大部分红色小部分蓝色”的点推向左侧,把“大部分蓝色小部分红色”的点推向右侧。
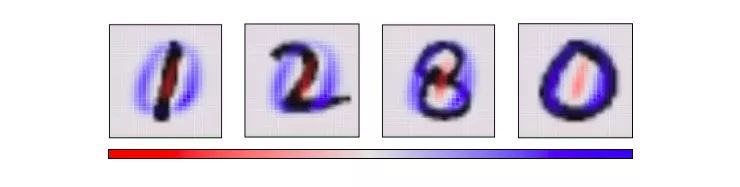
现在我们知道最佳的水平和垂直角度,我们可以尝试从这个角度来观察立方体。
下图和之前的可视化动图基本类似,不同的是它把两个轴固定为第一个“主成分”和第二个“主成分”,也就是我们观察数据的角度。在每个轴上的图像中,蓝色和红色表示的是该像素的不同“倾向”。
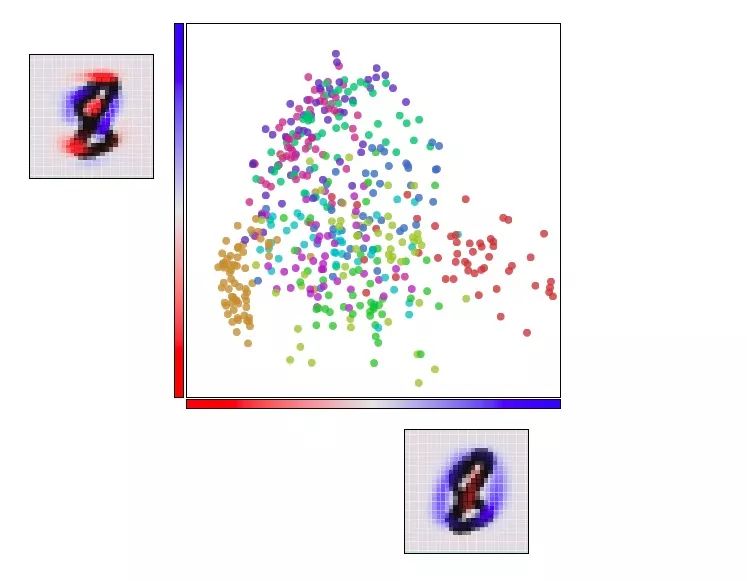
用PCA可视化MNIST
虽然效果更好了,但它还称不上是完美的,因为即便从最好的角度观察,MNIST的数据也不能很好地排列。这是个很特别的高维解构,简单的线性变换还不能分解其中的复杂性。
值得庆幸的是,我们有一些强大的工具来处理这类“不友好”的数据集。
基于优化的降维
这里我们再明确一下可视化的目的——我们为什么要追求“完美”的可视化?可视化的目标又该是什么?
如果在可视化图像中,数据点之间的距离和它们在原高维空间中的距离相同,那这就是个理想的结果。因为做到了这点,就意味着我们已经捕捉到了数据的全局分布。
更准确地说,对于MNIST图像中的任意两个数据点xi和xj,它们之间有两种距离,一种是在原空间中的距离d∗i,j,另一种则是在可视化图像中的欧式距离di,j。它们之间的cost是:
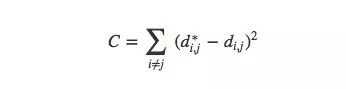
这个值是衡量可视化是好是坏的标准:只要距离不相同,那这就是个不好的可视化。如果C值过大,这意味着可视化图像中的距离和原距离很不一样;如果C值很小,这说明两者十分相近;如果C值为0,我们就得到了一个“完美”的嵌入。
这听起来就像一个优化问题了!相信任何一个深度学习研究人员都知道该怎么做——选取一个随机点并使用梯度下降。

用MDS可视化MNIST
这种方法被称为多维缩放(MDS)。首先,我们把每个点随机放在一个平面上,用一个长度等于原始距离d∗i,j的“弹簧”把点与点连接起来,随着点在空间中自由移动,这个“弹簧”能依靠物理把新距离控制在可控范围内。
当然,事实上这个cost是不会等于0的,因为在控制距离不变的情况下把高维空间嵌入二位空间是不可能的,我们也需要这种不可能。虽然还有些缺陷,但从上图中我们可以看到,这些数据点已经显示出了聚类趋势,这是个进步不小的可视化。
Sammon映射
为了更尽善尽美,这里我们再引入MDS的一个变体——Sammon映射。首先要声明一点,就是MDS有很多变体,而且它们的共同特征是认为cost函数强调数据的局部结构比整体结构更重要。当采用中心化的内积计算邻近矩阵时,我们希望原始距离和主成分是相等的,为了捕捉更多可能性,Sammon映射的做法是保护较小的距离。
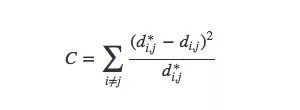
如下图所示,比起关注距离较远两点的位置,Sammon映射更关注附近点的距离控制,如果说某两个点原距离是其他两点的二分之一,那它们被“重视”的程度会是后者的两倍。
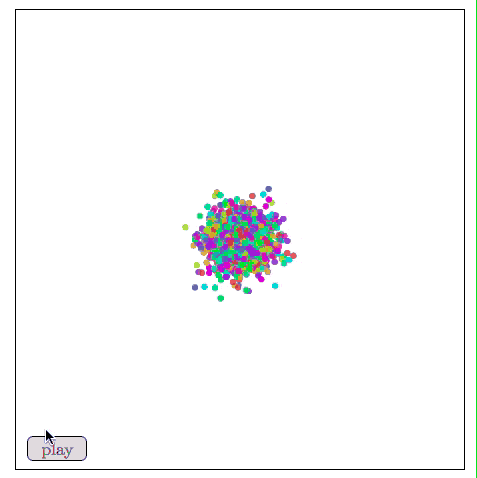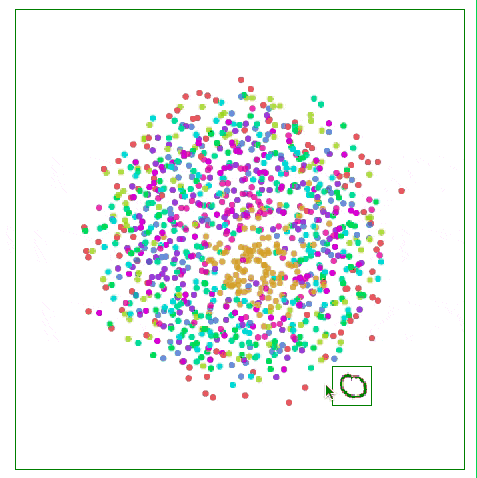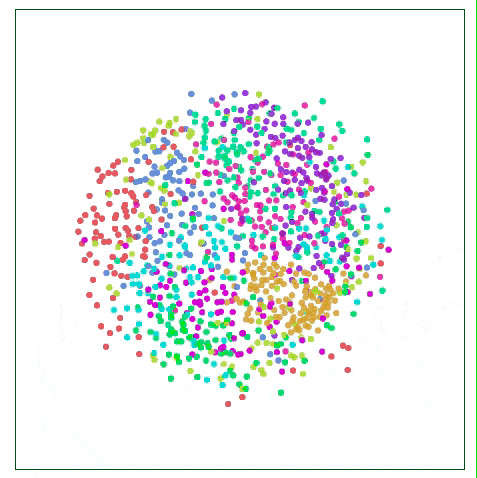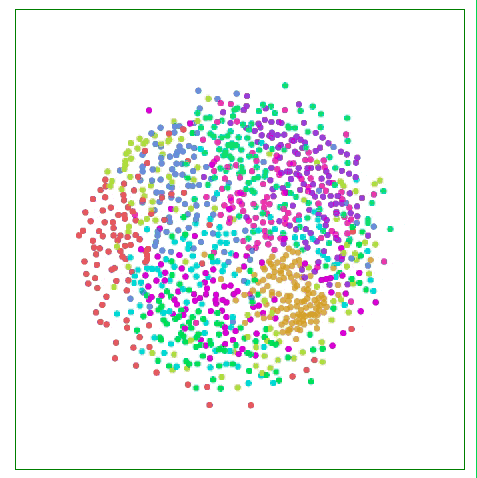
用Sammon映射可视化MNIST
对于MNIST,这种方法并没有显示出太大的不同,这是因为高维空间中数据点的距离不够直观,例如MNIST中的相同数字“1”之间的距离:
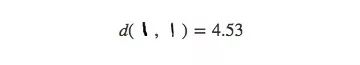
或者不同的数字“9”和“3”之间的距离(比前者的3倍要少一些):
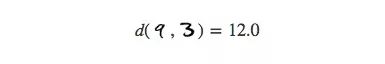
对于相同的数字,它们身上的不同细节变化数不胜数,因此它们的实际平均距离会比我们想象中的高不少。相反地,对于本身距离很远的数字,它们的差异随距离增加,因此遇到两个完全不同的数字也在情理之中。简而言之,在高维空间中,相同数字之间的距离和不同数字之间距离的差距并没有我们想象中的那么大。
基于图像的可视化
因此,如果我们最终希望得到的是低维空间嵌入结果,那优化的目标应该更明确。
我们可以假设存在一个和MNIST距离最接近的图(V,E),它之中的节点就是MNIST里的数据点,并且这些点都连接到原始空间中最接近它的三个点。有了它,我们就能丢掉高维信息,只需思考它嵌入地位空间的方式。
给定这样的图,我们可以使用标准图形布局算法来可视化MNIST。 force-directed graph drawing是一种绘图方法,它的做法是将图的节点定位在二维或三维空间中,使得所有的边或多或少具有相等的长度。在这里,我们可以假设所有数据点都是互相排斥的带电粒子,距离是“弹簧”,这样做之后得到的cost函数就是:
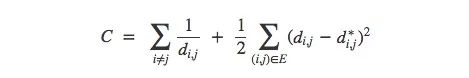

用图像可视化MNIST
上图发现了MNIST中的很多结构,尤其是它似乎找到了不同的MNIST类。虽然它们重叠,但在图像布局优化期间,我们可以发现聚类之间的相互滑动。由于这些连接,最终嵌入低维平面时它们还是保持重叠状态,但我们起码看到了cost函数试图分离它们的尝试。
这也是基于图像的可视化的一个优点。在之前的可视化尝试中,即便我们在某个聚类里看到了某个点,我们也无法确定它是否真的在那儿。但图像可以完全规避这一点,例如如果我们检查着色为红色的数字“0”数据点聚类,我们可以在里面发现一个蓝色点“6”,查看它周围的数据点我们就能知道,这个“6”之所以被归类在这里是因为它写的太差了,长得更像个“0”。
t-SNE
t-SNE是本文介绍的最后一种降维方法,它在深度学习中非常受欢迎,但考虑到其中涉及不少数学知识,所以我们得先理一理。
粗略地说,t-SNE试图优化的东西是保存数据的拓扑结构。对于每一点,它构造了一个概念,即周围的其他点都是它的“邻居”,我们要试图使所有点具有相同数量的“邻居”。因此它的目标就是嵌入并使各个点拥有的“邻居”数相同。
在某些方面,t-SNE很像基于图像的可视化,但它的特色在于将数据点之间的关联性转换为概率,这个点可能是“邻居”,也可能不是“邻居”,每个点成为“邻居”的程度不同。
用t-SNE可视化MNIST
t-SNE通常在揭示数据集聚类和子聚类中有优秀表现,但它容易陷入局部最小值。如下图所示,两侧的红点“0”因为中间的蓝点“6”无法聚集在一起。
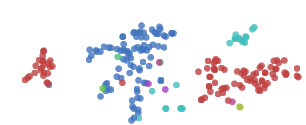
一些技巧可以帮助我们避免这些糟糕的局部极小值。其中首选的方法是增大数据量,考虑到这是一篇演示文章,我们在这里只用了1000个样本,如果用上MNIST全部50000多个数据点,效果会更好。另外就是用模拟退火、调超参等。下图是一个比较好的可视化:
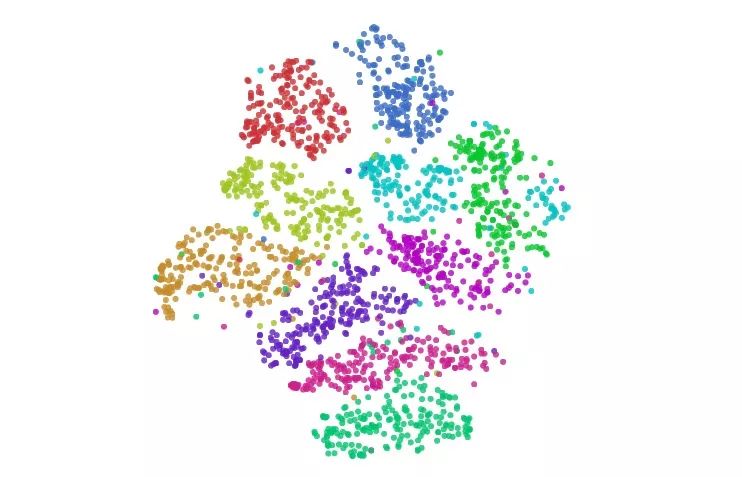
用t-SNE可视化MNIST
在Maaten & Hinton(2008)最初那篇介绍t-SNE的论文里,他们给出了一些更完美的可视化结果,感兴趣的读者可以前往一读。
在我们上面的例子中,t-SNE不仅给出了最好的聚类,我们也可以通过图像从中推测一些东西。

用t-SNE可视化MNIST
图中数字“1”这个聚类被横向水平拉伸,从左向右查看数据点,我们观察到了这个趋势:
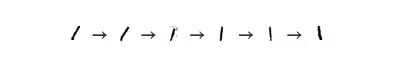
这些“1”先向左倾,再直立,最后向右倾。对此一个靠谱的想法是在MNIST中,相同数字变化的主要因素是倾斜。这很可能是因为MNIST通过多种方式使数字标准化,而这些变化又以直立的手写体为分界线分属两边。这种情况不是孤例,其他数字的分布也或多或少表现出了这个特点。
三维可视化
除了降维到二维平面,三维也是非常常见的一个维度。考虑到之前在平面中许多聚类有重叠,因此我们也可视化了MNIST数字降维到三维的一些情况。

用图像可视化MNIST(3D版)
不出所料,三维版本效果更好。这些聚类分离地很彻底,并且在纠缠时不再重叠。
看到这里我们就能知道为什么分类MNIST数字的准确率达到95%左右很容易,但越往上就越难。在可视化图像中,这些数据的分类十分清晰,因此但凡性能较好的分类器都能达成任务目标。如果要更细化,这就很难了,因为有些手写体确实难以归类。

用MDS可视化MNIST(3D版)
看来MDS的二维比三维表现更好一点。

用t-SNE可视化MNIST
因为t-SNE假想了一大堆邻居,所以各聚类分得更散。但总体而言,它的效果还是不错。
如果你想要将高维数据可视化,那么在三维空间应该比二维更适合。
小结
降维是一个非常发达的领域,本文只抓住了事物表面,还有上百种方法亟待测试,所以各位读者可以亲自动手去试一试。
人们往往很容易陷入一种思维,固执地认定其中一种技术比其他技术更好。但我认为其实大部分方法都是互补的,它们为了做到权衡,都必须放弃一个点来抓住另一个点,如PCA尝试保留线性结构,MDS尝试保留全局几何,而t-SNE尝试保留拓扑(邻域结构)。
这些技术为我们提供了一种获得理解高维数据的方法。尽管直接试图用人的思想来理解高维数据几乎是无望的,但通过这些工具,我们可以开始取得进展。
-
机器视觉与计算机视觉的关系简述2014-05-13 0
-
问一个超简单的计算机逻辑题2014-05-22 0
-
计算机视觉/深度学习领域常用数据集汇总2018-08-29 0
-
CV之YOLO:深度学习之计算机视觉神经网络tiny-yolo-5clessses训练自己的数据集全程记录2018-12-24 0
-
CV之YOLOv3:深度学习之计算机视觉神经网络Yolov3-5clessses训练自己的数据集全程记录2018-12-24 0
-
计算机视觉神经网络资料全集2018-12-24 0
-
自动驾驶系统要完成哪些计算机视觉任务?2020-07-30 0
-
用于计算机视觉训练的图像数据集介绍2021-02-26 0
-
RISC指令集计算机的优点有哪些2021-12-14 0
-
深度学习与传统计算机视觉简介2021-12-23 0
-
计算机视觉贾云德pdf版2017-05-09 1332
-
计算机视觉与机器视觉区别2018-12-08 12076
-
用于计算机视觉训练的图像数据集2022-02-12 1157
-
机器学习和计算机视觉的前20个图像数据集2021-01-28 683
-
机器视觉和计算机视觉的区别2023-02-22 815
全部0条评论

快来发表一下你的评论吧 !

