介绍一种即省时又节约资源的乘除法算法

目前单片机的市场竞争很激烈，许多应用出于性价比的考虑，选择使用程序存储空间较小（如1K，2K）的小资源8位MCU芯片进行开发。一般情况下，这类MCU没有硬件乘法、除法指令，在程序必须使用乘除法运算时，如果单纯依靠编译器调用内部函数库来实现，常常会有代码量偏大、执行效率偏低的缺点。

上海晟矽微电子推出的MC30、MC32系列MCU，采用了RISC架构，在小资源8位MCU领域有广大的用户群和广泛的应用，本文就以晟矽微电的这两个系列产品的指令集为例，结合汇编与C编译平台，给大家介绍一种即省时又节约资源的乘除法算法。

乘法篇

单片机中的乘法是二进制的乘法，也就是把乘数的各个位与被乘数相乘，然后再相加得出，因为乘数和被乘数都是二进制，所以实际编程时每一步的乘法可以用移位实现。

例如：乘数R3=01101101，被乘数R4=11000101，乘积R1R0。步骤如下

1、清空乘积R1R0；

2、乘数的第0位是1，那被乘数R4需要乘上二进制数1，也就是左移0位，加到R1R0里;

3、乘数的第1位是0，忽略；

4、乘数的第2位是1，那被乘数R4需要乘上二进制数100，也就是左移2位，加到R1R0里；

5、乘数的第3位是1，那被乘数R4需要乘上二进制数1000，也就是左移3位，加到R1R0里；

6、乘数的第4位是0，忽略；

7、乘数的第5位是1，那被乘数R4需要乘上二进制数100000，也就是左移5位，加到R1R0里；

8、乘数的第6位是1，那被乘数R4需要乘上二进制数1000000，也就是左移6位，加到R1R0里；

9、乘数的第7位是0，忽略；

10、这时候R1R0里的值就是最后的乘积，至此算法完成。

以上例子运算结果：

R1R0 = R3 * R4= (R4<<6)+(R4<<5)+(R4<<3)+(R4<<2)+R4 = 101001111100001

实际运算流程图见图1.1。

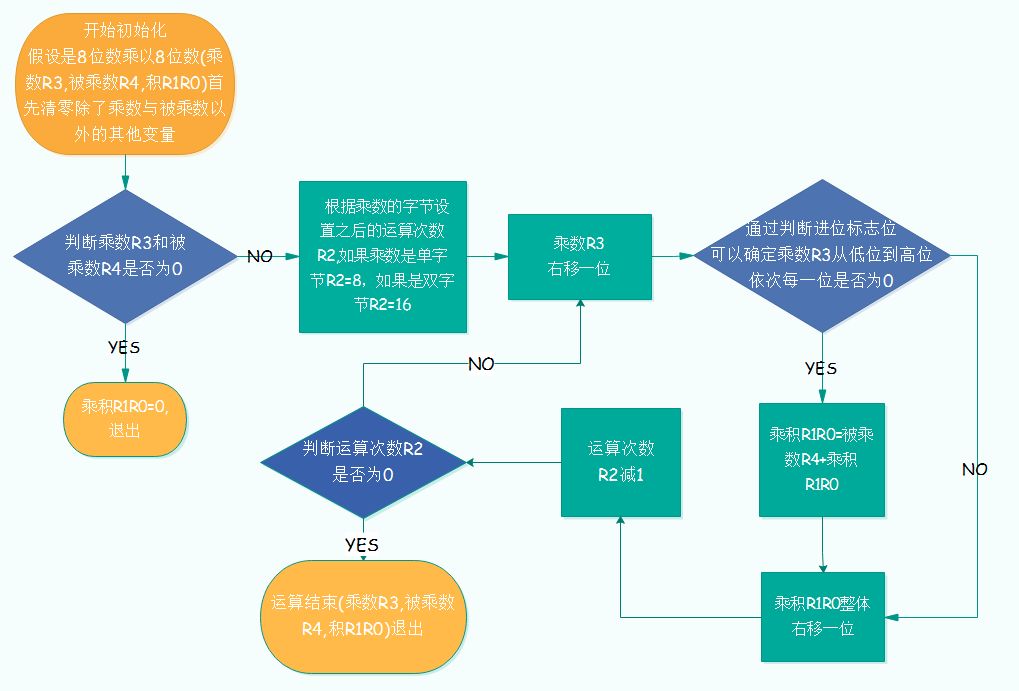
图1.1  汇编乘法运算流程图

在实际的程序设计过程中，程序优化有两个目标，提高程序运行效率，和减少代码量。我们来看下本文提供的汇编算法和普通C语言编程的效率和代码量对比。

表1.1是程序运行效率的对比数据（可能会有小的偏差），很明显汇编编译出来的运行时间要比C语言减少很多。

	汇编（时钟周期）	C语言（时钟周期）
8*8位乘法	79-87	184-190
16*8位乘法	201-210	362-388
16*16位乘法	234-379	396-468

 

表1.1  乘法运算时钟周期对比表

表1.2是程序代码量的对比数据（可能会有小的偏差），汇编占用的程序空间也要比C语言小很多。

	汇编（Byte）	C语言（Byte）
8*8位乘法	15	34
16*8位乘法	19	96
16*16位乘法	31	96

 

表1.2  乘法运算ROM空间使用情况对比表

综上两点，本文介绍的乘法算法各方面使用情况都要比C编译好很多。如果大家在使用过程中，原有的程序不能满足应用需求，例如遇到程序空间不够或者运行时间太久等问题，都可以按照以上方式进行优化。汇编语言最接近机器语言的。在汇编语言中可以直接操作寄存器，调整指令执行顺序。由于汇编语言直接面对硬件平台，而不同的硬件平台的指令集及指令周期均有较大差异，这样会对程序的移植和维护造成一定的不便，所以我们针对精简指令集做了乘法运算的例程，便于大家的移植和理解。

除法篇

单片机中的除法也是二进制的除法，和现实中数学的除法类似，是从被除数的高位开始，按位对除数进行相处取余的运算，得出的余数再和之后的被除数一起再进行新的相除取余的运算，直到除不尽为止，因为单片机中的除法是二进制的，每个步骤除出来的商最大只有1，所以我们实际编程时可以把每一步的除法看作减法运算。

例如：被除数R3R4=1100110001101101，除数R5=11000101，商R1R0，余数R2。步骤如下

1、清空商R1R0，余数R2；

2、被除数放开最高位，第15位，为1，1比除数小，商为0，余数R2为1；

3、上一步余数并上被除数次高位，第14位，得11，11仍然比除数小，商为0，余数R2为11

4、直到放开第8位后，得11001100，比除数大，商得1，余数R2为111；

5、上一步余数并上被除数第7位，得1110，没有除数大，商为0，余数R2为1110；

6、上一步余数并上被除数第6位，得11101，没有除数大，商为0，余数R2为11101；

7、按照以上步骤，直到放开了被除数得第3位，得11101101，比除数大，商为1，余数R2为101000；

8、上一步余数并上被除数第2位，得1010001，没有除数大，商为0，余数R2为1010001；

9、上一步余数并上被除数第1位，得10100010，没有除数大，商为0，余数R2为10100010；

10、上一步余数并上被除数第0位，得101000101，比除数大，商为1，余数R2为10000000；

11、然后把以上所有步骤中得商从左至右依次排列就是最后的商100001001，余数为最后算得的余数10000000。

以上例子运算结果   R1R0 = R3R4 / R5 = 100001001

R2 = R3R4 % R5 = 10000000

实际运算流程图见图2.1。

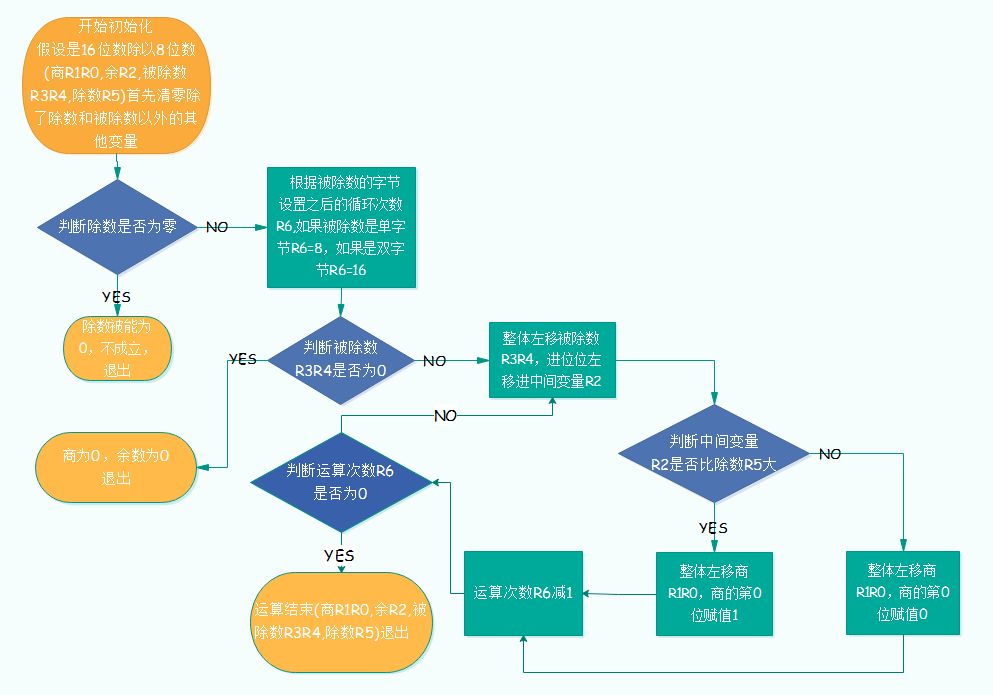
图2.1  汇编除法运算流程图

除法运算的效率，代码量见以下表格

表1.1是程序运行效率和代码量的对比数据（可能会有小的偏差），很明显本文提供的汇编算法要优化的很多。

16/8位除法	汇编	C语言
时钟周期	287-321	740-804
使用空间（Byte）	35	142

 

表2.1  除法运算时钟周期对比表

所以对于除法运算，本文提供的方法也是相对较优的。

以下是针对精简指令集做的除法运算，16/8位的例程，便于大家的移植和理解。