

约束定向增强滤波器技术
描述
本文来自Xiph.org的创始人Christopher Montgomery在Mozilla博客上的分享,他也是Mozilla Daala的贡献者。Christopher Montgomery是多媒体圈的传奇人物,Xiph.org于2000年推出Ogg Vorbis,2013年加入Mozilla,有兴趣的同学可以去Google他的Wiki页面。本文由LiveVideoStack摘译,并由专业的多媒体工程师进行审校。时间仓促,如有错误请在留言中指出。
AV1是由开放媒体联盟(AOM)开发的新一代通用视频编解码器。该联盟是使用谷歌的VPx编解码器,思科的Thor编解码器和Mozilla的Xiph.Org的Daala编解码器作为起点来开发新的编解码器。AV1的性能超越了VP9和HEVC,使得其成为下一代编解码器。AV1编解码器拥有开源FOSS许可证,并且永远是免版税的。
作为探索AV1及首次应用于产品化编码器系列文章的第二篇。系列的第一篇则发表于Xiph.org网站,研究了从亮度特征预测色度的技术。今天,我们将介绍约束定向增强滤波器技术。如果你一直想知道为什么要编写一个编解码器,那么请正襟危坐,仔细阅读!
AV1中的滤波操作
实际上,所有的视频编解码器都使用增强滤波器来改善主观输出质量。
“增强滤波器”是指不需要编码图像信息或提高客观编码效率,而是使输出在某种程度上看起来更好的技术。增强滤波器的使用必须非常小心,因为它们往往会丢失一部分信息。因此它们偶尔会被视为欺骗性作弊,以使得输出质量看起来比实际更好。
但这是不公平的。增强滤波器旨在减轻或消除客观指标盲目的,但对人眼来说是显而易见的特定伪像。因此,即使滤波是作弊的一种形式,一个好的视频编解码器也需要它可以利用所有的实用有效的作弊手段。
滤波器可分为多个类别。首先,滤波器可以是规范的或非规范的。规范滤波器是编解码器的必要部分;如果没有它,就无法正确地解码视频。而非规范滤波器则为可选项。
其次,可根据滤波器的应用位置进行划分。如:在编码开始之前就应用于输入的预处理滤波器,在解码完成之后应用于输出的后处理滤波器,以及在编码循环中作为编码处理的集成部分的环路滤波器。预处理和后处理滤波器通常是非规范的,位于编解码器之外。根据定义来看,环路滤波器应该是规范的,它也是编解码器本身的一部分;它们用于编码优化过程,并应用于存储的参考帧或帧间编码。
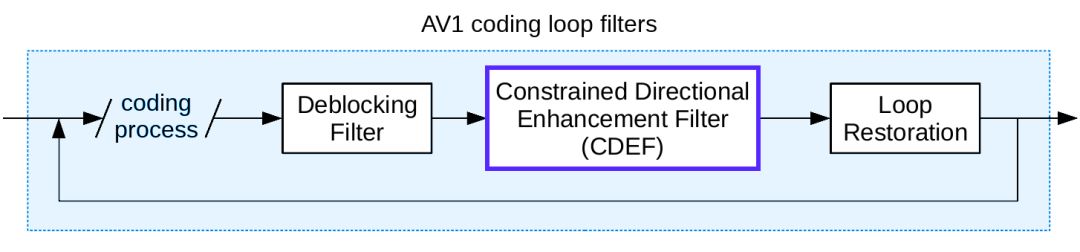
AV1在编码循环中使用了三个标准增强滤波器。第一个是去块效应滤波器,它的功能就是其字面意思:消除编码块边缘明显的边界伪影。尽管DCT相对非常适合于压缩自然图像中的相邻像素的空间冗余,但它往往将误差集中在块边缘处。请记住,消除这种块效应倾向是Daala使用重叠变换的主要原因,但AV1是一种具有硬块边缘的更传统的编解码器。因此,它需要一个传统的去块效应滤波器来平滑块边缘的块斑现象。
传统的基于DCT块的编解码器中块效应示例。块边缘的误差因形成硬边缘而特别明显。更糟糕的是,DCT(以及DCT系列中的其他变换)倾向于将误差集中在块边缘,从而使得问题变得更为复杂。
三个过滤器中的最后一个是环路恢复滤波器。它是由两个可配置与可开关的滤波器,Wiener滤波器和Self-Guided滤波器组成。两者均是卷积滤波器,通过构建卷积核以恢复原始输入图像的某些质量损失,并且通常用于去噪和/或边缘增强。对AV1来说,它们是有效的通用去噪滤波器,通过可配置的模糊量来消除DCT 基础噪声。
这里,位于二者之间的过滤器,即约束定向增强滤波器(CDEF)是我们感兴趣的并将重点介绍的滤波器;与环路恢复滤波器相同的是,它可以消除尖锐边缘周围的振铃和基础噪声;但与环路恢复滤波器不同的是,它具有方向性。它可以顺着边缘,而不是像大多数滤波器那样在所有方向上盲目滤波,这使得CDEF特别神奇;它也是视频编码中应用的第一个可实现且有用的方向滤波器。
CDEF漫长而曲折的道路
CDEF的故事并不是一帆风顺的;它是漫长的,充满了回溯、离题和死胡同。
CDEF将多个研究路径结合在一起,每个路径都为AV1中最终定稿的约束定向增强滤波器提供了一个想法或灵感。CDEF的“方向性”方面在实施中特别新颖,却是从几个不同的地方汲取了想法和灵感。
使用DCT变换或类DCT变换是要使用更少的数字来表示该像素块。DCT非常擅长压缩大多数视觉图像中的能量,也就是说,它倾向于将分散的像素图案集中至几个重要的输出系数中。
但DCT的压缩效率也有例外。举两个最常见的例子,DCT并不能很好地表示方向边缘或模式。如果我们绘制陡峭的斜边缘的DCT输出,会发现输出系数也形成陡峭的斜边!转换后的边缘是不同的,但它仍然存在,并且通常比它转换前的更复杂—即压缩失败了!

如果有的话,锐利特征是基于DCT的编解码器的传统问题,因为它们不能很好地压缩。在这里,我们看到一个尖锐的边缘(左)及其DCT变换系数(右)。原始边缘的能量以定向波纹图案通过DCT输出来传播。
在过去的二十年中,视频编解码器研究越来越多地关注本质上带有方向性的变换,滤波和预测方法,以便更好地表示方向性的边缘和模式,并纠正DCT的这一基本限制。
经典定向预测器
定向帧内预测是现代视频编解码器中使用的最著名的定向技术之一。我们都熟悉H.264和VP9的方向性预测模式,编解码器会基于已解码块周围的像素来预测方向模式。目的是在变换之前去除(或大大减少)方向性边缘中包含的能量。通过预测或去除无法压缩的特征,我们可以提高编解码器的整体效率。
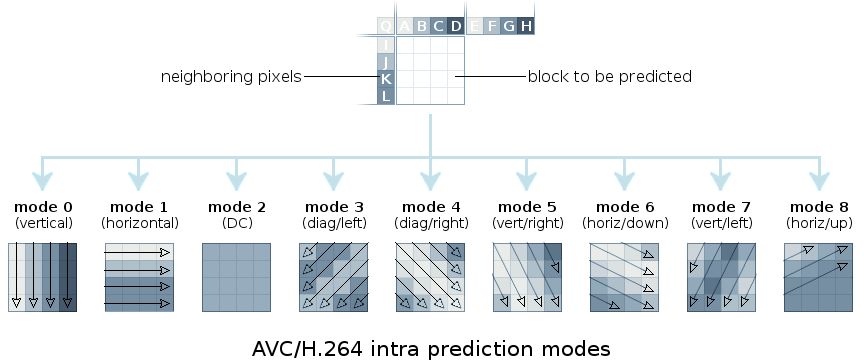
AVC / H.264中, 4×4块可使用的9种预测模式图示:8种方向性预测,加简单的DC预测。
运动补偿,也可以算作一种方向预测。它是在特定方向上移动块,也是在DCT之前预测消除冗余。块的匹配是指向性的并在滤波之后完成。和帧内方向预测一样,当匹配位置不是整像素时,会用到插值滤波器。
定向滤波器
如前面所提到的,视频编解码器大量使用滤波操作来消除块效应和基底噪声。尽管滤波器是用于二维平面,但滤波器本身往往可分解为水平滤波和垂直滤波两步。
定向滤波技术尝试在非水平或垂直的方向上进行滤波。该技术在图像处理中已经很常见,其中噪声消除和特殊效果滤波器通常是边缘和方向感知的。然而,这些定向滤波器通常是基于对定向变换的输出进行滤波。例如,我之前基于双树复数小波变换编写的图像去噪滤波器。
在视频编码领域我们最感兴趣的定向滤波器是沿着一个方向来直接处理像素的,而不是对定向变换的频域输出结果进行滤波操作。如果你尝试设计这样一个怪异的滤波器,你很快就会遇到第一个关键的设计问题:当你的滤波器抽头位置不再横平竖直地坐落在网格排列的像素上时,你如何“沿”水平和垂直以外的方向呢?
一种可能是在高质量图像处理中使用的经典方法:变换滤波器的内核并根据需要对像素空间重新采样。有人甚至认为这是唯一的“正确”或“完善”的答案。这个方法用于亚像素运动补偿和经常使用快速逼近的定向预测,但在没有适当的重采样的情况下往往无法取得很好的结果。
也就是说,即使是快速逼近法其代价也很高,因为你原本并不需要这么做。因此如果可能的话,尽量避免重新采样步骤是值得的。速度方面的代价是视频编码中很少使用定向滤波的原因之一。
定向变换
定向变换试图在其自身变换过程中解决DCT变换的边缘压缩问题。
实验性的定向变换分为两类。使用固有方向基的变换,例如定向小波。这类变换往往是过采样/过完备,也就是说,它们产生的输出数据多于输入数据—而且通常是多很多。这看起来可能像是违背了初衷:原本你是想减少数据量,而不是增加!但是这些变换仍然能够聚集能量,并且编码器仍然选择一些小的输出子集进行编码,因此它与普通的有损DCT编码没有什么不同。也就是说,过度完备的变换在内存和计算方面往往代价高昂。因此,它们并未在主流视频编码中占据一席之地。
第二类定向变换采用常规的非定向变换,如DCT,并通过改变输入或输出来修改它。改变可以是重采样的形式,矩阵乘法(可以被视为重采样的特殊形式)或者是改变输入数据顺序的技巧。
显然,第二种变换是性能最强的,因为速度很快。重新排列数字并不需要数学运算。
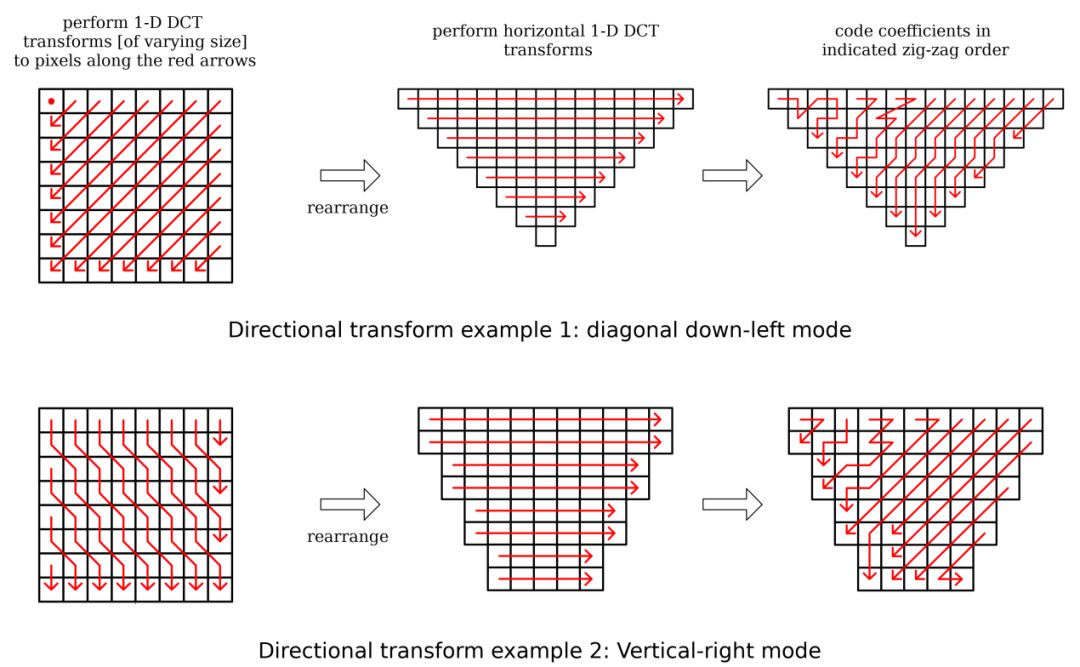
使用像素和系数重新排列而非重采样滤波器在不同方向上实现定向变换的两个示例。
示例来自于论文An Overview of Directional Transforms in Image Coding,
(http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.187.640&rep=rep1&type=pdf) by Xu, Zeng, and Wu。
一些实际的复杂性使得实现变得棘手。重排列以使对角线边缘[大多数]成为垂直或水平线,使得输入变为非方形矩阵。从概念上讲,这不是问题;二维DCT变换是可分解的,而且因为我们可以独立地运行行和列变换,所以我们可以简单地为每个长度的行和列使用不同大小的一维DCT变换,如上图所示。实际上,这意味着我们需要针对每种可能的列长度进行不同的DCT分解,这使得硬件团队在实现时非常头疼。
还有其他方法可以处理重新排列的非方形区域,或者提出重新采样方案,以保持输入方形或仅对输出进行操作。下面提到的大多数定向变换论文讨论了各种解决方案。
但是现在,定向变换的故事大多结束了。一旦你解决了方向变换的各种复杂问题并部署了一些实用的东西,出乎意料的原因使得它们在现代编解码器中并不能应用—即定向变换技术与变块尺寸技术竞争获得收益。也就是说,在具有固定的块大小的编解码器中,单独添加定向变换技术可以获得不错的性能提升。而单独添加可变块尺寸大小技术则可以获得更好的收益。但联合使用可变块尺寸技术和定向变换技术相对单独采用可变块大小技术却没有任何收益。可变块大小技术已经有效地消除了方向变换所利用的同类冗余,至少是我们目前知道的并且已经处理地很成熟的那些冗余。
在Daala研究期间,Nathan Egge和我都进行了广泛的定向变换实验。我从输入和输出端考虑问题,使用稀疏矩阵乘法将对角线边缘的输出转换为垂直/水平排列。Nathan通过重新排列的输入对主流定向方法进行了测试。我们得出了相同的结论:额外的复杂度并没有带来客观或主观的收益。
Daala(以及其他编解码器)中的定向变换可能是失败的,但这一研究恰好回答了之前提出的问题:如何在没有高昂代价的重采样步骤的情况下快速沿边缘滤波?答案是:不重新采样。通过沿最近的整像素移动来估算角度。通过字面或概念上重新排列像素来估算转换后的内核。这种方法会引入一些混叠,但它很有效,而且速度足够快。
定向预测器,第2部分:Daala编年史
Daala方面关于CDEF的工作则是尝试做一些完全不同的事情:常规的,枯燥的,定向的帧内预测。或者至少在Daala编解码器中变成了常规。
在刚刚开始研究的时候,我写了Daala的频域帧内预测方案。这个方案背后的数学是有效的,对此没有任何的担忧。然而,一个简单的实现需要巨大的矩阵乘法,这对于产品化的编解码器来说太昂贵了。我们希望稀疏化——消除对预测没有太大贡献的矩阵元素——这样就可以将计算代价降低到完整乘法的百分之几。
稀疏化并未如预期的那样发挥作用。至少在我们实现的过程中,为使技术变得切实可行,稀疏化丢失了太多的信息。
当然,Daala仍然需要某种形式的帧内预测,Jean-Marc Valin想到了一个方法:一个独立的在空间域工作的预测编解码器,然后再映射到频域Daala编解码器上。作为一种与Daala编解码器协同工作但不依赖于Daala编解码器的共生体,它不受Daala的搭接和频域要求的限制。这就是Intra Paint。
应用于照片Sydney Harbor的Intra Paint预测算法的示例。视觉输出方向明确,并且很好地遵循原始图像中的边缘和特征,边缘清晰的同时产生令人愉悦(可能有些奇怪)的结果。
Intra paint的工作方式也很新颖;它仅沿着块的边缘编码一维向量,然后沿所选方向扫描图案。这就像喷出一系列彩色油漆点,然后在开放区域向不同方向大范围延伸油漆。
Intra paint很有前景,并且自身会产生了一些非常漂亮的结果,但因效率不足以作为标准的内部预测器。它根本没有获得足够的比特位来编码它自己的信息。
原始悉尼港照片与Intra Paint结果之间的残差。尽管Intra Paint的视觉效果令人满意,但我们发现它不是一个客观上准确的预测器。原始照片和Intra Paint结果之间的差异相当大,即使是沿着它看起来重现良好的许多边缘也是如此。
Intra paint的“失败”再次播下了不同想法的种子;尽管Intra paint对于预测器来说可能不够客观精确,但其大部分输出主观上看起来都很好。也许paint技术可以用作后处理滤波器器来改善主观视觉质量?Intra paint很好地遵循尖锐边缘,因此可能用于消除沿最强边缘趋于最强的基础噪声。这是Daala原始paint-deringing滤波器背后的思路,最终演化为CDEF。
关于方向预测的主题还有一个有趣的提及,尽管它目前也是视频编码的死胡同。David Schleef实现了一个有趣的边缘/方向感知重采样滤波器,称为边缘定向插值(EDI)。其他编解码器(例如VPx系列和AV1)已经尝试了下采样参考帧,传送下采样的参考帧以节省编码比特,然后对参考帧进行上采样以便以全分辨率使用。我们希望EDI提供的改进的上采样/插值可以将该技术提高到可用的程度。我们还希望使用EDI作为运动补偿中改进的亚像素插值滤波器。遗憾的是,这些想法均尚未实现。
缩小差距,合并思路
在这一点上,我已经描述了完成CDEF所需的所有主要背景,但按时间顺序,这个故事涉及到更多长期的摸索。Intra paint产生了原始的Daala paint-dering滤波器,其重新实现了intra-paint算法以执行作为后滤波器的去除操作。事实证明,Paint-dering在生产中使用速度太慢了。
结果是,我们整理了从Intra paint学到的经验教训,最后放弃了实验。Daala引入了Thor的CLPF一段时间,然后Jean-Marc基于Intra paint边缘方向搜索(速度快且效果很好)和条件替换滤波器(CRF)构建了第二个更快的Daala去振铃滤波器。CRF在某种程度上受到中值滤波器的启发,产生类似于双边滤波器的结果,但本质上是高度可矢量化的,因此速度更快。
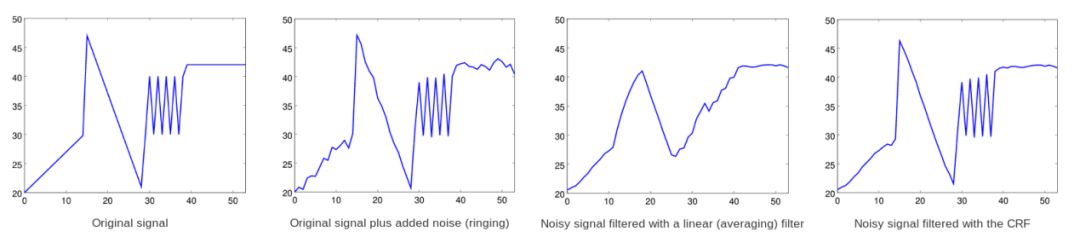
7抽头线性滤波器vs受约束的替换滤波器的演示,应用于有噪声的一维信号,其中噪声旨在模拟量化对原始信号的影响。
最终的Daala去振铃滤波器使用了两个一维CRF滤波器,一个沿边缘方向运行的7抽头滤波器,以及一个较弱的5抽头滤波器。两个滤波器仅对整像素进行操作,不执行重采样。那时,Daala 的去振铃过滤器看起来很像我们现在所知的CDEF。
最近我们将Daala作为输入编解码器提交给AOM,这个中间滤波器促成了AV1 daala_dering实验。思科也提交了自己的去振铃滤波器,即Thor编解码器中的约束低通滤波器(CLPF)。 有一段时间,两个去振铃滤波器共存于AV1实验代码库中,它们可以单独启用,甚至可以一起运行。这使得在操作中能注意到在它们的操作中有效的协同作用,以及在滤波器各个阶段中的其他相似之处。
因此,我们最终获得了CDEF:将Cisco的CLPF滤波器和第二版本的Daala去振铃滤波器合并为一个高性能,方向感知的去振铃滤波器。
现代CDEF
CDEF滤波器很简单,与我们之前的滤波器非常相似。它由我们之前使用过的三个部分(定向搜索,约束替换/低通滤波器和整像素抽头放置)构成。考虑到这一点冗长的背景序言,你几乎可以看看完成的CDEF并思考,“是吗?其余部分在哪里?”CDEF是通过使滤波器的细节完全正确而不是仅仅使其变得越来越复杂而获得的增益的示例。简单有效才是目的。
方向搜索
CDEF在特定方向上运行,因此有必要确定该方向。使用的搜索算法与intra paint和paint-dering相同,并且有八个可能的方向。
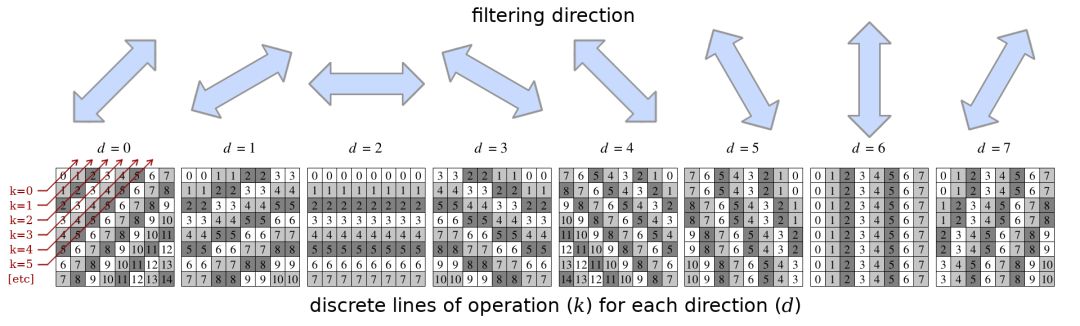
当前CDEF滤波器的八个可能的滤波方向。每个方向块中的编号行对应于方向搜索中的参数“k”。
我们通过计算输入块的“方向”变量来确定滤波器方向,每个方向一个数值,沿着所选方向的线上的所有像素被强制转换为相同的值。然后我们选择结果与原始块最匹配的方向。方法是,对于每个方向d,我们首先找到每条线k中的像素的平均值,然后沿每条线求给定像素值与该线上像素的平均值之间的平方差的和。
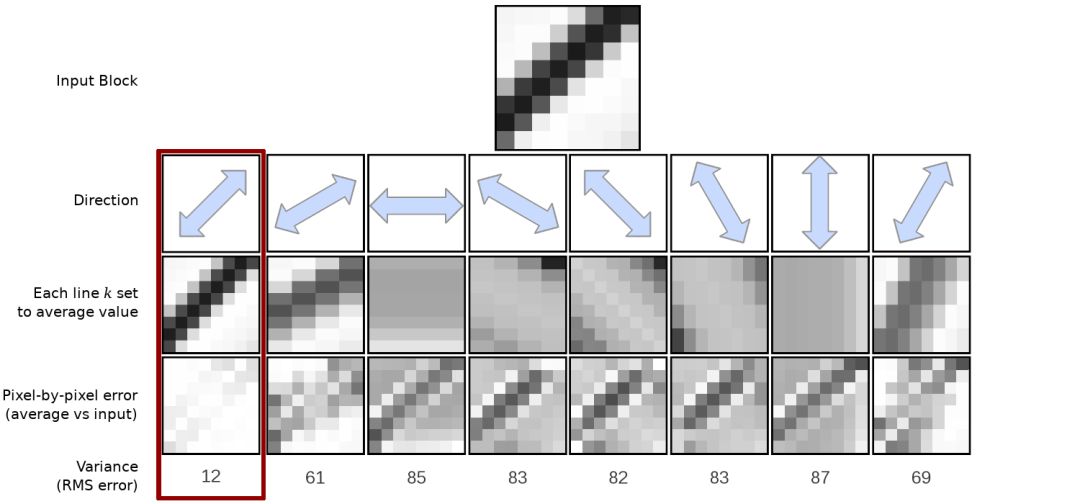
选择与输入块最佳匹配的方向d的示例过程。首先,我们确定每个方向的每个操作线k的平均像素值。如上图所示,每条线k的每个像素设置为该平均值。然后,逐像素按平均预测值减去输入值,再对残差求和。选择具有最低误差/方差的方向作为最佳方向。
这给出了总平方误差,最小总平方误差即是我们选择的方向。虽然上面的图例也是如此,但没有理由将平方误差转换为方差;每个方向都考虑相同的像素数,因此两者都会选择相同的答案。这就节省额外的除法操作!
这是计算方向误差直观,长期的方法。 我们可以将此机械过程简化为以下等式:
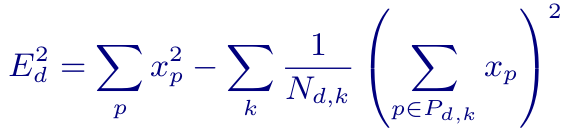
在该等式中,E是误差,p是像素,x_p是像素的值,k是上面方向图中的编号行之一,N_(d,k)是方向d的编号行k的基数(像素数)。 这个等式在实践中可以简化; 例如,对于每个给定的d,第一项是相同的。最后,CDEF的AV1实现目前需要每像素5.875个加法和1.9375次乘法,并且可以进行深度矢量化,使得计算量小于8×8 DCT变换操作。
滤波器抽头
CDEF滤波器在整个块上逐个像素地工作。方向d选择要使用的特定方向滤波器,每个滤波器由一组滤波器抽头(即输入像素位置)和抽头权重组成。
CDEF从概念上构建了由两个一维滤波器组成的方向滤波器。主滤波器沿选定的方向运行,就像Daala去环过滤器一样。二级滤波器以交叉模式运行两次,与主滤波器成45°角,就像Thor的CLPF一样。
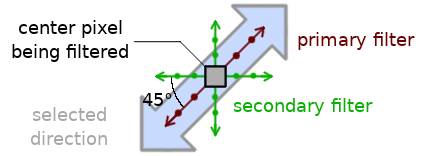
相对于所选方向d的主要和次要一维滤波器方向性的图示。主滤波器沿选定的滤波器方向运行,二级滤波器以45°角穿过所选方向。块中的每个像素都被相同地滤波。
滤波器以通常在像素之间放置理想抽头位置的角度运行。我们选择最接近的精确像素位置,注意构建对称滤波器内核,而不是重新采样。
滤波器中的每个抽头也具有固定权重。滤波过程采用每个抽头的输入值,应用约束函数,将结果乘以抽头的固定权重,然后将此输出值加至被滤波的像素。
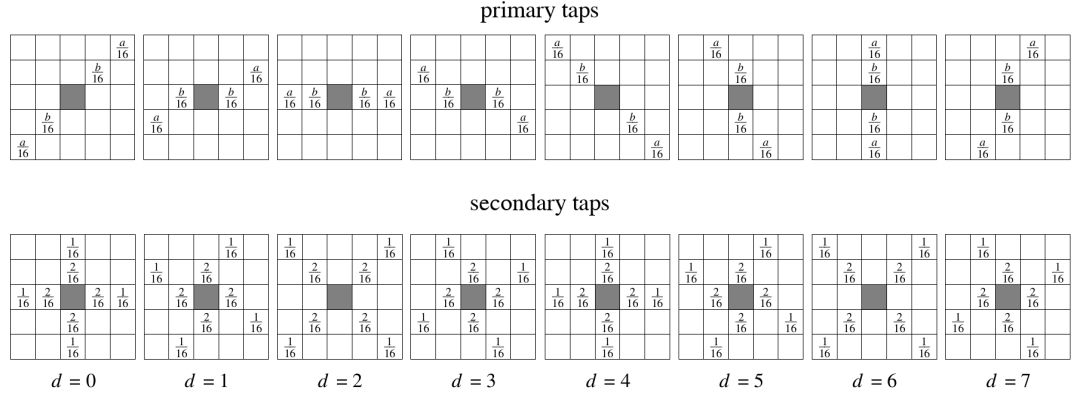
主要的和次要的抽头位置以及滤波器方向的固定权重(w)。对于主要抽头,偶数强度a = 2,b = 4,而对于奇数强度a = 3,b = 3。过滤后的像素以灰色显示。
实践中,主滤波器和二级滤波器并不是单独运行的,而是组合成一步运行的单个滤波器内核。
约束函数
CDEF使用约束低通滤波器,其中每个滤波器抽头的值首先用约束函数来处理(公式见下),参数如下:抽头系数和被滤波的像素的残差d,滤波器强度S和滤波器阻尼参数D:
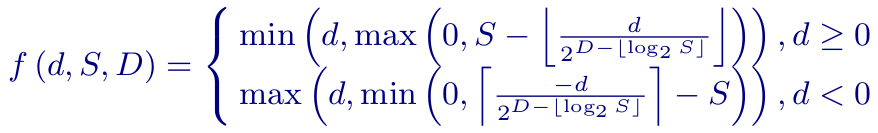
约束函数会弱化或者完全排除那些与被滤波像素差异过大的像素。若抽头系数与中心像素值(由强度参数S定义)的差值落在某一范围,则被完整考虑;若差值落在强度和阻尼参数之间,则被约束。最终,超出阻尼参数的抽头系数差值被忽略了。
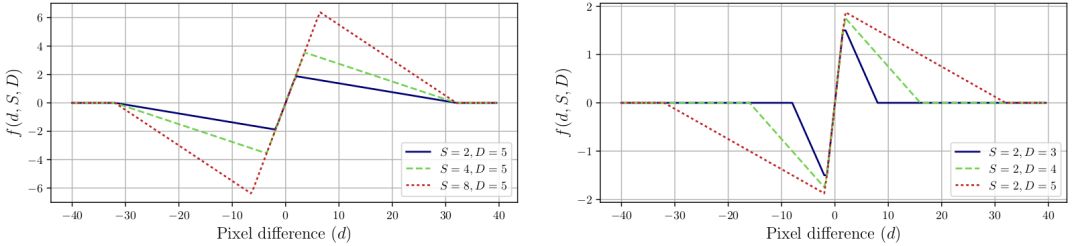
约束函数的图示。在两个图中,x轴表示中心像素和抽头像素之间的差值(d),y轴表示约束函数的输出值。左图显示了改变强度(S)的效果。右图显示了改变阻尼(D)的效果。
然后将约束函数的输出值乘以与相对于中心像素的每个抽头位置相关联的固定权重。最后,将得到的值(每个抽头对应一个值)加到中心滤波像素,得到最终的滤波像素值。总结为:
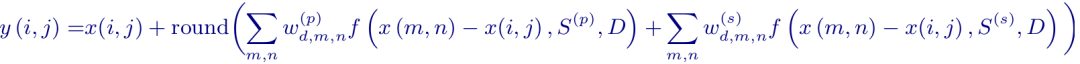
引入的(p)和(s)参数分别表示主要和次要抽头组的值。
还有一些不难理解的实现细节,如四舍五入与修剪函数,都可以在完整的CDEF文件中找到。
结果
CDEF旨在图像的硬边缘附近消除或减少基础噪声和振铃效应,同时也不模糊或损坏该边缘。正如现在AV1中所使用的,效果细微但一致。将来有可能会更加依赖于CDEF。
图像Fruits的编码中减少振铃/基础噪声的例子。第一个插图特写显示未经CDEF处理的区域,第二个插图显示经CDEF处理后的相同区域。
增强滤波器的数值必须通过主观测试来确定。更好的客观指标数字产生的效果也不一定令人震惊,但是推动CDEF的视觉改进大多是在原始客观测试工具(如PSNR或SSIM)的评估能力之外。
因此,我们进行了多轮主观测试。首先是在CDEF的开发过程中(当时Daala dering和Thor CLPF仍然是技术竞争对手),然后对合并的CDEF滤波器进行更广泛的测试。由于CDEF是前几代编解码器中从未出现过的新的滤波器,因此测试主要包括启用了CDEF的AV1和不启用CDEF的AV1。
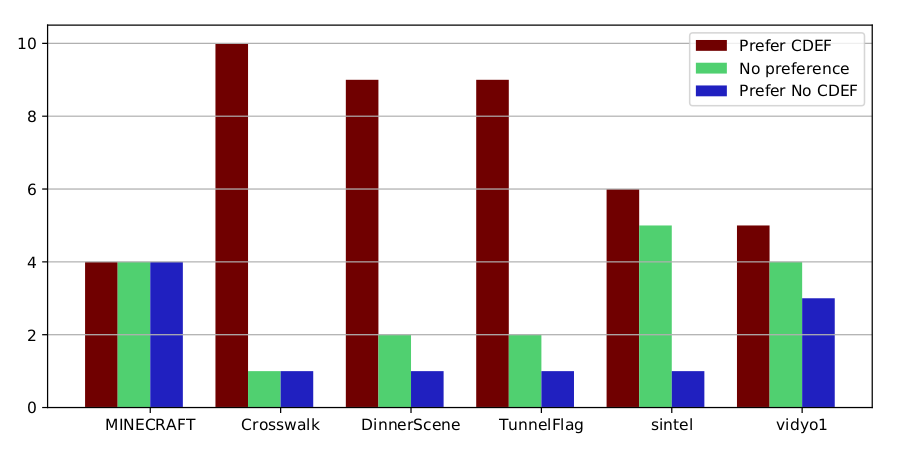
对于高延迟配置,CDEF与no CDEF的主观A-B比较结果。
主观结果显示,6个截断中有3个具有统计学意义(p <.05)。这通常对应于编码效率5-10%的提升,对于添加到其他成熟编解码器的单个工具而言,这是一个相当大的获益。
正如预期的那样,客观测试显示了约1%的适度改进,但客观测试仅在与主观结果一致的情况下才有用。主观测试是金牌标准,且主观结果清晰明了。
测试还表明,在使用较少的编解码器“工具”进行编码时,CDEF的性能会更好;与定向变换一样,CDEF正在与AV1中其他更复杂的技术竞争来获得编码收益。由于CDEF简单,小巧,快速,因此可以提供未来降低AV1编码器复杂度的方法。就解码器复杂度而言,CDEF体现了AV1解码器复杂度的3%~10%,具体将取决于该编解码的配置。
-
基于AccelDSP的自适应滤波器设计2010-04-24 0
-
转:有源滤波器和无源滤波器2011-07-28 0
-
低通滤波器如何设计?2011-11-07 0
-
LTCC滤波器2016-11-15 0
-
传导噪声分析技术是滤波器设计的基础2019-06-20 0
-
滤波和滤波器2019-06-28 0
-
滤波器技术的发展现状2019-07-29 0
-
如何设计高频增强电路与低通滤波器电路?2021-02-25 0
-
请问滤波器技术是什么?2021-04-20 0
-
高通滤波器、低通滤波器、带通滤波器、带阻滤波器、检波器和选频2022-08-25 0
-
光滤波器,什么是光滤波器2010-04-02 2218
-
滤波器的技术指标2010-04-13 7734
-
什么是SAW滤波器技术,它的原理及技术特点是什么2020-01-30 31838
-
IIR滤波器和FIR滤波器的区别2023-06-03 15357
-
增强型IEC插座电源滤波器介绍2023-11-08 462
全部0条评论

快来发表一下你的评论吧 !

