比特币51%攻击是什么？比特币6个确认数是怎么得到的？

一、51%攻击

51%攻击指的是，有人掌握了全网一半以上的算力，就可以和全网其他算力进行对抗，更改区块链记录了。最根本的原因是比特币区块链采取的是最长链原则，即当前最长的链被认为是主链，是正确的链。51%具体能做什么呢？

1. 假设51%算力仍然是遵循比特币的规则

这个时候，仍然需要签名才能进行转账交易等，那么51%攻击，不能修改别人的账户下的金额，不能将别人账户金额转到自己的账户下，只能对自己的账户进行操作，比如双重支付(双重支付可以有两种方式：要么是在交易被确认之前，要么攻击者通过块链分叉来完成)、阻止确认其他交易。

2. 假设51%算力不遵循比特币的规则

这个时候，51%算力可以修改区块链规则，比如，放弃非对称加密的签名机制，转账不需要签名也可以进行，51%算力就可以将其他账户下的金额转到自己名下，因为他掌握了一半以上的算力，所有规则都可以修改，不需要其他算力的参与(因为长远来看，他总是能跑赢其他算力)。

二、6个确认数

为啥掌握51%的算力就能破坏比特币网络呢？从直观感觉上确实如此，将攻击节点算力和诚实节点算力当作两个人，挖矿行为就像赛跑一样，当然是速度快的人最终赢得比赛。其实中本聪在论文中做了数学上的分析。另外，现在比特币转账，都建议等待6个确认数之后，资金才认为是安全的，在他的论文中也做了解释。

首先，所有推导都有一个前提，就是区块随着时间按照大致恒定的速度产生，也就是说，每间隔T0(10分钟)产生且只产生一个区块。

假设当前网络算力是H，诚实节点算力是pH，攻击节点算力是qH，p + q = 1。因为算力本身就是指每个固定时间间隔内能计算Hash的次数，在比特币中，每10分钟产生一个区块，我们可以将10分钟当做一个最小的时间间隔，那么诚实节点算力和攻击节点算力是说：每10分钟发起一次计算的比赛，在这10分钟内，诚实节点能计算k * p次，攻击节点能计算k * q次(k只是一个系数而已，并不重要，重要的是比值)，由前提可知：平均意义上，不存在诚实节点和攻击节点都没挖出区块(某个10分钟存在这个情况的话，那么下一个10分钟会降低挖矿难度)，也不存在诚实节点和攻击节点都挖出区块(某个10分钟存在这个情况的话，那么下一个10分钟会增加挖矿难度)。所以可以这样认为：诚实节点有概率p挖出一个区块(此时，攻击节点没有挖出区块)，攻击节点有概率q挖出一个区块(此时，诚实节点没有挖出区块)！即使诚实节点和攻击节点在两条分叉链上互不影响的挖矿，整个区块链网络也符合这个速度上的特点，这点是理解后面公式的关键。

关于某个交易得到多少个确认数之后资金才是安全的这个问题，在中本聪的论文中，将这个问题，分为两步(假设是n个确认数之后)：

1) n是指，在该交易之后，诚实节点已经挖出了n块，也就是诚实节点对这个交易做了n次确认，因为攻击节点的目的是破坏这个交易，不会浪费自己丁点儿的算力对这个交易做任何确认。这个时候，攻击节点挖出了多少块？(可以理解为，该交易之后，攻击节点就在暗地里将区块链条分叉了，并且不将自己分叉之后的工作放到区块上，而是一直在自己的链条上单独挖矿，等到合适的时机，才会公开自己的工作)

2) 假设这个时候，攻击节点挖出了m块，和诚实节点差距是z = n – m，攻击节点弥补这个差距，追上诚实节点的可能性是多大？

先看第一个问题，中本聪从固定时间间隔的角度出发，他认为，诚实节点T0内挖出一个区块的概率是p，那么平均而言，T0 / p 的时间间隔肯定能挖出一个区块，那么诚实节点挖出n块，共消耗了To * n / p的时间间隔。攻击节点T0内挖出一个区块的概率是q，那么T0 * n / p的时间间隔内，平均而言肯定能挖出q * n / p块，而且每个T0 * n / p的时间间隔内，挖出的块数差不多。将T0 * n / p当做一个单位时间间隔，那么求解的问题是：单位时间内随机事件发生的次数的概率分布。而泊松分布就是描述这个概率的工具。可以参见：维基百科-泊松分布 。λ 表示单位时间间隔内发生的次数，即为q * n / p。

而 Analysis of hashrate-based double-spending 这篇论文认为，不应该从固定时间间隔的角度进行估算，认为中本聪的计算只是一个简化模型。该论文认为，依然从块数出发，相当于：攻击节点在经历至少n次失败(诚实节点挖出了n块)，能挖出的块数，而负二项分布就是描述这个问题的工具，可以参见：维基百科-负二项分布。这个概率公式很简单，不做解释，可以参见论文。该论文最后得出的概率值，和中本聪的模型的概率值大致相当，只是略有差别。

接着看第二个问题，这里再次说一下推导的前提，就是区块随着时间按照大致恒定的速度产生，也就是说，每间隔T0(10分钟)产生且只产生一个区块。明确了这个前提，就能发现，其实诚实节点和攻击节点是互斥的，每10分钟只能有其中之一节点发现一个区块，即使他们可能在两个分叉上。那么这个问题就像中本聪在论文中说的，可以等同于赌徒破产问题，可以参见：维基百科-赌徒破产问题 或者 赌徒破产问题。其中的递推公式

Pa = pPa+1 + q Pa-1,　　a=1,2,…,N-1

是说，假设初始有a个，如果以概率p获得一个金币，那么就等同于初始有a + 1个金币，如果以概率q失去一个金币，那么就等同于初始只有a – 1个金币。应用到比特币中，可以从诚实节点的角度出发，理解为，初始的时候，诚实节点有z个金币，怎么赌博而失去了所有z个金币或者财富一直增加。具体请参照中本聪的论文。

下面是Analysis of hashrate-based double-spending 中列出的，不同攻击节点q概率和等待确认数n的情况下，攻击节点追赶上的概率(因为该论文提出的模型和中本聪提出的模型计算结果相差不大，并且提供的数据比较全，所以使用这个表格)

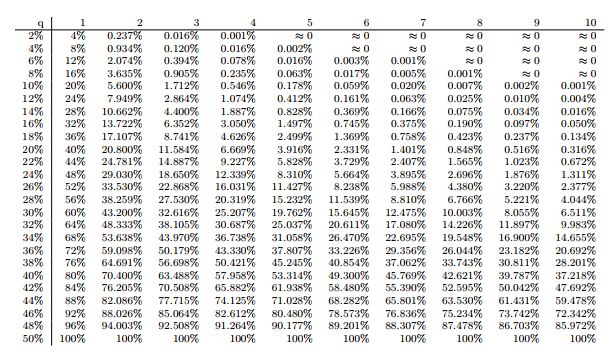
6个确认数是怎么得到的呢？是假设攻击节点算力在10%左右，发起攻击成功概率小于0.1%的确认数，从上表中可以看出是6。