高斯随机噪声实时生成实现方法研究

摘要：提出了一种面向硬件的均值、方差的高斯随机噪声生成方法。改进了传统的采用蒙特卡洛方法实现均匀分布噪声到同分布噪声的快速转化，利用映射函数方法实现个转为，最大随度地降低运算量。实验证明本方法具有快速、高精度等优点.

高斯随机噪声在信号分析和处理中具有重要的价值。本文具体讨论了一种面向硬件的高斯噪声快速生成算法。算法原理为通过映射表法将均匀噪声转化生成高斯随机噪声。本方法占有内存小、运算速度快、精度高。实验证明该方法能够为视频图像实时添加高斯噪声。

图1

    原理框图如图1所示。图1左半部分为均匀噪声生成部分，采用模数取余法，依靠已有的K个随机数种子，不断生成新的随机数，并将之向外输出。图1右半部分采用左半部分的输出值生成映射表地址，将查表后得到的结果输出，即为所要求的高斯噪声值结果。

1 生成均匀分布噪声

设x(1)，…，x(k)是给定的k个随机数，在(-X，X)内均匀分布，相互独立。第k+1个随机数由x(1)和x(k)按照模X相加得到：

即x(k+1)仍然是(-X，X)之间的随机数。在下一次运算时，将x(k+1)移到x(k)的位置，xk)移到x(k-1)，……，x(2)移到x{1}，然后再做模X运算，相加得到x(k+2)，如此循环，产生序列{xn}。

首先讨论上面的模X运算。对于采用补码运算的处理器而言，只要取X为处理器字长，则在不考虑进位的情况下，通常的加法就是模加运算。

然后采用数据结构实现上面的循环机制。设两个指针：头指针head和尾指针tail。每计算完一次噪声值后，两个指针都要向下移动一个位置。已到序列尾部，则重新指到序列的头部，即按照加1模K运算：

    为了计算方便，选K为256。若用head和lnil指针做相对偏移地址，则可以采用1个字节存储。加1运算之后若不考虑溢出，就等价于加1模256操作。

2 映射高斯噪声

为了由均匀噪声快速产生高斯噪声，采用了映射函数法。其算法原理如图2所示。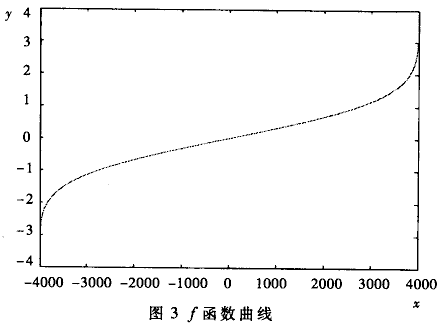

    将正态分布函数的自变量y进行合理的离散化，得到一系列函数值，构成一个数列。再将此数列中的任一个数yi映射到数轴x上的某个小区间段[xi0，xi1]，其中‖xi1－xi0‖=yi。取遍数列中所有的数值，得到一系列的小区间。将所有的小区间依次连接起来，中点置于数轴的零点，则构成变量x的取值区间[-x，x]。将数轴x上的各个小区间与y序列建立映射关系，则可以证明，如果采样间隔足够小，那么x域中的随机分布将对应于y域中的高斯分布。

这个映射关系可以函数表示为y=f（x）。

其中x服从(-X，X)区间内均匀分布，而y服从均值为u、方差为σ的高斯分布。f函数曲线如图3所示。

    在算法实现时，对y对应的高斯分布值进行量化处理，并为x分配一块连续的内存区域[0，2X]，每个内存单元的(偏移地址-X)值代表了x值大小，单元内容存放了该单元对应的丁值。这片内存区域就是所需要的映射查找表。这个表具有通用性，可以预先计算好，在需要时可¨直接使用，不必再计算。

 对于(0，1)正态分布，图4中的zi都小于1，没有实际意义，所以将其放大了200倍；

则原始映射表描述为：

    原始映射表比较大，实际使用时对其做了粗采样。对y对应的高斯分布值进行的量化也没有采用图4中均标准阶梯形式，而是采用了如下粗采样形式：

结果映射表[k]=原始映射表[k·d+d/2]   (2)

其中：采样间隔d=∑yi／M．，量化处理曲线如图5所示。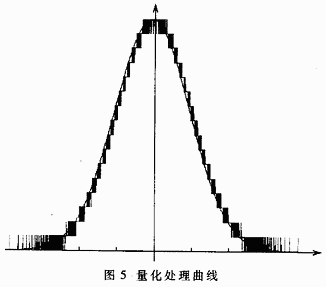

从图5可以发现，两边较小处并没有像阶梯图那样截止为0，而是允许以小的概率出现非零值。试验证明这种方式更好一些。

考虑高斯分布的实际情况，并经过试验验证y仅在[-4，4]之间取值，就能够达到令人满意的精度。图6给出了X大小对噪声精度的影响曲线，纵轴为平均误差。

可以看出，当2X大于5500时，误差达到了极小稳定状态。为了方便计算，选择2X=213=8192，即X=212=4096。

    图7给出了实验结果(均值为120，方差为40)：虚线部分为标准高斯分布的曲线，实线部分为噪声直方图，验证了本方法的有效性。

3 精度讨论

该方法主要利用两个表：一个是循环产生均匀噪声的表；另一个是映射表。这两个表的数值都可以由前面介绍的方法计算，下面只讨论它们的精度取舍。

循环表中256个种子的精度要求与映射表的大小有直接关系，对映射表采用了8192(8K)个单元。因此循环表的任务就是要在区间[-4096，4096]内产生均匀分布的随机数。所以循环表中的种子序列x(1)，…，x(256)在[-4096，4096]内均匀分布。为了方便计算，将种子序列的分布调整到[-(2115-1)，(215-1)]之间，即X=215=32767。所以可以采用包含1位符号位共计16位来存储种子数的补码，这样可以通过丢掉进位的补码加法来实现模X加运算。补码运算结果的高13位或右移3位，可以直接作映射表的偏名地址进行后续查表操作，并且满足在[-4096，4096]内均匀分布。

    考虑实际情况下，待求的高斯噪声分布的方差一般介于(0，100)之间，均值一般介于[-255，255]之间。而实际图像灰度值是以整数[0，255]形式存在，所以噪声的精度只要控制在整数范围内即可，映射表的精度只要达到0．0l就足够了。而映射表中数据的分布介于[-4．00，4．00]之间，若以整数形式存储，将原始数据乘以128后就完全可以存放在16位长度单元中。

也可以在此基础上对表进行修改，使得经过映射后高斯分布的均值和方差直接等于用户给定的均值u和方差σ。修改比较简单，将映射表中的每一个单元值y做如下替换：

y=(y*σ)>>7+u

此表中数据可以是原码形式也可以是补码形式具体需要而定。