

什么是zkSNARK攻击
区块链
描述
早上很多朋友@我,安比实验室发表了一篇文章zkSNARK的“输入假名”的攻击。迅速看了看,很赞。这个攻击原理其实比较简单,但是,不深入理解zkSNARK以及使用场景的朋友确实很难发现和理解。本文讲讲我对这个攻击的分析和理解。
源于三天前
这种攻击方式一直潜伏着,没被发现。直到三天前:

俄罗斯开发者poma,在项目semaphore提交了一个issue,公开了这个攻击方法。poma同时也在kovan测试网络验证了这种攻击方式。
先从semaphore项目的代码开始:
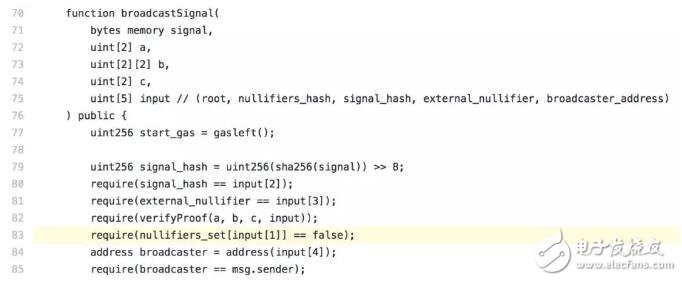
话说,semaphore是个很有意思的项目,它提供了一套方法能让用户不暴露自己身份的情况下广播消息。暂不深入介绍这个项目的内容,直接看函数。broadcastSignal函数提交了证明,某个用户发送某个消息(signal)。只有具体的某个broadcaster(server)才会调用这个函数。
signal - 广播的消息内容
a/b/c以及input - 是zkSNARK的证明以及公开信息(statement信息)
函数实现(第82行),调用verifyProof函数验证证明以及statement信息是否是合理的证明。第83行,查看nullifier_hash是否被用过。
什么是Nullifier?
熟悉ZCash的朋友,估计对Nullifier比较熟悉。
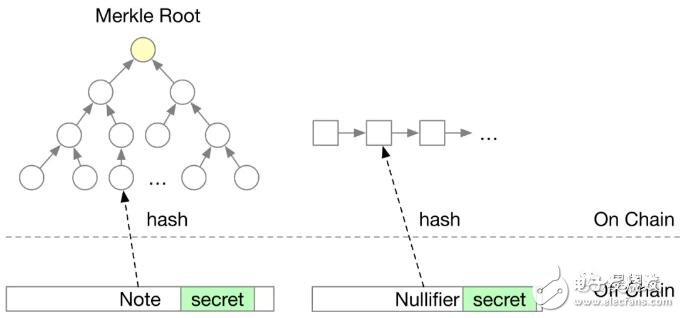
为了保护交易的隐私,在链上只存储Note和Nullifier对应的hash信息。Note代表可以花的钱,Nullifier表示某笔钱已经消费。Note和Nullifier一一对应,一个Note只存在一个Nullifier。通过zkSNARK生成证明,证明Note和Nullifier的正确性以及存在某种联系。在链上,为了防止双花,在执行某个交易时,必须确定某个Note是否已经消费。确定的方法就是记录下Nullifier对应的hash信息。
verifyProof的计算
verifyProof的函数实现在snarkjs项目的templates/verifier_groth.sol(以Groth16为例)。verifyProof只是个简单的wrapper,具体计算的实现时verify函数。
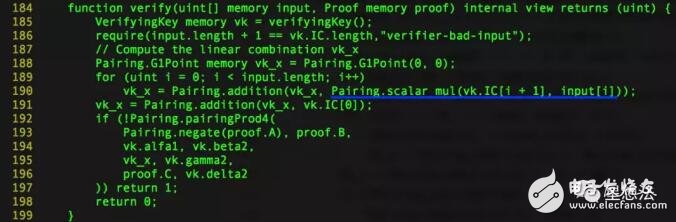
verify就是验证Groth16的验证等式是否成立,再看Groth16的验证等式:

其中橙色部分就是input,蓝色部分就是vk.IC。scalar_mul是椭圆曲线的“标量乘法”计算。vk.IC是椭圆曲线上的一个点(假设为P),input是个标量(假设x)。scalar_mul(P, x) 表示为xP。如果椭圆曲线的阶为q的话,下面的等式成立:
(x+q)P = xP + qP = xP
也就是说,x+p和x作为input的话,scalar_mul的计算结果相等。也就是说,Groth16的等式依然成立。
如何攻击?
在智能合约中,输入input是用uint表示。以太坊上一般采用bn254的曲线,q为:
21888242871839275222246405745257275088548364400416034343698204186575808495617。虽然这个q比较大,但是,uint的最大值还是比q大不少。
攻击方法就形成了:
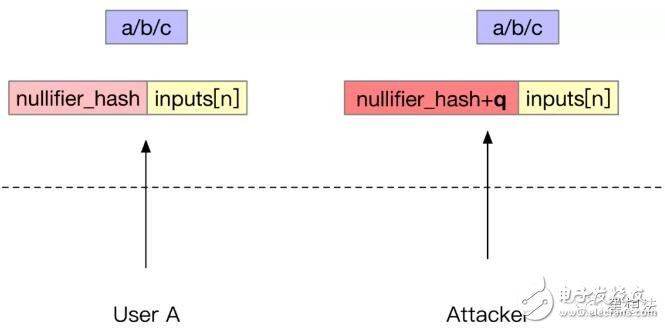
在一个用户提交了证明以及公开的input信息后,攻击者修改input中的nullifier_hash即可。虽然逻辑上在花费同一笔钱,但是,智能合约却认为是花费不同的费用。智能合约认为一个Note只能对应一个Nullfier,事实上,在这样的情况下,一个Note对应了多个Nullfier。
如何修复?
修复的方式有好多种,目前最简单的修复方式是在verify函数加限制:
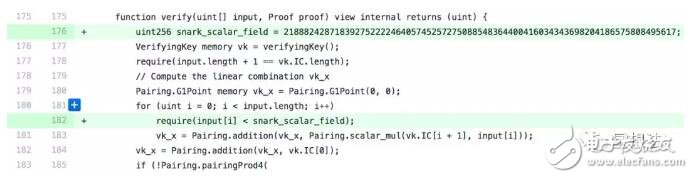
限制input不能超过q。
总结:
三天前,俄罗斯开发者poma公开了zkSNARK应用模型下的一种攻击方式。攻击不需要重新生成证明信息,只需要修改Statement中Nullfier对应的hash数据。原理是,椭圆曲线是个循环群,scalarMul计算在输入的标量加上椭圆曲线的阶的情况下,结果相等。
-
arp攻击如何处理2009-03-12 3973
-
对嵌入式系统的攻击 攻击者通过什么途径得到ATM的密钥呢?2011-08-11 2568
-
最新防攻击教程2012-09-06 2737
-
CC攻击2013-09-10 4290
-
MCU怎么应对攻击与破解?2017-12-21 2751
-
SCDN的抗CC攻击和抗DDoS攻击防护是什么?2018-01-05 4847
-
面对外部恶意攻击网站,高防服务器如何去防御攻击?2019-05-07 1239
-
redis安装过程和模仿攻击模仿攻击2020-03-31 932
-
网络攻击的相关资料分享2021-12-23 1812
-
模板攻击的相关资料推荐2022-01-07 472
-
cc攻击防御解决方法2022-01-22 4035
-
GPU发起的Rowhammer攻击常见问题2023-08-25 630
-
DDOS攻击是什么_ddos攻击攻击是无解的吗2017-12-28 4213
-
dos攻击原理及攻击实例2018-01-17 41177
-
DDoS攻击原理 DDoS攻击原理及防护措施2022-10-20 620
全部0条评论

快来发表一下你的评论吧 !

