容易混淆的4种派克(Park)变换矩阵的基本原理

“由于国内外研究人员对abc坐标系与dq轴的定义不同，造成了Park变换矩阵的多种多样，本文则从4种定义的abc坐标系与dq轴出发，解释了4种Park矩阵的由来”

第一部分 4种派克(Park)变换矩阵的由来

01

—

引言

你见过的Park变换矩阵可能有以下4种形式，另外还有4种对应的形式，只是系数由2/3改为根号下2/3。

你有没有因此而眼花缭乱?有没有因此而不知所措?有没有想弄懂却又求助无门的感觉?有没有不求甚解、得过且过的想法?有没有听之任之、生搬硬套、会用就行的行为？反正我是有过。我很理解这种感受，所以我想将我所了解的内容分享给大家。

今天要分享的内容主要就是4种派克(Park)变换矩阵的基本原理，后续还会介绍Park变换在基于dq轴解耦的双闭环控制中的应用以及一些注意事项。这个知识点比较经典，或者说比较基础，但是确实容易混淆，产生混淆的主要原因是使用Park变换的人来自世界各地，但是他们采用的标准却有所不同，而且应用Park变换的仿真软件也很多，其内置的Park变换模块也不尽相同，新发表的文章或者出版的书籍基本都不会阐述其原理，而是直接使用各种形式的Park矩阵，但是不同Park矩阵的使用都有一定的前提，如果不清楚原理，生搬硬套，可能产生牛头不对马嘴的结果，最终导致仿真结果错误。

由于现有仿真软件中公开一些应用较多的简单实例，我们可以通过软件中的实例去学习Park变换相关的知识点，但是若不能正确的使用好一种仿真软件中的Park变换模块，或者说使用一种软件中的模块时却受到了另一种软件中对应模块的影响，同样地得不到想要的结果，只会越来越自我怀疑，有时甚至会认为某种软件或者文献中的结构是错误的。

这就好比从常德去北京，我们可以选择开车、搭火车或者飞机等等，有很多去北京的方式，但是不能混用和误用工具，我们不能在火车上开汽车，也不能在飞机上开汽车，工具的混误用势必导致我们到不了北京。接下来要介绍的就是怎样认识、区分和利用这些工具，从而不至于得到错误的结果。

02

—

基本原理

2.1  第一种Park变换矩阵

设系统三相电压如式(1)所示。

系统三相电压vabc在abc三相静止坐标系与dq同步旋转坐标系中的关系如图1所示。

图1  第一种abc三相静止坐标系与dq同步旋转坐标系的关系

正常情况下，在abc三相电压中，a相相位超前b相120度，且a相相位超前c相240。在图1-1中，abc三相电压给人的感觉就是，a相相位超前c相120度，且a相相位超前b相240度。其实，abc三相的相序并没有改变，产生上述两种不同情况的原因在于，前一种是通过时间矢量图描述abc三相的关系，而图1是通过空间矢量图描述abc三相的关系，SVPWM中会经常用到空间矢量图，而且我觉得这与物理中描述物体简谐运动的旋转矢量法类似。

由图1可知

结合式(1)和式(2)可得

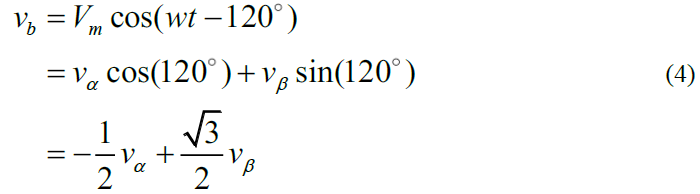
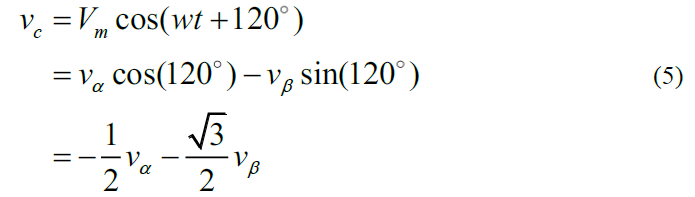
则式(3)至式(5)的关系可得到

Clark变换为：

Clark反变换为：

将dq轴电压向αβ坐标轴投影，可得

则

所以Park变换为：

一般为了使Park矩阵可逆，会引入0轴坐标，且

则

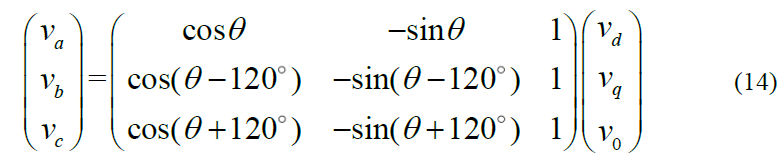
式(14)中为d轴与相位参考轴的夹角，一般取为Ua的相角，后续还会区分怎样由PLL获取Ua的相角，以及是否需要偏移PLL输出角度。

2.2  第2种Park变换矩阵

图2  第二种abc三相静止坐标系与dq同步旋转坐标系的关系

由图2可知，由于abc坐标轴与αβ坐标轴的关系和图1中的关系相同，所以以图2为标准的Clark变换与以图1为标准的Clark变换相同，后面相同的Clark变换则不在叙述。

将dq轴电压向αβ坐标轴投影，可得

则

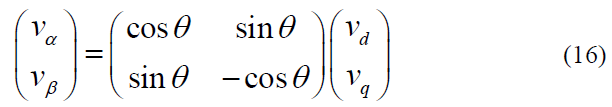
所以Park变换为：

对应Park反变换为：

2.3  第3种Park变换矩阵 

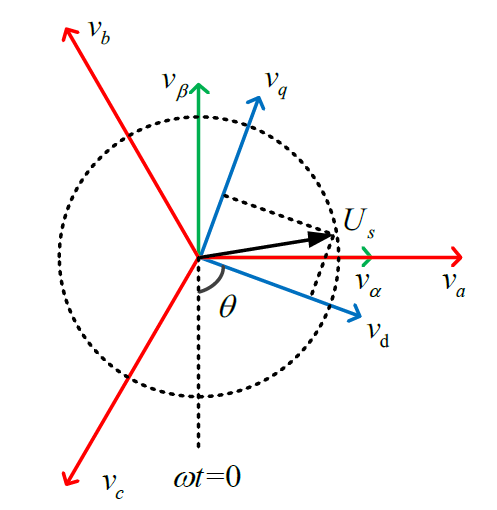
图3  第三种abc三相静止坐标系与dq同步旋转坐标系的关系

将dq轴电压向αβ坐标轴投影，可得

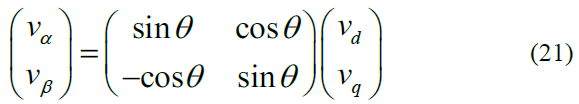
所以Park矩阵为

Park反变换为：

2.4  第4种Park变换矩阵

图4  第四种abc三相静止坐标系与dq同步旋转坐标系的关系

将dq轴电压向αβ坐标轴投影，可得

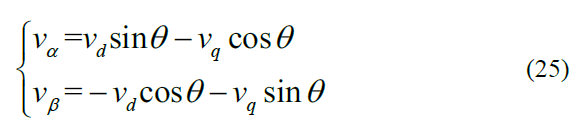
所以Park矩阵为

Park反变换为：

03

—

总结

本文只对Park和Clark的等幅变换进行了简单阐述，其等功率变换同样对应着4种形式，之后有兴趣的话还会阐述。

其实，本文的关键就在于图1至图4，在知道abc三相静止坐标系与dq同步旋转坐标系的4种关系后，想要推导出4种Park矩阵，并弄懂它们之间的区别与联系也就很容易了。

为了便于读者根据文中内容，通过PSCAD或者Matlab进行仿真验证，现给出文中Park矩阵和各软件中模块的对应关系：文中第1种Park变换对应Matlab中abc/dq0模块的第1种Park矩阵；文中第2种Park变换对应PSCAD中abc/dq0模块的Park矩阵；文中第3种Park变换对应Matlab中abc/dq0模块的第2种Park矩阵；文中第4种Park变换暂未找到对应应用。而且第一种和第二种Park矩阵的q轴分量相反，第三种和第四种Park矩阵的q轴分量相反，其值互为相反数，如果有同学想要推导，可以只推导第一种矩阵，后面三种只需要对第一种进行简单的改写即可得到。