

一种基于概率框架的三维点云生成模型PointFlow
电子说
描述
三维点云对于多视角和图形学的表示,合成和重建高质量、高分辨的点云具有重要的意义。虽然近年来在基于点云的判别模型上取得了一系列进展,但在生成模型方面却还存在着诸多挑战。
为了实现对于生成模型的理解和应用,来自康奈尔大学和英伟达的研究人员提出了一种基于概率框架的三维点云生成模型PointFlow,通过为分布的分布建模,分别建立形状的分布和给定形状下点云的分布,来实现对于形状的采样以及给定形状下任意点云的采样过程。

作为三维数据的重要形式,点云由于较高的分辨率和对复杂细节更好的表达越来越受到研究人员的青睐。有效的点云生成模型将为重建和超分辨等点云合成任务带来较大的促进作用。但由于点云复杂的形状使得生成模型的研究较为缓慢,需要利用概率的方式重新审视点云生成模型的学习过程。
例如,一架飞机的点云可以看做是从飞机对应表面上采样而得到的点;而这把飞机的曲面则可以视为从飞机形状的分布中采样得到的一个特定的形状。为了生成点云我们需要对分布的分布进行建模,也就是说不仅需要为形状分布进行建模,同时需要对特定形状下的点云进行建模。
在研究人员提出的PointFlow中,对于形状的分布和给定形状下点的分布进行了建模。
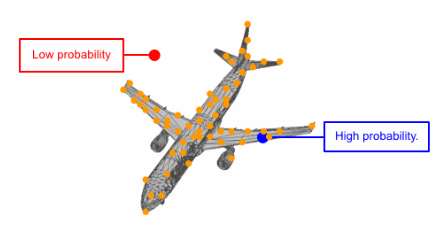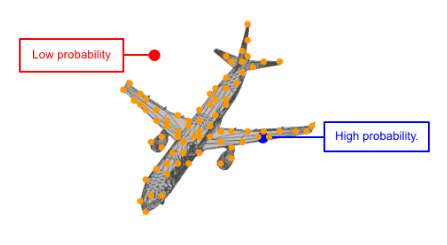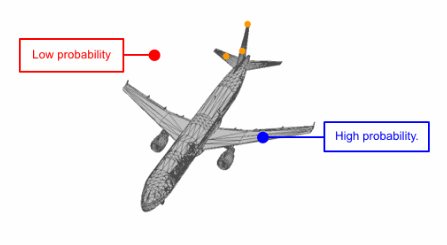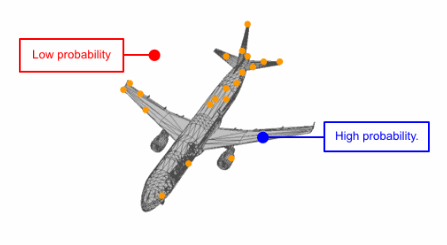
研究人员通过先验分布3D点的可逆参数化变换代替了直接对点云分布的建模。这意味着在给定模型的情况下,首先从通用的高斯先验中进行采样,而后基于参数变换将他们移动到与目标形状对应的新位置,使得参数化的变化和变量的分布都可以利用这一模型进行描述。
更重要的是,这种模型还带来了更强大的表达能力。在可以估计概率密度、提升变分下限的同时,还可以避免由GANs带来的复杂训练。
在三维点云的学习过程中,我们不经需要从某一类的一系列形状中进行形状采样,同时也需要针对某一形状对其表面上的点进行采样(均匀分布)。这一研究的目标在于学习形状的分布和点的分布。研究人员利用连续归一化流(continuous normalizing flow,CNF)来为给定形状下点的分布进行建模。
连续归一化流可以视为三维欧式空间中的向量场,它可以通过对某一通用的先验分布进行转换(例如高斯分布)推导出点云的分布。连续归一化流是一系列可逆的映射,可以将已知的初始化分布映射到更为复杂的分布上去。通过一系列可逆的变换f来表示,这些变换同样可以利用神经网络来实现。

为了从这一推导出的点云中采样,研究人员首先从通用的先验分布中进行采样,然后将这些采样点移动到矢量场(连续归一化流)中去。此外连续归一化流是可逆的,这使得计算精确的似然成为可能。下图展示了一个从先验分布到特定形状点的过程。

随后研究人员利用参数化的方法将每一个归一化流用隐空间变量来进行表示,使得对于形状分布的建模被约化成了对于隐变量的建模。最终的生成模型包含了针对形状和针对点分布的双重连续归一化流。
在训练过程中,得益于连续归一化流的可逆性带来的似然计算,端到端稳定地训练GANs成为可能。训练的过程中需要基于变分自编码器定义三种不同的模块,分别是讲点云编程成形状表示z的编码器Q(z|X)、形状表示的先验P(z)、以及在给定形状表达下为点云分布建模的解码器P(z|X),下图展示了模型的训练和推理过程。

在训练阶段,针对给定的点云X编码器将得到对于形状的后验表示,并从中采样出形状的表示z,随后通过z计算出两方面的损失。一方面利用逆CNF计算出先验分布并与w进行损失计算Lprior;另一方面利用另一个CNF,G的逆计算重建出似然的损失Lrecon。
同时还需要计算后验概率的交叉熵Lent。在测试阶段,利用F和G即可。首先从高斯先验中进行采样并利用F变换到对应的形状表示z上,然后在3D高斯先验上进行采样并基于形状的采样z通过G得到进行转换得到最终的点云。

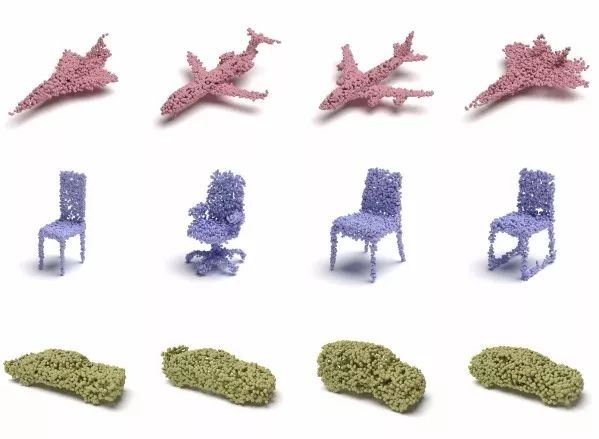
最终利用这种方法生成了一系列点云,可以采样出各种不同的形状,得到任意数量的点云。
下图展示了多个形状的生成过程,首先需要学习出某类形状对应的空间,并从形状空间中得到一个隐变量,随后利用点的CNF,更加隐变量进行转换,最后从归一化分布中采样的点就被转换到了目标形状上了:
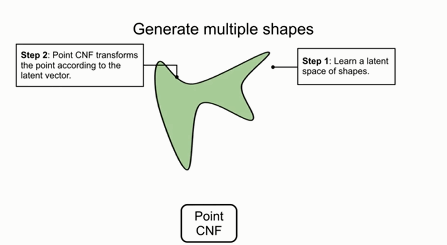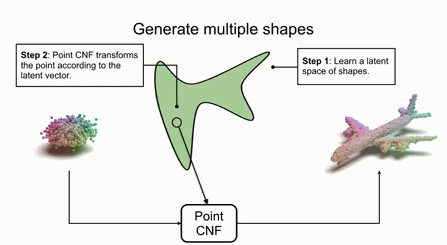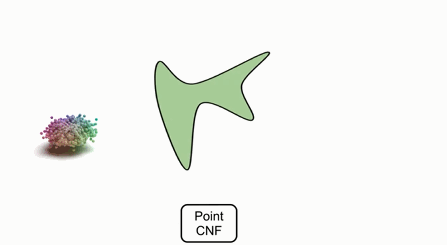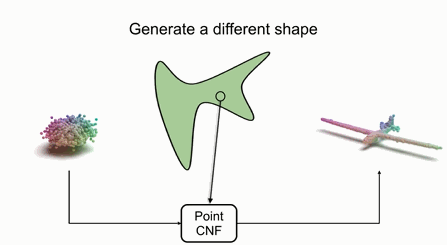
如果需要生成不同的形状,只需要在隐空间中指定不同的隐变量,并对点进行变换即可。
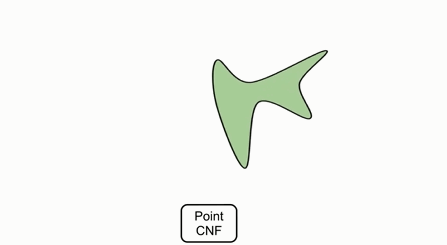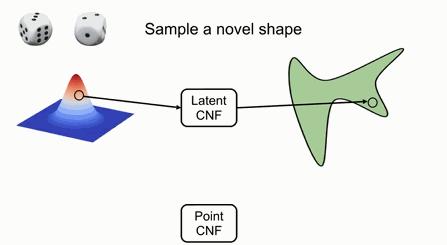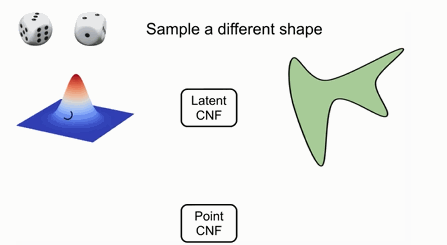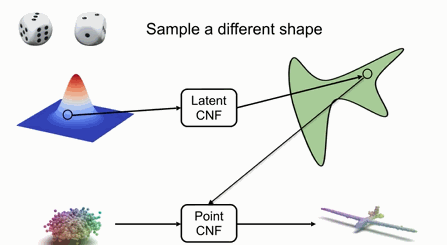
如果要采样出新的形状或不同的形状,可以利用随机变量采样隐空间中CNF,并利用隐空间中对应的变量来对输入的点进行变换。
-
三维快速建模技术与三维扫描建模的应用2018-08-07 3880
-
怎样去设计一种基于RGB-D相机的三维重建无序抓取系统?2021-07-02 2014
-
一种基于等高线生成三维地形的实用方法2009-09-03 732
-
一种简化的三维模糊制器_沈勇2017-03-19 613
-
三维模型的空间匹配与拼接2017-11-22 1569
-
一种新颖的三维模型压缩算法2017-12-25 2117
-
一种三维六度环面Cayley图网络模型2018-01-30 953
-
通过多模态特征融合来设计三维点云分类模型2021-03-11 1432
-
点云的概念以及与三维图像的关系2021-08-17 8438
-
三维点云数据的两种结构Kdtree和Octree2022-03-14 8610
-
介绍一个用于点云生成的概率模型2022-09-09 2703
-
什么样的点可以称为三维点云中的关键点呢?2022-11-22 2272
-
一文详解点云及三维图像处理技术2023-03-31 4344
-
泰来三维|三维扫描服务_三维激光扫描仪测量山体滑坡点云建模2024-05-15 839
-
什么是三维点云分割2024-10-29 1039
全部0条评论

快来发表一下你的评论吧 !

