关于MATLAB 中的机械臂算法分析和介绍

前面，我们讲了机械臂的运动学（kinematics）（点击蓝字查看）：正向运动学和反向运动学。

正向运动学指的是在已知机械臂各个关节角度的情况下，推算end-effector（机械臂终端）的位置和方向（合称pose）。反向运动学指的是在已知end-effector的位置和方向，推算各个机械臂的关节角度。我们主要研究反向运动学。

让我们看一下基于反向运动学的控制逻辑图：

在给出机械臂的end-effector的pose后，反运动学模块计算出各个关节所需要的角度，然后通过电机产生力矩(torque)去执行。在此期间，通过反馈(feedback)去消除一些控制误差。

但是，事实上会有很多的干扰因素存在。例如：

地球引力（gravity）

惯量（inertia）

摩擦力（friction）

科里奥利力和离心力（Coriolis and centrifugal）

由于连杆之间是通过关节（joint）耦合在一起，连杆之间会有反作用力和反向惯量

以及一些人为的要求，例如：

我们想要机械臂运动的速度，按照我们预先的设定运行（velocity and acceleration）

我们想要求机械臂在触碰外物时候做出安全保护（external force）

这些我们暂且称之为disturbance（干扰），当然有些“干扰”是我们故意要求的，比如说需要按照预设轨迹的速度运行。加入“干扰”后的示意图如下：

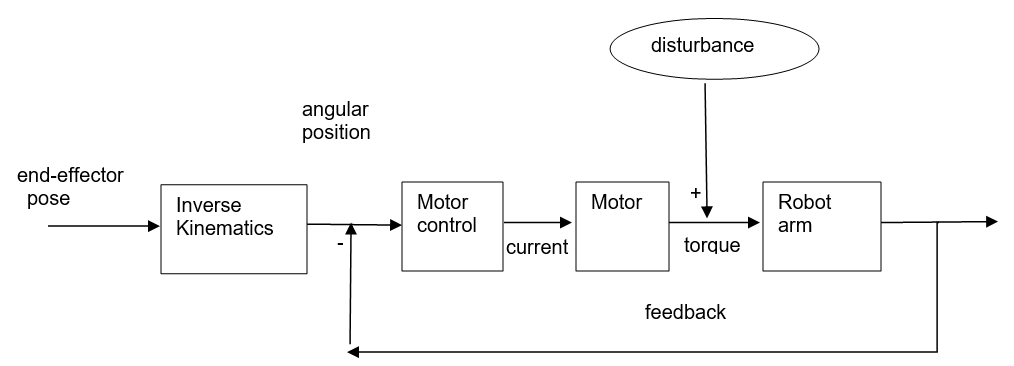
如果我们能提前计算出来这些“disturbance”，然后在控制环路中将它“抵消”（有时候也叫前馈控制）。这样，就能使得机械臂“完美”运行了。让我们再改一下控制逻辑图：

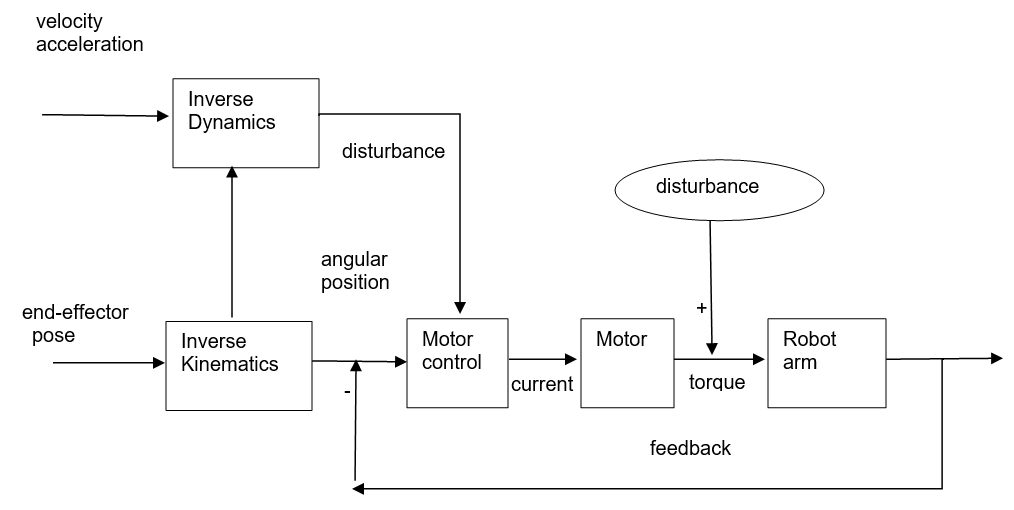
为了计算这些“disturbance”。我们需要考虑几个因素：

机械臂各个关节角度，即q

机械臂各个关节的速度，即qd（对q求导）

机械臂的各个关节的加速度，即qdd（对qd再次求导）

机械臂的质量和各个连杆的重心点

有了这些因素，我们可以通过数学方法：

u=M(q)qdd + C(q,qd)qd +G(q)

求出所需要的力矩，其中M项代表克服了机械臂的加速度惯量以及不同连杆之间的惯量影响所需力矩、C项代表了克服科里奥利力和离心力所需力矩、G项代表了克服地球引力力矩。

其中Inverse Dynamics叫做反向动力学，它的作用是输入想要的关节速度(qd)、关节加速度(qdd)、关节角度(q)，输出为每个关节所需要的力矩（u）。当然也有正向动力学（forward dynamics）,它的作用和反向动力学相反，输入关节角度（q）、关节速度（qd）、每个关节的力矩（u），输出为每个关节的加速度（qdd）。

上述的控制逻辑图，是一个“前馈控制”的例子，它的作用是预先计算出所需的力矩，输入给控制器，“反馈”的存在是为了消除一些误差，例如摩擦力和其他噪音。

总之，我们需要这么一个“动力学”模型，使得我们可以抵消各种不同的“disturbance”的影响 --- 惯量、地球引力、科里奥利力和离心力等等。另外，实际电机的功率是有限的，通过反向动力学我们也可以准确知道电机需要提供多少力矩，从而为电机选型提供参考依据。

下图初略表示了end-effector – inverse kinematics – inverse dynamics之间的关系：

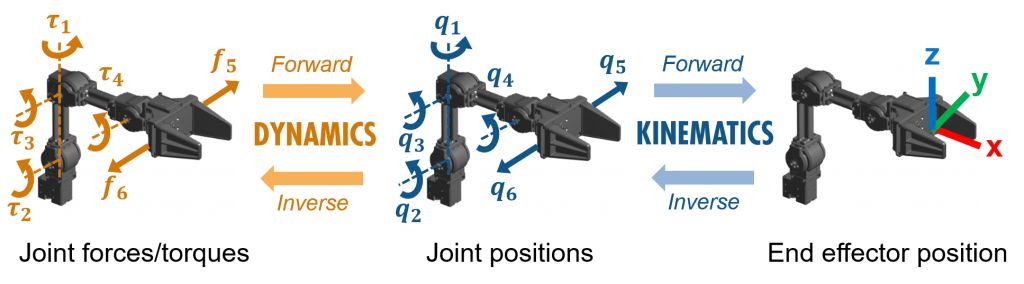
Robotics System Toolbox（RST）中的动力学算法

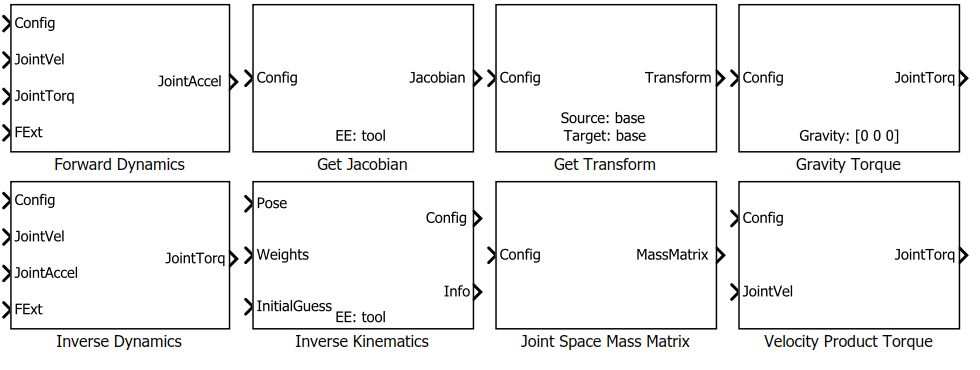
RST 提供了动力学方面的函数和Simulink block。 

MATLAB函数：

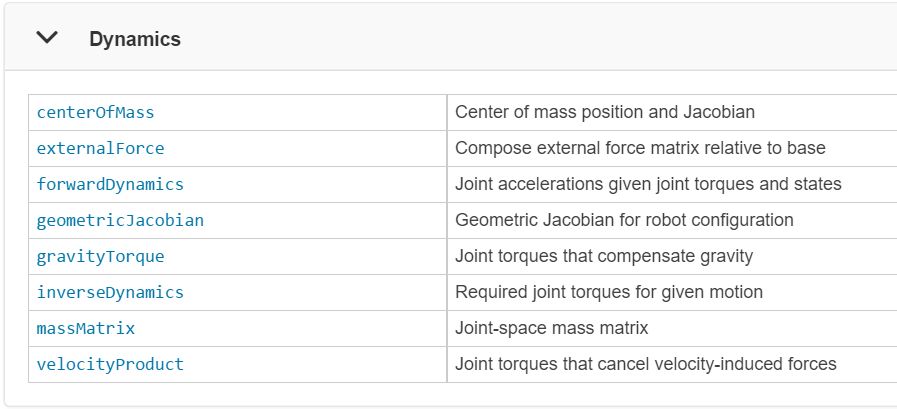
Simulink blocks：

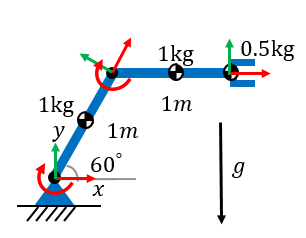
让我们看一个简单的例子： 

这是一个工作在2D空间的机器人。标明了各个结构件的质量、长度和重心。在静止状态下，两个关节分别需要多大的力矩去抵消地球引力并支撑起这个机器人？

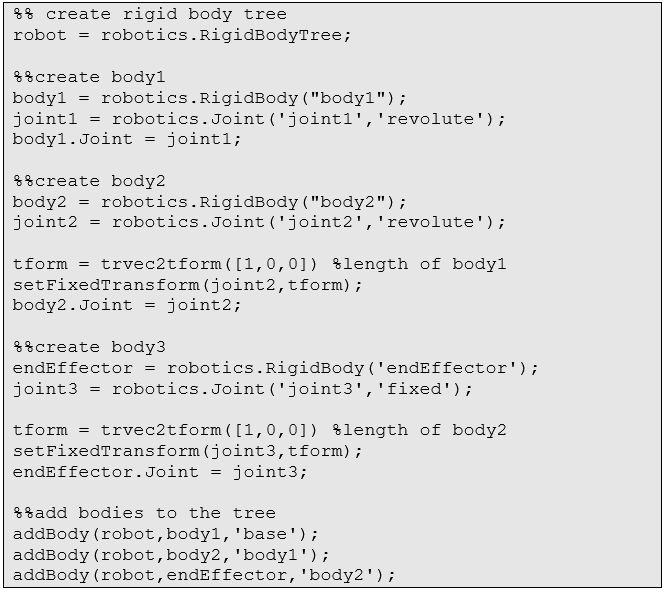
我们先一步步地构造这个机器人：

然后加入重心、质量：

然后在速度和加速度都是0的情况下，调用inverse Dynamics函数算出力矩：

tau =

20    10

很明显，第一个关节要比第二个需要更大的力矩。

我们也可以用gravityTorque这个函数试一下，结果是相同的。

gravTorq =

20    10

如果我们将速度或者加速度改变一下，看看力矩的变化，例如：

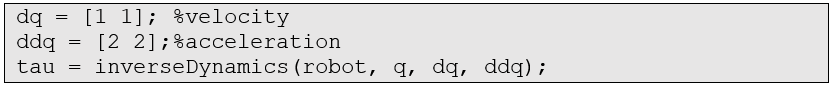
相应地，所需力矩也增大了。

tau =

30.5981   12.1340

Simulink 示例

在MATLAB Central File Exchange上搜索“Designing Robot Manipulator Algorithms”。

这是一个机械臂按运动轨迹抓取物体的例子：

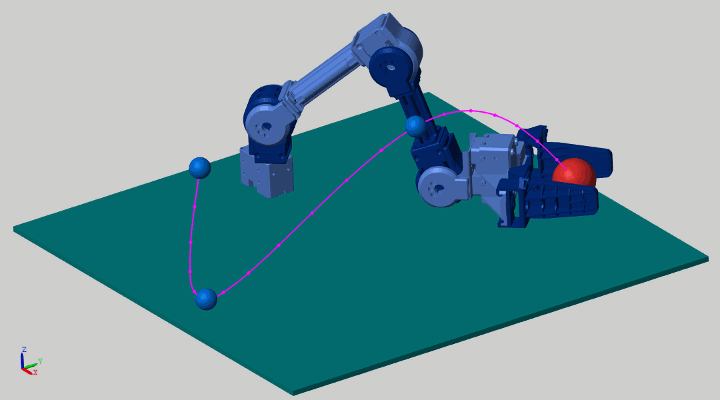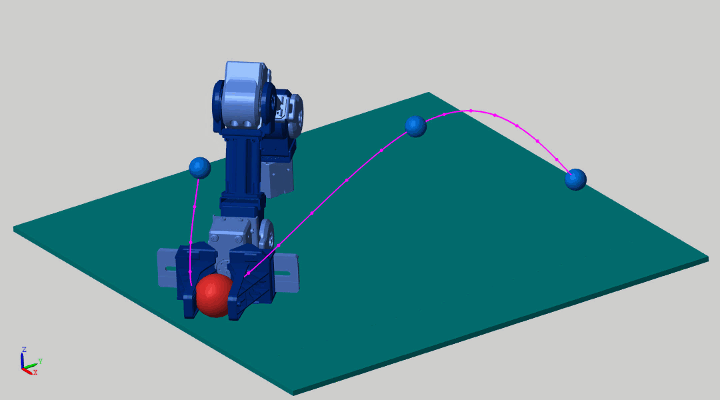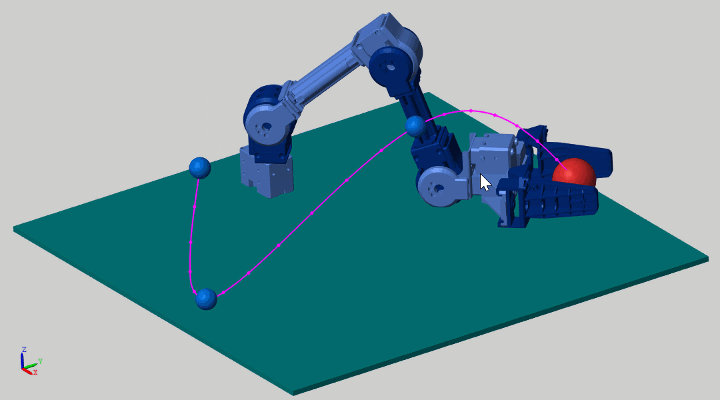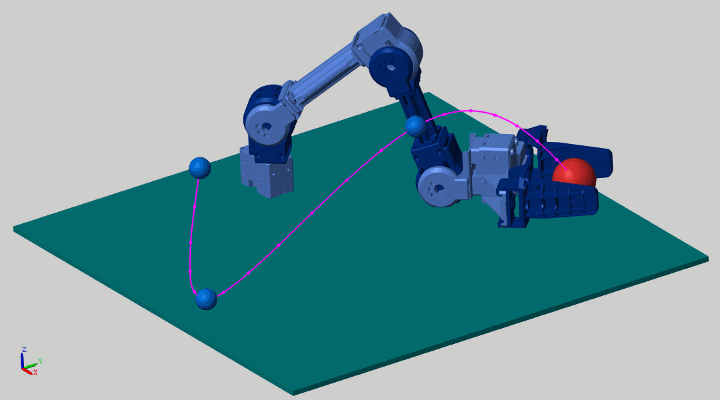
在前面运动学算法中，我们也介绍了这个例子。当时我们用反向运动学（inverse kinematics）去计算end-effector的位置。这次我们用力矩控制的方式来重新看一下这个问题。这里有两种方式供参考：

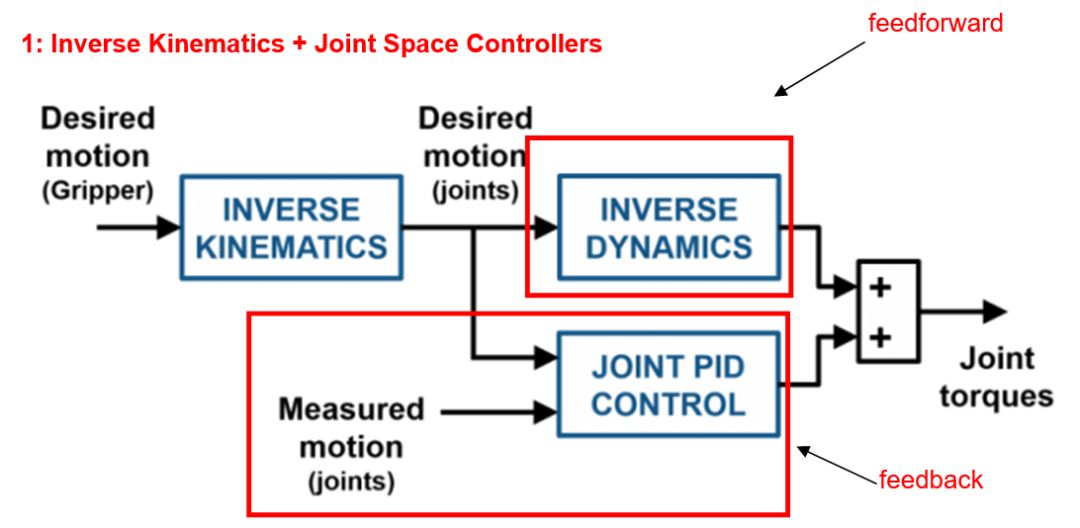
首先，inverse kinematics根据end-effector的位置，计算出各个关节（电机）所需要的角度位置，然后交给各个关节的电机去执行。由于关节控制的是角度。所以叫Joint Space Control （即关节角度控制）。

前馈部分（feedforward）负责计算出所需力矩（用来抵消重力，按预定轨迹运动等等）。

反馈部分（feedback）用PID去消除误差。

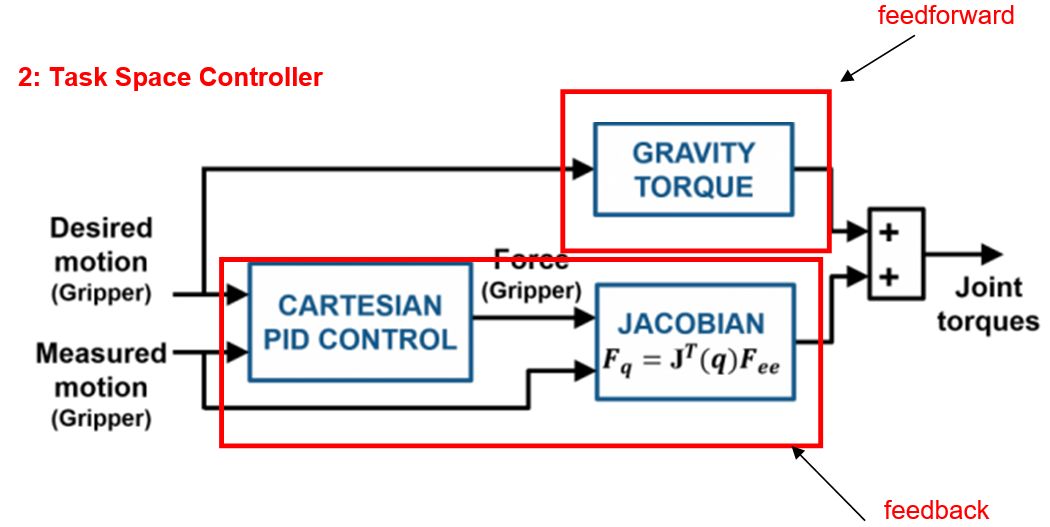
这个做法是直接控制end-effector的位置，并用PID去消除end-effector的位置误差。也叫做task space control，即直接控制在XYZ空间（也叫笛卡尔坐标的位置）。

前馈部分只做一件事：计算抵消地球引力的力矩。

反馈部分用PID去控制end-effector的位置。然后用Jacobian矩阵将end-effector（在笛卡尔坐标）的力矩，转化成各个关节的力矩。

Computed Torque Control

有了机械臂的动力学模型(dynamic model)，我们可以应用的控制方法有很多种。通常来说，反馈是必要的 – 可以消除控制误差和一些噪音。从力矩计算的角度来看，可以做：

力矩前馈控制。刚才两个例子都是将计算好的力矩做前馈。由于机械臂的移动速率远远小于电机控制速率，所以计算力矩的频率并不高。比如说，电机的控制频率为5K Hz，前馈力矩计算的频率大约是50Hz。对控制器的硬件要求不高。

计算力矩控制（computed torque control）。computed torque control工作在较高的控制频率上（例如1K Hz），要比力矩前馈控制频率高的多。对控制器硬件要求较高。

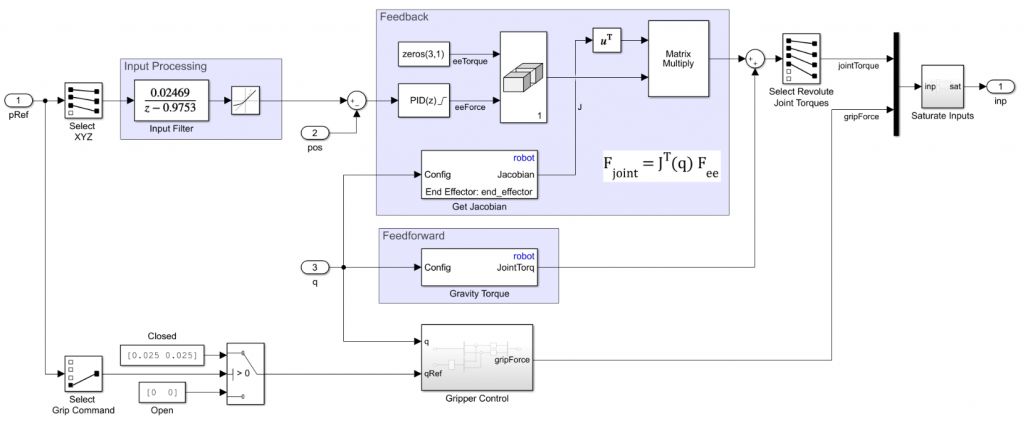
Simulink提供dynamics方面的blocks，可以方便地搭出computed torque controller：

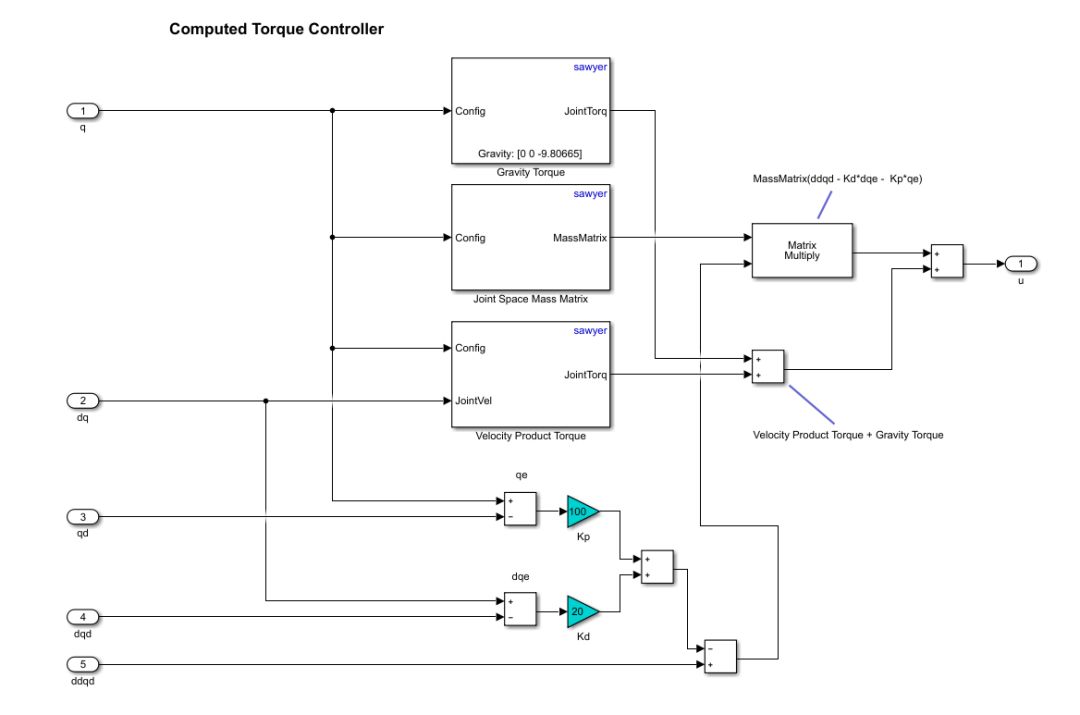
computed torque controller的输入：

q，机械臂关节角度

qd，预设的机械臂关节要达到的角度 (desired q)

dq，机械臂关节速度，即对q求导

dqd，预设的机械臂关节要达到的速度 （desired）

ddqd，预设的机械臂关节要达到的加速度 （desired ）

computed torque controller的输出：

u，机械臂各个关节的力矩

有了computed torque controller我可以做出比较复杂的控制系统，例如一方面要求机械臂按预定的trajectory（含角度、速度、加速度等信息）运行；一方面又要求机械臂遭受外力干扰后改变运行轨迹（trajectory）。

如果感兴趣，可以看MATLAB自带的“Perform Safe Trajectory Tracking Control Using Robotics Manipulator Blocks”这个例子。机械臂在碰到遮挡的硬物，改变预设的运行轨迹，保证运行安全。