使用直方图形式的边缘交叉点数据消除电路抖动

　　在本系列关于抖动历史的前一部分中，我们已经达到了新千年的风口浪尖。当今抖动分析的流行方法是使用直方图形式的边缘交叉点数据，并将高斯函数拟合到图的尾部。但是，正如我们所知，尾巴适合不适合胆小的人。测试方法将如何向前推进以克服这一障碍?

　　正如实际情况一样，抖动分析的情景在该时间范围内正在经历地震变化。首先，数据速率呈螺旋式上升趋势，将信号完整性问题和抖动分析引入最前沿。还有越来越多的数据信号标准(如USB)的使用，这些标准产生了在测试方法中要解决的问题。 或许更重要的是，实时示波器正在逐渐形成。在20世纪90年代早期，实时示波器可能具有几万个数据点的存储深度。到了21世纪初，记忆深度延伸到了大脑中。同时，这些仪器的处理能力正在上升。总的来说，那一代实时示波器开始指明如何处理未来的抖动分析。??尾部拟合的困难源于需要拟合两个参数：随机抖动(Rj( dd))和确定性抖动(Dj(dd))。但是，如果我们已经知道Rj(dd)，那么我们只需要找到Dj(dd)。那么问题就变成了如何将Rj(dd)尾部与Dj(dd)尾部分开。这是实时示波器不断增长的功能成为抖动分析问题的解决方案。??到21世纪初，实时示波器被用于分析和隔离困难的电路问题。在嵌入式系统中，由于能够触发罕见事件或瞬变以及解码串行数据，因此它们是调试的关键。用户能够获取非常长的记录，以确定边缘实际到达的时间并表征抖动。这直接导致了专用串行数据分析仪的出现。??在2000年代，使用实时示波器确定边缘的到达时间有很多进步。有一种算法的演变，旨在分离各种抖动成分。正在采用数据分析技巧来消除数据相关的抖动。有人试图隔离有界不相关抖动的侵入，以及确定周期性抖动分量。

图1：一个例子一个时间间隔错误轨道

在大多数（如果不是全部）这些更好地分析和量化抖动的努力的背后是Dual-Dirac模型本博客系列的上一部分。但是，在20世纪90年代，抖动测量的另一种方法开始扎根：时间间隔误差（TIE）：参见图1.
在其核心，抖动测量是关于边缘实际到达何时到达预期的时间。对于任何给定的边缘，两者之间的差异是其TIE值。如果分析波形中的一堆边并绘制它们，则可以创建TIE轨迹，或者基本上是所有这些TIE值的波形（参见图2）。

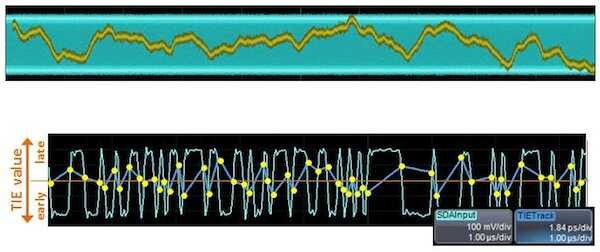
图2：TIE轨道（顶部为黄色）有助于进一步分析缓慢变化的抖动元素

从这些数据中，可以获得其他形式的分析，并且这些形式通过20世纪90年代用于时钟数据恢复的锁相环（PLL）的出现而得以促进。使用USB信号，您只有没有时钟的数据，您必须确定基础比特率。 USB是如何实现PLL的一个很好的例子（与一些应用数学相一致）。芯片开始内置于示波器中，这些示波器将数学和工程技术结合在一起，以根据比特率消除漂移的低频抖动。这有点像听音乐：无论是更快还是更慢，我们都会轻拍我们的脚，但我们会跟踪它。这就是PLL在无时钟信号的时钟恢复中所做的工作。