

AI系统的建立必须估计算法的泛化能力
人工智能
描述
在新数据中,深度学习系统执行(泛化)能力如何?其性能如何?要想建立AI系统的信赖度和可靠性,必须估计算法的泛化能力。我们能信任AI吗?AI是否会像人类酗酒一样毫无顾忌?一但AI启动,是否会毁灭世界?AI系统必须安全可靠,一旦启动AI,算法才能按预期执行。确保AI算法性能良好是提高其采用度和信任度的必由之路 [5]。
此外,决策人在欧盟委员会发布的《可信赖AI的伦理准则》(《ETHICS GUIDELINES FOR TRUSTWORTHY AI》)中明确规定要了解算法的泛化能力。
然而,模型泛化性(泛化理论)研究领域依然投资不足。目前唯一可继续且可行的标准方法是进行数据拆分、验证集和测试集。然而,尽管在无法量化算法的泛化能力时,在测试(留出)集上进行估计不失明智;但这一过程非常棘手,可能发生数据泄漏的风险,需要另外进行独立性假设(独立性验证的参数单独从留出集中选出),但会与p-hacking 等实践所混淆[20]。
数据是由潜在的未知分布D生成的,这是上述工作的关键性假设。统计学习并非直接访问分布,而是假定给出了训练样本S,其中S的每个元素均由D生成,并呈独立同分布。学习算法从函数空间(假设类)H中选择函数(假设h),其中H = {f(x,α)},α是参数向量。
于是,假设h的泛化误差可定义为:从分布D中选取的样本x的预期误差与经验损失(给定样本S上的损失)之间的差值 [4,11]。我们的任务是给泛化错误设定上限,看究竟会出现多么严重的泛化错误。
传统泛化理论中,根据假设类H的复杂度(容量)建立泛化能力模型。简单来说,类的“容量”取决于可以在这个类上拟合良好的数据集的数量。类的容量越大,这个类就越灵活,但也越容易过度拟合。[..]容量控制使用的是更加灵活的模型,以获得良好拟合,那些非常灵活但过度拟合的模型则弃之不用。如何界定假设类H的复杂性?传统泛化理论概念包括VC维、Rademacher复杂度和PAC-Bayes边界。
VC(Vapnik-Chervonenkis)维是一种通过评估函数弯曲程度来衡量函数类的复杂度的一种方式,H类的VC维即可以被H打散的最大样本点数目。如果一组样本点都能被函数打散,无论为一组内所有样本点分配什么样的二进制标签,该类样本都可以将其完美分离。
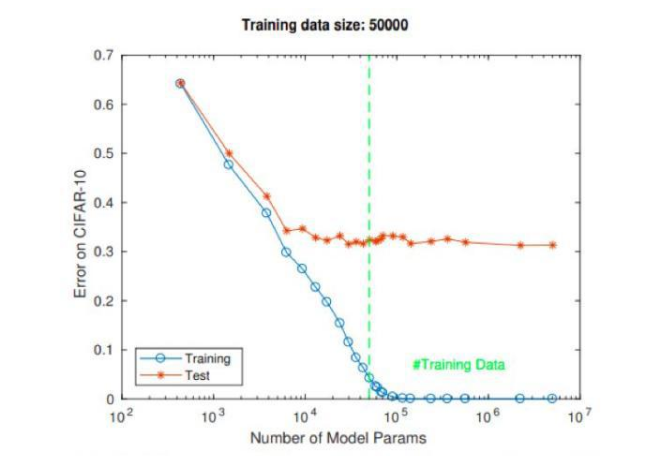
Zhang等人的实验[7]表明,在现实数据中训练的深网真实的“参数复杂度”目前无人知晓,20多年前巴特利特(Bartlett)的VC计算(#节点数*#层)只是一个粗略设定的上限[ 2]。死亡神经元的实验数据表明,当网络足够大,并使用非线性激活函数ReLU时,许多权重为零,这一点可能不足为奇。
PAC(可能近似正确)可学习性的定义很简单,即存在一种算法,对于每个分布D和,δ> 0,找到具有概率1-δ的“-最优”假设。每个分布都有一个算法的呼声十分强烈,即Rademacher复杂度反而针对特定但未知的分布D而定义。简而言之,Rademacher复杂度衡量假设类H的能力,以适应随机±1二进制标签。与VC维相比,Rademacher复杂度取决于分布,可用于任何类别的实值函数(不仅是离散值函数)。
正如Bartlett的VC维计算,Rademacher复杂度缺乏有效的深度学习泛化界限。事实上,实验测试表明,许多神经网络用任意标签完美拟合训练集,于是,我们也希望相应模型H的Rademacher复杂度臻于完美。当然,这只是Rademacher复杂度的一个微不足道的上限,在现实环境中得不到有用的泛化界限[7]。
换句话说,理论研究尚未取得有效成果,只能从“炼金术”或一些最佳实践中寻找解决办法。有实践表明:对Rademacher这种复杂学习架构来说,能够真正降低其复杂度的唯一方法是使用训练分类器,并通过留出集检测缺少的泛化。世界上每一位从业者其实无意中已经做到了这一点。张等人的研究([7])得出的结论目前在该领域无人超越,获得了认同。
与之相关的另一个容量测量是网络的利普希茨常数。利普希茨常数是权值矩阵的谱范数的乘积。谱范数是矩阵的最大奇异值:矩阵可以拉伸一个向量[9]。利普希茨常数与超额风险相关(测试误差减去训练误差)。然而,尽管风险过高,但这一度量随着时间的推移而增长[4];其增长可以通过利普希茨常数的间距抵消掉,重复抵消可使增长归一化(见图4)
泛化的基本定理表明,如果训练集具有m个样本,那么定义为训练数据和测试数据误差间差异的泛化误差是sqrt(N'/ m)的量级,其中N'是网络有效参数的数量 [或复杂度度量] [23,24]。采用具有N个可训练参数的矩阵C,并尝试将其压缩为另一个具有较少参数(N'')的C'和与C大致相同的训练误差。根据泛化基本定理,只要训练样本的数量超过N'',那么C'(压缩网!)就能进行良好的泛化[23,24]。
除了“彩票票据方法”之外,还有很多其他有趣的网络压缩方法。其中一个非常有吸引力的想法受到了TensorNetworks的启发:“Tensor Train”的概念显示了DNN全连接层的权值矩阵,显示出已经很有希望的实证结果[17]。尽管这种压缩通常需要重新训练压缩网络,但[25]提供了对网络压缩方法的调查,这是基于[23,24]提供的基本定理和压缩的泛化理论的方法所没有考虑到的地方。
-
基于空子载波的信噪比估计算法2010-04-23 1889
-
有没有大神会OFDM系统仿真,包含同步算法,LS,LMMSE,SVD等算法的信道估计2016-04-15 4328
-
LCR-TDD系统初始频偏估计算法对比分析哪个好?2021-06-02 1881
-
基于PN序列的频偏估计算法2009-08-19 1443
-
基于IR-UWB的非相干TOA估计算法2010-01-22 797
-
多普勒中心频率实时估计算法2011-06-28 1227
-
OFDM系统中的信道估计算法比较2011-12-07 740
-
基于FFT的高精度频率估计算法2012-02-08 871
-
突发传输的非数据辅助载波频偏估计算法2012-02-09 900
-
基于实信号特点的稀疏表示波达方向估计算法2017-11-10 875
-
基于UMHexagonS的运动估计算法优化2017-11-24 703
-
基于相位补偿的FDOA估计算法2018-02-28 843
-
大华基于AI的场景流估计算法和光流估计算法刷新全球最好成绩2021-01-22 1761
-
面向大规模MIMO系统的信道估计算法2021-06-08 1068
-
信道估计算法2022-12-12 2547
全部0条评论

快来发表一下你的评论吧 !

