零知识证明中的libsnark源代码全面分析

最近一个月发生好多事情。原有的合作关系的结束，新的合作关系的开始。创业变化就是快。期间，我也自己问自己，自己该何去何从？彷徨，犹豫，对未知的未来，我也不确定。但是，内心有种强烈的感觉，告诉自己，有想法，就去干，保持好奇。也许，内心深处，总有一丝侥幸，万一能走出一条路呢。也许，真的就成了呢？

libsnark源代码，建议想深入零知识证明的小伙伴都读一读。Bellman库主要围绕Groth16算法，libsnark给出了SNARK相关算法的全貌，各种Relation，Language，Proof System。为了更好的生成R1CS电路，libsnark抽象出protoboard和gadget，方便开发者快速搭建电路。

本文中使用的libsnark源代码的最后一个commit如下：

commit 477c9dfd07b280e42369f82f89c08416319e24ae

Author： Madars Virza 《[e-mail]》

Date： Tue Jun 18 18:43:12 2019 -0400

Document that we also implement the Groth16 proof system.

1. 源代码目录

源代码在libsnark目录下：

common - 定义和实现了一些通用的数据结构，例如默克尔树，稀疏向量等等。

relations - relation描述了“约束”关系。除了我们通常说的R1CS外，还有很多其他约束的描述语言。

reductions - 各种不同描述语言之间的转化。

knowledge_commit - 在multiexp的基础上，引入pair的概念，两个基点一个系数，计算结果称为一个pair。

zk_proof_systems - 零知识证明中的各种证明系统（包括Groth16，GM17等等）。

gadgetlib1/gadgetlib2 - 为了更方便的构建R1CS，libsnark抽象出一层gadget。已有的gadget，可以方便地整合搭建出新的电路。

2. Relation

需要零知识证明的问题都是NP问题。NP问题中有一类问题NPC（NP-complete）问题。所有的NP问题都可以转化为一个NPC问题。只要有一个NPC问题能多项式时间内解决，所有的NP问题都能多项式时间内解决。描述一个NPC问题，有多种方式。描述NPC问题的方式，称为“language”。Relation指的是一个NPC问题和该问题的解的关系。

libsnark库总结了几种描述语言：

·constraint satisfaction problem类

R1CS - Rank-1 Constraint System

USCS - Unitary-Square Constraint System

·circuit satisfaction problem类

BACS - Bilinear Arithmetic Circuit Satisfiability

TBCS - Two-input Boolean Circuit Satisfiability

·ram computation类

RAM是Random Access Machine的缩写。libsnark总结了两种RAM计算框架：

tinyRAM

fooRAM

· arithmetic program类

QAP - Quadratic Arithmetic Program（GGPR13）

SAP - Square Arithmetic Program（GM17）

SSP - Square Span Program （DFGK14）

先介绍实现各种语言中需要的“variable” （variable.hpp/variable.tcc），再详细介绍R1CS以及QAP语言。

2.1 variable

template《typename FieldT》

class variable {

public：

var_index_t index;

。..

};

varible的定义非常简单，描述一个variable，只需要记录一个varible对应的标号就行了。比如对应编号为index的variable，表示的是x_{index}变量。

2.2 linear_term

linear_term描述了一个线性组合中的一项。线性组合中的一项由变量以及对应的系数组成：

template《typename FieldT》

class linear_term {

public：

var_index_t index;

FieldT coeff;

。..

};

2.3 linear_combination

linear_combination描述了一个完整的线性组合。一个linear combination由多个linear term组成：

template《typename FieldT》

class linear_combination {

public：

std：：vector《linear_term《FieldT》 》 terms;

。..

};

2.4 R1CS

R1CS定义在constraint_satisfaction_problems/r1cs/r1cs.hpp。R1CS约束就是满足以下形式的一个表达式：

《 A ， X 》 * 《 B ， X 》 = 《 C ， X 》

X是所有变量组合的向量，A/B/C是和X等长的向量。《，》代表的是点乘。一个R1CS系统由多个R1CS约束组成。

R1CS约束定义为：

template《typename FieldT》

class r1cs_constraint {

public：

linear_combination《FieldT》 a， b， c;

。..

};

一个R1CS约束，可以由a/b/c三个linear_combination表示。 一个R1CS系统中的所有变量的赋值，又分成两部分：primary input和auxiliary input。primary就是“statement”， auxiliary就是“witness”。

template《typename FieldT》

using r1cs_primary_input = std：：vector《FieldT》;

template《typename FieldT》

using r1cs_auxiliary_input = std：：vector《FieldT》;

一个R1CS系统，包括多个R1CS约束。当然，每个约束的向量的长度是固定的（primary input size + auxiliary input size + 1）。

template《typename FieldT》

class r1cs_constraint_system {

public：

size_t primary_input_size;

size_t auxiliary_input_size;

std：：vector《r1cs_constraint《FieldT》 》 constraints;

。..

}

2.5 QAP

QAP定义在arithmetic_programs/qap/qap.hpp。libsnark采用的QAP的公式是：A*B-C=H*Z。

template《typename FieldT》

class qap_instance {

private：

size_t num_variables_;

size_t degree_;

size_t num_inputs_;

public：

std：：shared_ptr《libfqfft：：evaluation_domain《FieldT》 》 domain;

std：：vector《std：：map《size_t， FieldT》 》 A_in_Lagrange_basis;

std：：vector《std：：map《size_t， FieldT》 》 B_in_Lagrange_basis;

std：：vector《std：：map《size_t， FieldT》 》 C_in_Lagrange_basis;

}

num_variables_表示QAP电路的变量的个数。num_inputs_表示QAP电路的“statement”对应变量的个数。degree_表示A/B/C中每个多项式的阶的个数（和电路的门的个数相关）。

domain是计算傅立叶变换/反傅立叶变换的引擎，由libfqfft库实现。

何为Lagrange basis？

给定一系列的x和y的对应关系，通过拉格朗日插值的方式，可以确定多项式： p（x） = y_0l_0（x） + y_1l_1（x） + 。.. + y_nl_n（x） 其中l_0（x）， l_1（x）， 。.. l_n（x）就称为拉格朗日basis。

A_in_Lagrange_basis/B_in_Lagrange_basis/C_in_Lagrange_basis把一个电路中每个变量不同门的值整理在一起。举个例子，如下是x^3+x+5的电路对应的R1CS的约束：

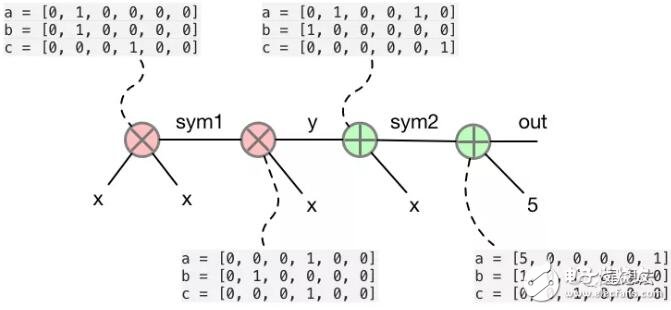
该电路对应的A_in_Lagrange_basis/B_in_Lagrange_basis/C_in_Lagrange_basis为：

qap_instance描述的是一个QAP电路，A/B/C对应的多项式表达式（虽然是用Lagrange basis表示）。A/B/C多项式在一个点上的结果，用qap_instance_evaluation表示：

template《typename FieldT》

class qap_instance_evaluation {

private：

size_t num_variables_;

size_t degree_;

size_t num_inputs_;

public：

std：：shared_ptr《libfqfft：：evaluation_domain《FieldT》 》 domain;

FieldT t;

std：：vector《FieldT》 At， Bt， Ct， Ht;

FieldT Zt;

。..

}

qap_instance_evaluation，记录了在t点上，A/B/C/H以及Z对应的值。

一个QAP电路，对应的primary/auxiliary，称为witness，定义为：

template《typename FieldT》

class qap_witness {

private：

size_t num_variables_;

size_t degree_;

size_t num_inputs_;

public：

FieldT d1， d2， d3;

std：：vector《FieldT》 coefficients_for_ABCs;

std：：vector《FieldT》 coefficients_for_H;

。..

}

coefficients_for_ABCs就是witness。为了计算的方便，同时给出了对应的H多项式的系数。 在给定一个qap_instance_evaluation和一个qap_witness的前提下，可以通过is_satisfied函数确定，是否witness合理：

template《typename FieldT》

bool qap_instance_evaluation《FieldT》：：is_satisfied（const qap_witness《FieldT》 &witness） const

{

。..

ans_A = ans_A + libff：：inner_product《FieldT》（this-》At.begin（）+1，

this-》At.begin（）+1+this-》num_variables（），witness.coefficients_for_ABCs.begin（），witness.coefficients_for_ABCs.begin（）+this-》num_variables（））;

ans_B = ans_B + libff：：inner_product《FieldT》（this-》Bt.begin（）+1，

this-》Bt.begin（）+1+this-》num_variables（），witness.coefficients_for_ABCs.begin（），witness.coefficients_for_ABCs.begin（）+this-》num_variables（））;

ans_C = ans_C + libff：：inner_product《FieldT》（this-》Ct.begin（）+1，

this-》Ct.begin（）+1+this-》num_variables（），witness.coefficients_for_ABCs.begin（），witness.coefficients_for_ABCs.begin（）+this-》num_variables（））;

ans_H = ans_H + libff：：inner_product《FieldT》（this-》Ht.begin（），

this-》Ht.begin（）+this-》degree（）+1，

witness.coefficients_for_H.begin（），

witness.coefficients_for_H.begin（）+this-》degree（）+1）;

if （ans_A * ans_B - ans_C ！= ans_H * this-》Zt）

{

return false;

}

。..

}

检查一个witness是否正确，就是计算wA*wB-w*C = HZ是否相等。

3.Reduction

Reduction实现了不同描述语言之间的转化。libsnark给出了如下一系列的转化实现：

bacs -》 r1cs

r1cs -》 qap

r1cs -》 sap

ram -》 r1cs

tbcs -》 uscs

uscs -》 ssp

以r1cs-》qap为例，梳理一下Reduction的逻辑。从R1CS到QAP的转化逻辑在reductions/r1cs_to_qap/目录中，定义了三个函数：

3.1 r1cs_to_qap_instance_map

r1cs_to_qap_instance_map函数实现了从一个R1CS实例到QAP instance的转化。转化过程比较简单，就是将系数重新整理的过程（可以查看2.5中的QAP的描述）。

3.2 r1cs_to_qap_instance_map_with_evaluation

r1cs_to_qap_instance_map_with_evaluation函数实现了从一个R1CS实例到qap_instance_evaluation的转化。给定t，计算A/B/C以及H/Z。

3.3 r1cs_to_qap_witness_map

r1cs_to_qap_witness_map函数实现了从一个R1CS实例到qap_witness的转化。

template《typename FieldT》

qap_witness《FieldT》 r1cs_to_qap_witness_map（const r1cs_constraint_system《FieldT》 &cs，

const r1cs_primary_input《FieldT》 &primary_input，

const r1cs_auxiliary_input《FieldT》 &auxiliary_input，

const FieldT &d1，

const FieldT &d2，

const FieldT &d3）

在给定primary/auxiliary input的基础上，计算出witness（A/B/C以及H的系数）。d1/d2/d3在计算H系数提供扩展能力。Groth16计算的时候，d1/d2/d3取值都为0。 给定primary/auxiliary input，A/B/C的系数比较简单，就是primary/auxiliary input的简单拼接后的结果。

r1cs_variable_assignment《FieldT》 full_variable_assignment = primary_input;

full_variable_assignment.insert（full_variable_assignment.end（）， auxiliary_input.begin（）， auxiliary_input.end（））;

H多项式系数的计算相对复杂一些，涉及到傅立叶变换/反傅立叶变换。H多项式的计算公式计算如下： H（z） ：= （A（z）*B（z）-C（z））/Z（z）

其中，A（z） ：= A_0（z） + w_1 A_1（z） + 。.. + w_m A_m（z） + d1 * Z（z），B（z） ：= B_0（z） + w_1 B_1（z） + 。.. + w_m B_m（z） + d2 * Z（z），C（z） ：= C_0（z） + w_1 C_1（z） + 。.. + w_m C_m（z） + d3 * Z（z）， Z（z） = （z-sigma_1）（z-sigma_2）。..（z-sigma_n）（m是QAP电路中变量的个数，n是QAP电路门的个数）。特别强调的是，A（z）/B（z）/C（z） 是多个多项式的和，并不是每个变量对应的多项式。

1/ 确定A和B的多项式（通过反傅立叶变换）

for （size_t i = 0; i 《 cs.num_constraints（）; ++i）

{

aA［i］ += cs.constraints［i］.a.evaluate（full_variable_assignment）;

aB［i］ += cs.constraints［i］.b.evaluate（full_variable_assignment）;

}

domain-》iFFT（aA）;

domain-》iFFT（aB）;

2/ 计算A和B，对应FieldT：：multiplicative_generator的计算结果

domain-》cosetFFT（aA， FieldT：：multiplicative_generator）;

domain-》cosetFFT（aB， FieldT：：multiplicative_generator）;

3/ 确定C的多项式（通过反傅立叶变换）

for （size_t i = 0; i 《 cs.num_constraints（）; ++i）

{

aC［i］ += cs.constraints［i］.c.evaluate（full_variable_assignment）;

}

domain-》iFFT（aC）;

4/ 计算C，对应FieldT：：multiplicative_generator的计算结果

domain-》cosetFFT（aC， FieldT：：multiplicative_generator）;

5/ 计算H，对应FieldT：：multiplicative_generator的计算结果

for （size_t i = 0; i 《 domain-》m; ++i）

{

H_tmp［i］ = aA［i］*aB［i］;

}

for （size_t i = 0; i 《 domain-》m; ++i）

{

H_tmp［i］ = （H_tmp［i］-aC［i］）;

}

domain-》divide_by_Z_on_coset（H_tmp）;

6/ 计算H多项式的系数（反傅立叶变换）

domain-》icosetFFT（H_tmp， FieldT：：multiplicative_generator）;

4. ZK Proof System

libsnark提供了四种证明系统：

·pcd （Proof-Carrying Data）

·ppzkadsnark （PreProcessing Zero-Knowledge Succinct Non-interactive ARgument of Knowledge Over Authenticated Data）

·ppzksnark （PreProcessing Zero-Knowledge Succinct Non-interactive ARgument of Knowledge）

·zksnark （Zero-Knowledge Succinct Non-interactive ARgument of Knowledge）

著名的Groth16算法，属于ppzksnark。因为Groth16在证明之前，需要预处理生成CRS。ppzksnark证明系统又可以细分成好几种：

其中：

r1cs_gg_ppzksnark，gg代表General Group，就是Groth16算法。

r1cs_se_ppzksnark，se代表Simulation Extractable，就是GM17算法。

r1cs_ppzksnark，就是PGHR13算法。

以Groth16算法（r1cs_gg_ppzksnark）为例，梳理一下相关的逻辑。Groth16算法的相关逻辑在zk_proof_systems/ppzksnark/r1cs_gg_ppzksnark目录中。

4.1 r1cs_gg_ppzksnark_proving_key

r1cs_gg_ppzksnark_proving_key记录了CRS中在prove过程需要的信息。

template《typename ppT》

class r1cs_gg_ppzksnark_proving_key {

public：

libff：：G1《ppT》 alpha_g1;

libff：：G1《ppT》 beta_g1;

libff：：G2《ppT》 beta_g2;

libff：：G1《ppT》 delta_g1;

libff：：G2《ppT》 delta_g2;

libff：：G1_vector《ppT》 A_query;

knowledge_commitment_vector《libff：：G2《ppT》， libff：：G1《ppT》 》 B_query;

libff：：G1_vector《ppT》 H_query;

libff：：G1_vector《ppT》 L_query;

r1cs_gg_ppzksnark_constraint_system《ppT》 constraint_system;

。..

}

A_query是A（t）以G1生成元的multiexp的计算结果。

B_query是B（t）以G1/G2生成元的multiexp的计算结果。

H_query是如下的计算以G1位生成元的multiexp的计算结果：

H（t）*Z（t）/delta

L_query是如下的计算在G1位生成元的multiexp的计算结果：

（beta*A（t）+alpha*B（t）+C（t））/delta

也就是说，r1cs_gg_ppzksnark_proving_key给出了Groth16算法中CRS的如下信息（用蓝色圈出）

r1cs_gg_ppzksnark_constraint_system《ppT》定义在zk_proof_systems/ppzksnark/r1cs_gg_ppzksnark/r1cs_gg_ppzksnark_params.hpp文件中。

template《typename ppT》

using r1cs_gg_ppzksnark_constraint_system = r1cs_constraint_system《libff：：Fr《ppT》 》;

也就是说，r1cs_gg_ppzksnark_constraint_system就是r1cs_constraint_system。

4.2 r1cs_gg_ppzksnark_verification_key

r1cs_gg_ppzksnark_verification_key记录了CRS中在verify过程需要的信息。

template《typename ppT》

class r1cs_gg_ppzksnark_verification_key {

public：

libff：：GT《ppT》 alpha_g1_beta_g2;

libff：：G2《ppT》 gamma_g2;

libff：：G2《ppT》 delta_g2;

accumulation_vector《libff：：G1《ppT》 》 gamma_ABC_g1;

。..

}

也就是说，r1cs_gg_ppzksnark_verification_key给出了Groth16算法中CRS的如下信息（用蓝色圈出）

4.3 r1cs_gg_ppzksnark_processed_verification_key

r1cs_gg_ppzksnark_processed_verification_key和r1cs_gg_ppzksnark_verification_key类似。“processed“意味着verification key会做进一步处理，验证的过程会更快。

template《typename ppT》

class r1cs_gg_ppzksnark_processed_verification_key {

public：

libff：：GT《ppT》 vk_alpha_g1_beta_g2;

libff：：G2_precomp《ppT》 vk_gamma_g2_precomp;

libff：：G2_precomp《ppT》 vk_delta_g2_precomp;

accumulation_vector《libff：：G1《ppT》 》 gamma_ABC_g1;

。..

}

4.4 r1cs_gg_ppzksnark_keypair

r1cs_gg_ppzksnark_keypair包括两部分：r1cs_gg_ppzksnark_proving_key和r1cs_gg_ppzksnark_verification_key。

template《typename ppT》

class r1cs_gg_ppzksnark_keypair {

public：

r1cs_gg_ppzksnark_proving_key《ppT》 pk;

r1cs_gg_ppzksnark_verification_key《ppT》 vk;

。..

}

4.5 r1cs_gg_ppzksnark_proof

众所周知，Groth16的算法的证明包括A/B/C三个结果。

template《typename ppT》

class r1cs_gg_ppzksnark_proof {

public：

libff：：G1《ppT》 g_A;

libff：：G2《ppT》 g_B;

libff：：G1《ppT》 g_C;

。..

}

4.6 r1cs_gg_ppzksnark_generator 给定一个r1cs_constraint_system的基础上，r1cs_gg_ppzksnark_generator能生成r1cs_gg_ppzksnark_keypair，也就是生成CRS信息。

template《typename ppT》

r1cs_gg_ppzksnark_keypair《ppT》 r1cs_gg_ppzksnark_generator（const r1cs_gg_ppzksnark_constraint_system《ppT》 &cs）;

4.7 r1cs_gg_ppzksnark_prover

给定了proving key以及primary/auxiliary input，计算证明的A/B/C结果。

template《typename ppT》

r1cs_gg_ppzksnark_proof《ppT》 r1cs_gg_ppzksnark_prover（const r1cs_gg_ppzksnark_proving_key《ppT》 &pk，

const r1cs_gg_ppzksnark_primary_input《ppT》 &primary_input，

const r1cs_gg_ppzksnark_auxiliary_input《ppT》 &auxiliary_input）;

已知proving key的情况下，计算A/B/C的结果，相当简单：

/* A = alpha + sum_i（a_i*A_i（t）） + r*delta */

libff：：G1《ppT》 g1_A = pk.alpha_g1 + evaluation_At + r * pk.delta_g1;

/* B = beta + sum_i（a_i*B_i（t）） + s*delta */

libff：：G1《ppT》 g1_B = pk.beta_g1 + evaluation_Bt.h + s * pk.delta_g1;

libff：：G2《ppT》 g2_B = pk.beta_g2 + evaluation_Bt.g + s * pk.delta_g2;

/* C = sum_i（a_i*（（beta*A_i（t） + alpha*B_i（t） + C_i（t）） + H（t）*Z（t））/delta） + A*s + r*b - r*s*delta */

libff：：G1《ppT》 g1_C = evaluation_Ht + evaluation_Lt + s * g1_A + r * g1_B - （r * s） * pk.delta_g1;

4.8 r1cs_gg_ppzksnark_verifier

总共提供了四种验证函数，分成两类：processed/non-processed 和 weak/strong IC。processed/non-processed是指验证的key是否processed？weak/strong IC指的是，是否input consistency？Primary Input的大小和QAP的statement的大小相等，称为strong IC。Primary Input的大小小于QAP的statement的大小，称为weak IC。

以r1cs_gg_ppzksnark_verifier_strong_IC为例，在给定verification key/primary input的基础上，可以验证proof是否正确。

template《typename ppT》

bool r1cs_gg_ppzksnark_verifier_strong_IC（const r1cs_gg_ppzksnark_verification_key《ppT》 &vk

总的来说，Groth16的证明生成和验证的逻辑如下图：

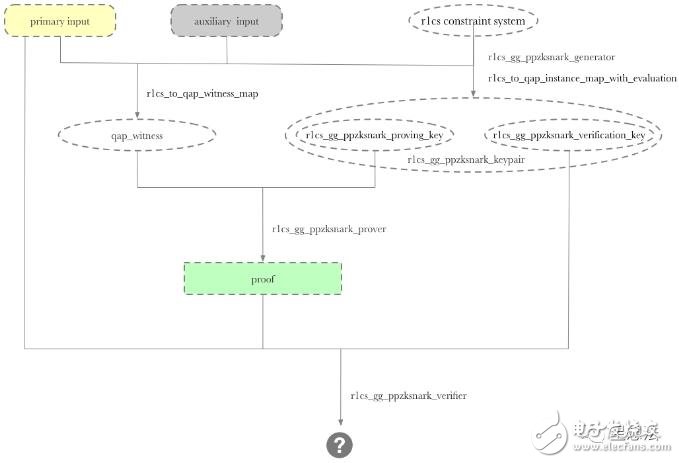
可以看出，使用ZKSNARK（Groth16）证明，需要先创建一个r1cs_constraint_system。libsnark设计了Gadget的框架，方便搭建r1cs_constraint_system。

5. Gadget

libsnark提供了两套Gadget库：gadgetlib1和gadgetlib2。libsnark中很多示例是基于gadgetlib1搭建。gadgetlib1也提供了更丰富的gadget。本文也主要讲解gadgetlib1的逻辑。gadgetlib1的相关代码在libsnark/gadgetlib1目录中。

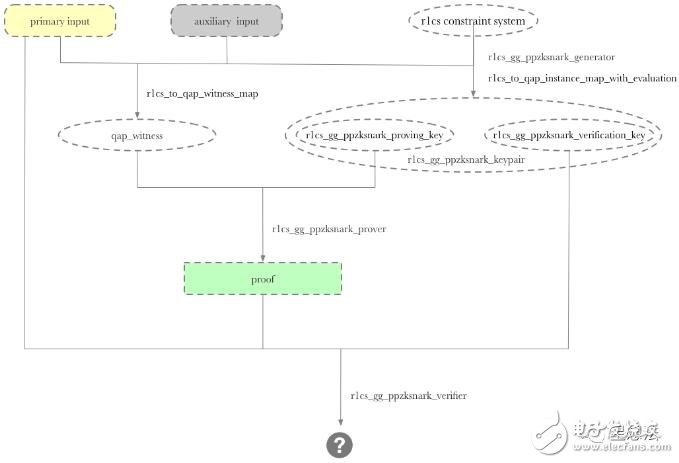
5.1 protoboard

protoboard是r1cs_constraint_system之上的一层封装。通过一个个的Gadget，向r1cs_constraint_system添加约束。为了让不同的Gadget之间采用统一的Variable以及Lc，protoboard通过”next_free_var”以及“next_free_lc“维护所有Gadget创建的Variable以及Lc。