统计灵敏度应该怎样使设计可制造

     “在制造环境中，您的放大器设计没有性能：它只有性能统计数据。”

简介

使用当今的计算机和商业CAD软件包，现在可以在产品开发的初始设计和优化阶段全面解决制造参数问题。这一突破的一些明显好处是：

• 我们设计了一种更具可制造性的产品
• 我们消除（或至少减少）设计和制造之间昂贵的迭代周期
• 我们的设计可靠性

统计灵敏度是用于可制造性设计的关键指标。它被定义为屈服因子直方图的斜率。降低统计敏感度可提高产品产量，并使设计更具可制造性。 RF，微波和高速数字电路由于需要高性能和严格的规格，通常对元件和寄生值具有固有的灵敏度。由于在制造过程中不能精确控制元件值和寄生效应，因此在初始设计中管理这些灵敏度及其相互作用对于可制造产品的设计变得越来越重要。

制造过程中遇到两种类型的故障：

• 灾难性故障 - 由于设备中的物理问题导致的故障，例如焊点不良和材料故障。
• 参数故障 - 由于在制造或使用寿命期间遇到参数变化而导致故障。

我们在此仅考虑参数故障。

当前设计

典型的当前设计过程如图1所示。制造业的特点是参数值不确定，可以产生测试时单元中的参数故障。

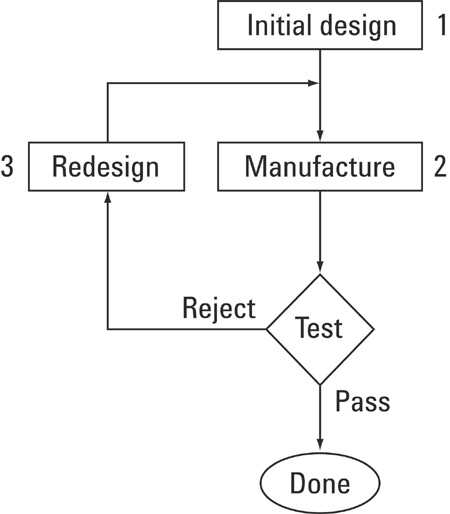
图1 - 当前设计

过程中参数故障太多 - 制造测试需要重新设计和另一次制造尝试。

制造设计（DFM）
使用DFM（也称为统计设计），我们为设计工程师配备测试和制造环境模型（图2）。结合使用这些模型的专业CAD工具，设计工程师可以更好地将设计融入制造过程中遇到的参数环境中，在产品开发的设计阶段。

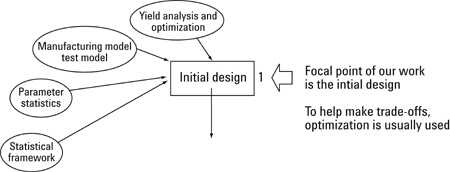
图2 - 制造设计

统计设计技术和CAD软件可以对敏感的射频和微波设计进行表征和减敏，并将其集中在他们的制造环境。

统计设计

可制造的设计在整个范围内提供可接受的性能，并在制造过程中遇到参数值的组合。

统计设计的方法如图3所示。在这种方法中有四个主要步骤：

• 步骤1 - 开发和单点优化设计
• 步骤2 - 执行统计分析以确定性能统计数据
• 步骤3 - 确定性能统计数据是否可接受并获取统计变量之间的任何统计敏感度
• 步骤4 - 如有必要，统计优化并重新分析产量

步骤1是传统的性能优化设计，通常是设计过程的结束。单点优化可找到一组参数值，这些参数值可提供“最佳”性能。 DFM流程需要良好的第1步设计。

在第2步中，我们将统计变量（统计模型）分配给在制造过程中会发生变化的所有参数。然后，CAD软件包通过估计由于参数变化（统计模型）引起的性能变化（性能统计）来执行统计分析。第3步，评估设计的统计性能，是本文的重点。

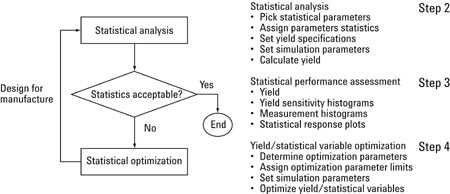
图3 - 制造设计

统计设计优化了设计的性能统计。

可制造性措施

有许多统计指标可以表征制造业绩设计，包括性能均值，标准差和方差，以及像Tagucci S/N这样的更复杂的测量。但是在统计设计中最有用的通用度量是收益率。产量定义为：

统计设计的目标是实现高产量设计。

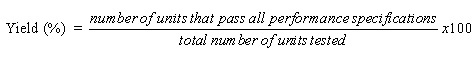
我们现在将讨论用于评估设计统计性能的三个重要统计数据显示。所有这些都可以在今天的CAD软件包中找到。

测量直方图，MH

测量直方图是数字的直方图（或百分比）测量值的出现与测量值的百分比。测量直方图给出了在统计分析期间遇到的测量值的扩展。图4给出了一个例子。

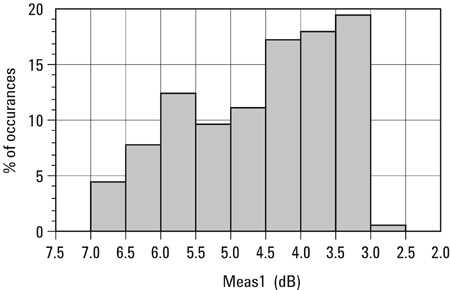
图4 - 测量直方图

MH可以帮助您设置设计规格获得可接受的屈服值。只需将规格设置为包含所需的测量百分比即可。这可能在产量优化开始时是必要的。

统计响应图，SRP

统计响应图是统计模拟期间遇到的所有响应的图。通常将响应相对于自变量绘制，例如S11与频率。 SRP给出了由于定义的统计参数变化而发生的响应变化的度量。统计响应图的一个例子如图5所示。

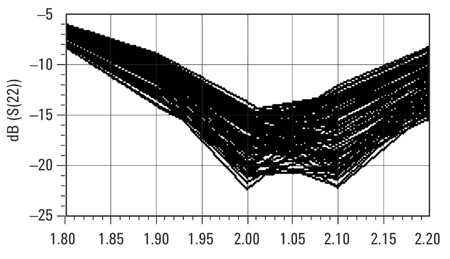
图5 - 统计响应图

统计响应图显示可能的测量变化类型，因为给出了单位参数的统计变化。

屈服灵敏度直方图，YSH

屈服灵敏度直方图是垂直轴上的屈服“图”，而横轴是电路参数的（阶梯式）值。

在所有统计数据显示中，YSH是通常最有用的是因为它显示哪些参数会影响设计的产量以及如何可能更改参数以提高产量。

屈服灵敏度直方图可以指示设计是否处于最大产量（a 居中设计）或设计是否需要进行产量优化（未中心设计。）屈服灵敏度直方图还告诉设计师de中的哪些参数符号影响设计产量，需要包含在产量优化中。

示例YSH如下图6所示。垂直轴（0-100）是以百分比表示的屈服，水平轴（30-42）是给定组件的参数值范围。

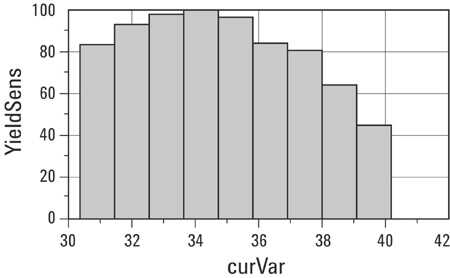
图6 - A产量灵敏度直方图

解释产量灵敏度直方图

YSH是产量与您的设计参数值之间的关系图。绘制的参数值不被认为是统计变量，但是允许所有其他参数根据其指定的统计分布而变化。当参数在其允许的变化范围内步进时，计算每个步骤的产量。

YSH是估计产量与每个阶梯参数值的关系图。例如，参见图6，当curVar（一个元件，如电容或电感）固定在32时，估计的电路良率约为95％。当curVar固定为40时，估计产率为44％。

YSH绘图轴上使用的下限和上限是统计参数的上限和下限。

如果YSH基本上是平坦的，则参数在较低的范围内限制（LL）到上限（UL）不会影响设计的产量。如图7（d）所示。在这种情况下，我们说参数居中。

可能没有必要在yield yield中包含此参数，因为此参数（在其当前范围内）对yield没有影响。也可以在不降低产量的情况下增加该参数的容差。

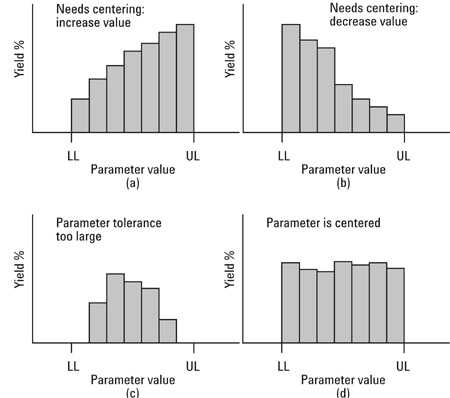
图7 - 如何使用屈服灵敏度柱状图

如果YSH倾斜，如图7（a）和（b）所示，参数会影响屈服值，我们说参数不居中。将参数的标称值移动到更高的产量值可能会增加设计的总产量。

YSH中的每个矩形称为bin。每个箱的高度是使用来自模拟试验的测量值的产量估计，其中参数值在箱底部所覆盖的区间内。应计算每个箱高的置信区间。

如果YSH在中心位置较高而在极端处较低，如图7.3（c）所示，则需要上限和下限（UL和LL）待调整。参数变化的程度是其容差，在这种情况下，参数容差应该减小。

统计敏感度

看着在图8中的屈服灵敏度直方图中，统计灵敏度是直方图的斜率。 YSH具有较大斜率的参数，如图8所示，被认为是一个统计上敏感的参数。

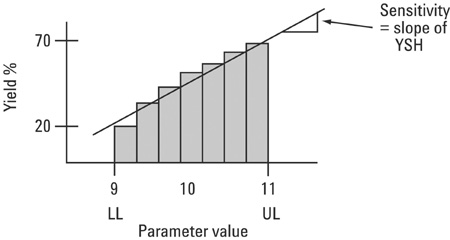
图8 - 统计灵敏度

因为每个箱高代表一个产量估算，所以使用少量试验的YSH可能粗糙且不稳定。这是由于数值估计误差造成的。真实的产量与参数图总是平滑的函数。

统计灵敏度降低

图9显示了统计灵敏度降低的概念，这是设计居中的本质。

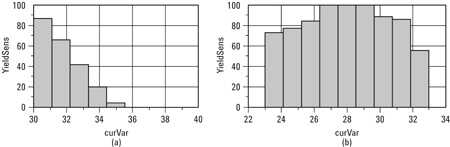
图9＆＃151; （a）设计居中前的YSH，（b）设计居中后的YSH

从图9（a）中我们看到参数标称值（YSH的中心）为35＆＃937;并且当参数值高于36＆＃937;收益率为零。随着参数值从35＆＃937减小，产量增加。从这个YSH的斜率，我们看到对该参数值有很大的统计敏感性。

统计优化后，该参数的YSH如图9（b）所示。在产量优化（设计中心）之后，我们看到这个参数的YSH在任一方向都没有主导斜率，我们说这个参数是居中。（从9（b）可以看出YSH减少了在28和＃937;的标称值的两个方向上。因此，减小该参数的公差将增加产量。）对应于9.5（a）的估计产量约为25％，而对应于9.5（b）的估计产量约为86％。

归一化统计敏感度（NSS）定义为：

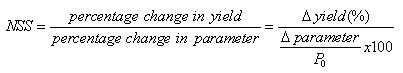
对于图中的YSH 8，NSS是：

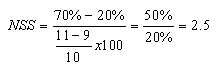
因此，参数值增加（NSS为正）1％会增加产量减少2.5％。您需要了解设计中每个统计参数的统计灵敏度。

示例：低噪声放大器

电路和初始单点设计和优化来自ADS 2001功率放大器设计指南示例部分（LNA_prj）。一个晶体管电路如图10所示。

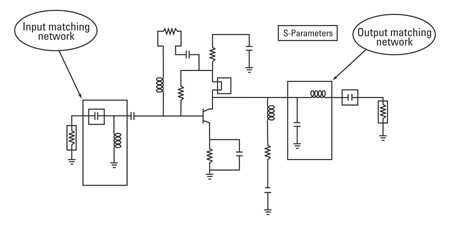
图10＆＃151;突出显示匹配电路的LNA示例电路

该电路的初始设计和优化规范如下：

• 3 V电源，2mA集电极电流
• 2 GHz时噪声系数尽可能低
• 2 GHz时S21> 10 dB
• S11和S22 <-10 =“”db =“”at =“” 2 =“”ghz =“”>
• 无条件稳定

按照惯例，初始设计流程如下：

• 选择晶体管
• 设计偏置网络，确定稳定性
• 添加稳定网络
• 确定晶体管的输入和输出阻抗
• 设计输入匹配电路
• 设计输出匹配电路
• 模拟响应
• 单点优化设计

由于使用单点优化满足所有规范，通常这是设计过程结束的地方。但最重要的是还要确定设计的统计性能。

LNA的统计分析

按照图3中给出的统计设计步骤，我们进行统计分析，然后优化此设计。

1。选择统计参数。选择输入和输出匹配结构以具有统计变量。匹配结构在图10中突出显示。

2。分配参数统计信息。统一+/- 10％分布分配给每个匹配的组件参数。统计模型的选择直接影响估计的屈服值。但统计敏感度并不受统计模型选择的强烈影响。因此，这个简单的模型将有效识别和降低该电路的统计灵敏度。

3。设置良品率规格。产量规格设定为：

• 3 V电源，2mA集电极电流
• S21> 2 GHz时8 dB
• S11和S22 <-6.5 =“”db =“”at =“”1.8ghz =“”> <2.2 =“”ghz =“”>
• 无条件稳定

最初没有考虑噪声系数规格。

4。计算产量。使用500次试验计算得到的收率为91％。

5。检查YSH的所有统计参数。图11和图12显示输入和输出匹配组件参数（C2，L2（输入）和C3，L3（输出））的YSH。

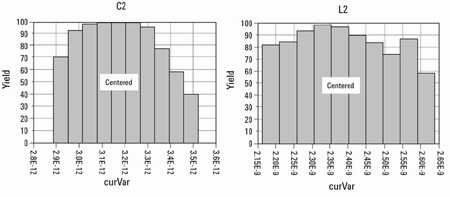
图11＆＃151;输入匹配的统计分析，YSH

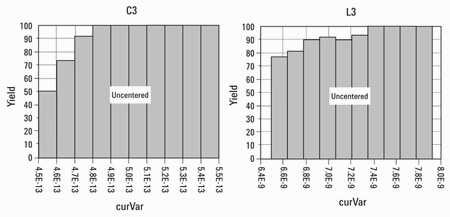
图12＆＃151;输出匹配的统计分析，YSH

很容易看出，描述输入组件C2和L2的参数是居中的，而描述输出组件C3和L3的参数不是居中的。

6。估计统计敏感度。从图11和12中得到的归一化统计灵敏度在表1中给出。

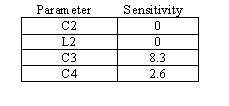表1＆＃151;图11和12中的归一化统计灵敏度

7。执行产量优化。由于在输出匹配参数中检测到统计灵敏度，因此执行了产量优化。此外，使用ADS2001，现在可以进行编程优化。这里首先对输入进行良率优化，然后对输出进行优化，然后对整个电路进行整体最终良率优化。

8。执行产量分析，验证优化结果。输出匹配的结果如图13所示。得到的收益率为100％。此时，可以收紧屈服规格，以确定这种以设计为中心的设计中的任何其他灵敏度。

测量直方图（MH）将帮助您查看此设计的新统计性能，并将根据需要帮助您设置新规格。产量优化前后的参数值如表2所示。

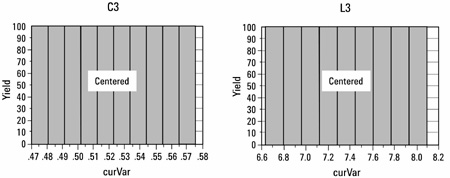
图13 - 产量优化后的YSH图
表2 - 设计居中之前和之后的参数值

LNA示例讨论

我们从一组针对一组参数值的性能进行优化的设计开始：单点优化设计。我们看到这种设计虽然性能高，但产量并不高。通常就是这种情况。

单点优化设计通常不是高产量设计。统计分析和设计对于优化产量等统计性能是必要的。

使用当前的CAD软件可以很容易地完成图3中给出的统计设计步骤。

结论

当今CAD软件的突破使设计工程师能够轻松有效地将制造的参数变化纳入初始设计过程。这里提出的关键点是：

• 统计分析，包括最小化统计敏感性，将导致更可制造的设计。
• 单点优化可能会导致设计中出现不必要的统计敏感度。小心！
• 产量灵敏度直方图显示设计中的统计灵敏度，有助于确定是否需要产量优化。
• 归一化统计灵敏度可量化参数的统计灵敏度。
• 产量优化可提高产量并最大限度地降低统计敏感度。
• 统计设计工具目前可在商业设计平台上使用。

词汇表

组件 - 电路元件，如R，L或传输线。
参数 - 定义组件值的数字：对于电容器，如57pF。单位 - 像放大器或振荡器一样的设计目标。
性能 - 单位的计算或测量响应，如S11，S22，S21和群延迟的组合。
可制造性 - 单位性能对制造过程中遇到的统计参数变化的敏感性。标称参数值 - 用于描述组件的单个参数值，如果参数是统计变量，通常是参数平均值。容差 - 制造过程中参数变化的程度。单点设计 - 最大化单个参数值的单位性能。
统计设计 - 通过参数最大化性能统计统计模型 - 分配给a的概率分布参数，数学上或一组测量值。
CAD - 计算机辅助设计。

参考文献

ADS 2001功率放大器设计指南参考手册，第9章.M。 Meehan和J. Purviance，微波电路和系统设计的产量和可靠性，Artech House，1993。 Purviance，蒙特卡罗统计设计方法，IEEE MTT-S 2001.国际微波研讨会研讨会和短期课程，WMB：微波CAD的统计设计和建模技术。 Purviance和M. Meehan，“用于提高产量的灵敏度图”，IEEE Trans。微波理论与技术，Vol。 1988年2月36日第2期，第413-417页。

博士。 John Purviance，行业顾问，帮助他的客户理解和使用CAD产量分析和优化工具来设计高产量微波和高速数字电路。他在高收益设计，统计灵敏度降低和统计建模方面拥有20年CAD经验，并在高产量设计领域撰写了30多篇技术论文。可以通过[e-mail]与他联系。