

一文知道什么是节点分析和依赖源
描述
节点分析
节点分析是一种分析形式,它使用基尔霍夫电流定律(KCL)和节点方程来求解电路电压值,其中原理图没有任何导体路径交叉。通常用于此目的的术语称为平面电路。
这用于确定每个节点(或两个或多个组件的连接点)的电压尊重参考节点。参考节点通常称为地,其中地电压等于零伏。
在查看电压源或电流源的示意图时,参考节点通常是当为电流源示出箭头时,将其分配给电压源的负端子和相对端。选择参考节点的另一种方法是在查看所有节点时选择中间节点。
有两种电源:1)独立和2)依赖。
独立源为连接的电路提供固定的电压或电流值。独立的来源是电源和电池。电源提供恒定的固定值,而电池在没有充电的情况下不会提供恒定的固定值。
从属源是电压源或电流源,其值取决于根据电路中其他地方的电压或电流值。相关源是分析放大器的有用工具。放大器的两个特性是电压增益(A V )和电流增益(Ai)。有四种基本的线性相关来源:
1。输出为V的电压控制电压源,A V 是比例常数(电压增益),V CD 是被检测的参数。以下等式与压控电压源相关:
$$ V = A_ {V} V_ {CD} $$
2。电流控制电压源,其中输出为V,R M 是比例常数(电阻),I C 是被感测的参数。以下等式与电流控制电压源相关:
$$ V = R_ {M} I_ {C} $$
3。电流控制电流源,其中输出为I,Ai是比例常数(电流增益),I C 是被感测的参数。以下等式与电流控制电流源相关:
$$ I = A_ {I} I_ {C} $$
4。输出为I的压控电流源,GM是比例常数(电导),VCD是被检测的参数。以下公式与压控电流源相关:
$$ I =(G_ {M})(V_ {CD})$$
如图1所示,当有两个直流电压源和一个直流电流源时,会发生一个依赖源的节点分析。注意,E1的值用未知值表示。 E1 = 2Vx。注意,电阻器R1两端的电压表示为Vx。注意,电阻器R3两端的电压表示为V0。此信息稍后将用于计算节点电压。
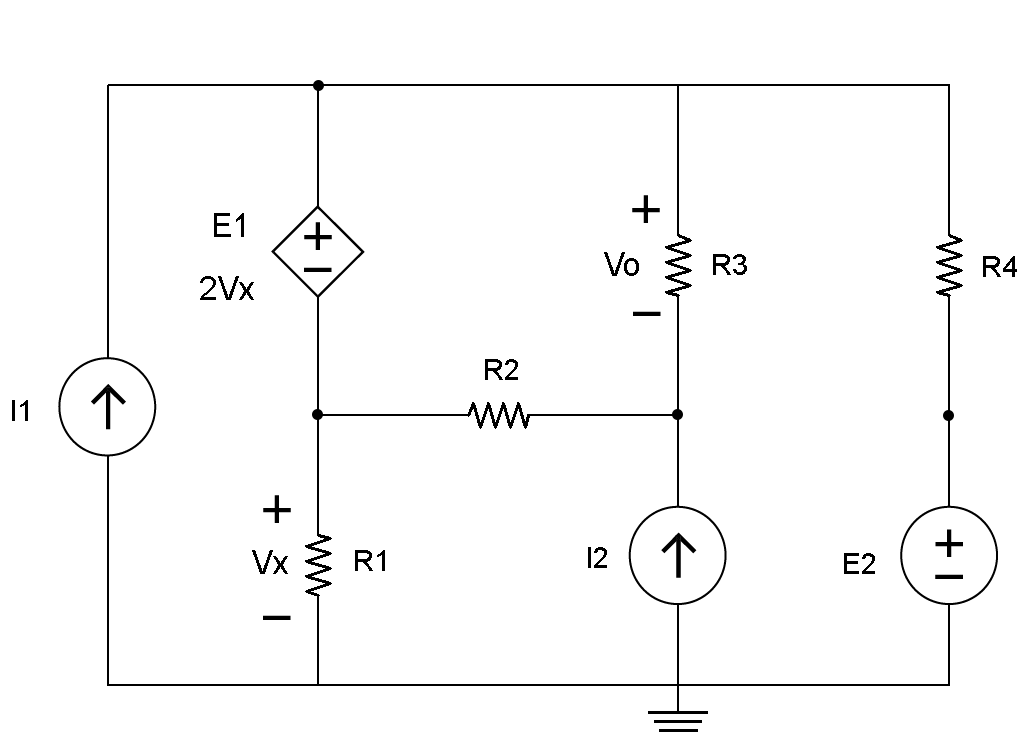
图1
如果节点或测试点电压为正,它将读取电压表上的正值。如果节点或测试点电压为负,它将读取电压表上的负值。
图1所示电路的一个示例问题是找到以下内容:
一个。电阻R3两端的电压(V0)。
B.电流通过电阻R1(IR1),R2(IR2),R3(IR3)和R4(IR4)。
C.设I1 = 2 mAmps,I2 = 2 mAmps,E1 = 2Vx,E2 = 4 V,R1 = 1 Kilo欧姆,R2 = 2千欧,R3 = 3千欧,R4 = 4千欧。
d。设R1(ER1)上的电压= Vx,E1 = V1 - V2。
第一步是识别参考节点或地面,然后是所有节点。图1中显示了电路。通常任何独立的源都接地,如图1所示。
在这个电路中,DC电压源顶部的节点标记为V1,标记为V1,低于E1在标记为V3的电阻器R3下方,以及在标记为V4的DC源E2上方。这些节点如图2所示。
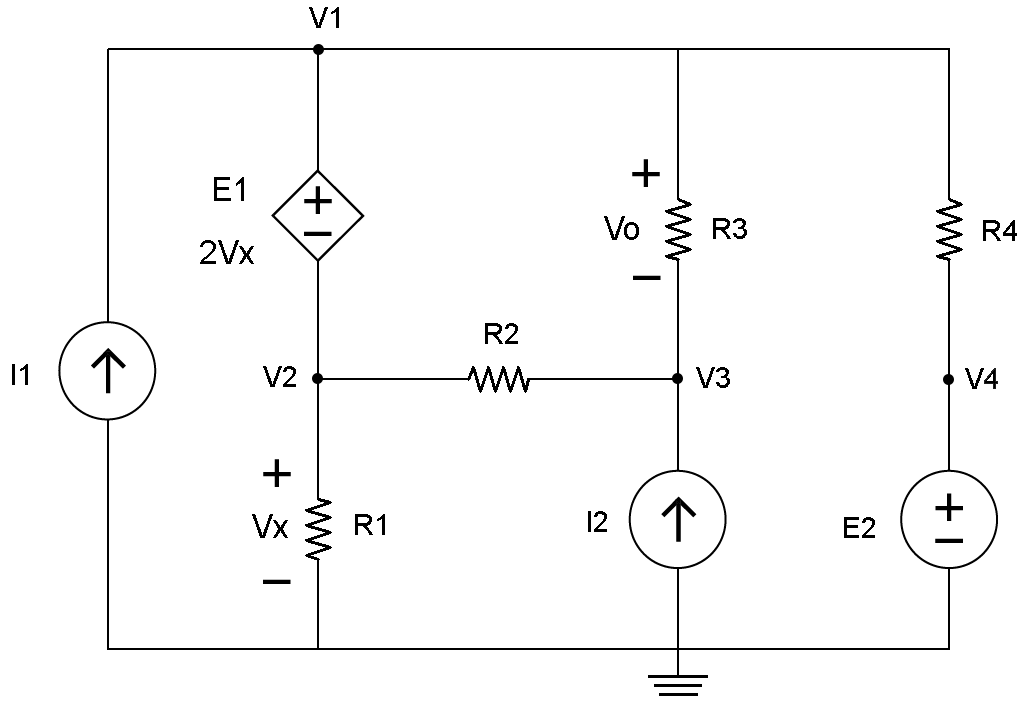
图。 2
第二步是识别超级节点,该节点的从属源具有未知的E1值,等于2Vx。在V1和V2周围绘制一条红线,其中E1如图3所示。
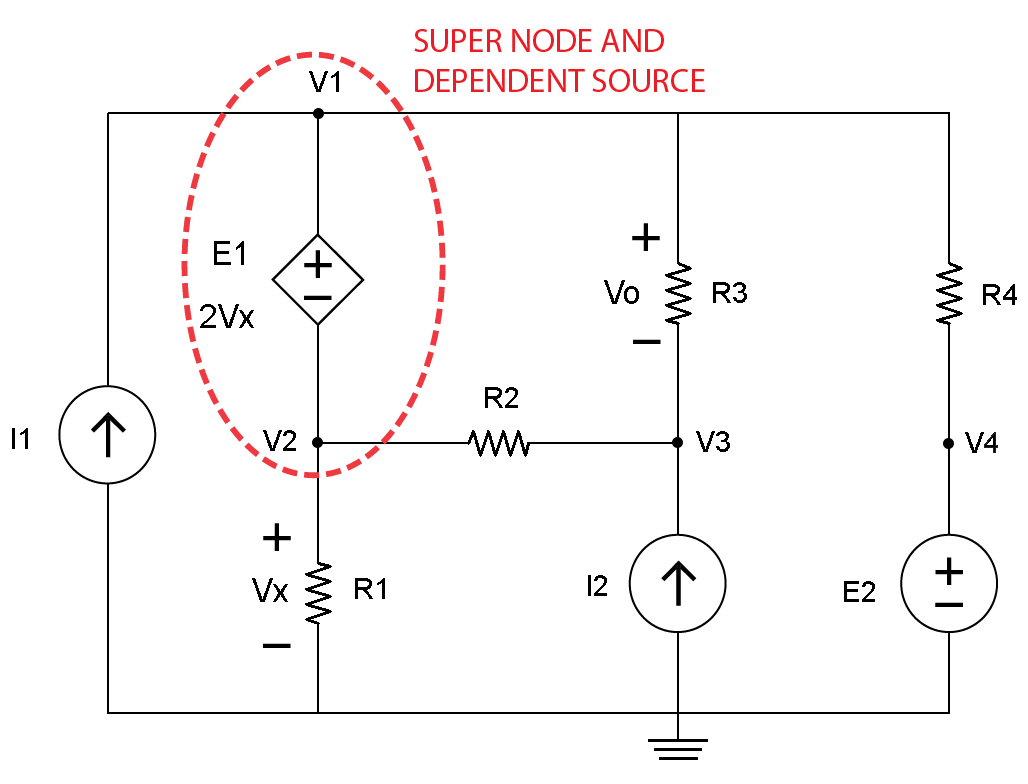
图。 3
第三步是确定独立源,即电压源E2,以及电流源I1和I2。在V4和E2,I1和I2周围画一条蓝线,如图4所示。
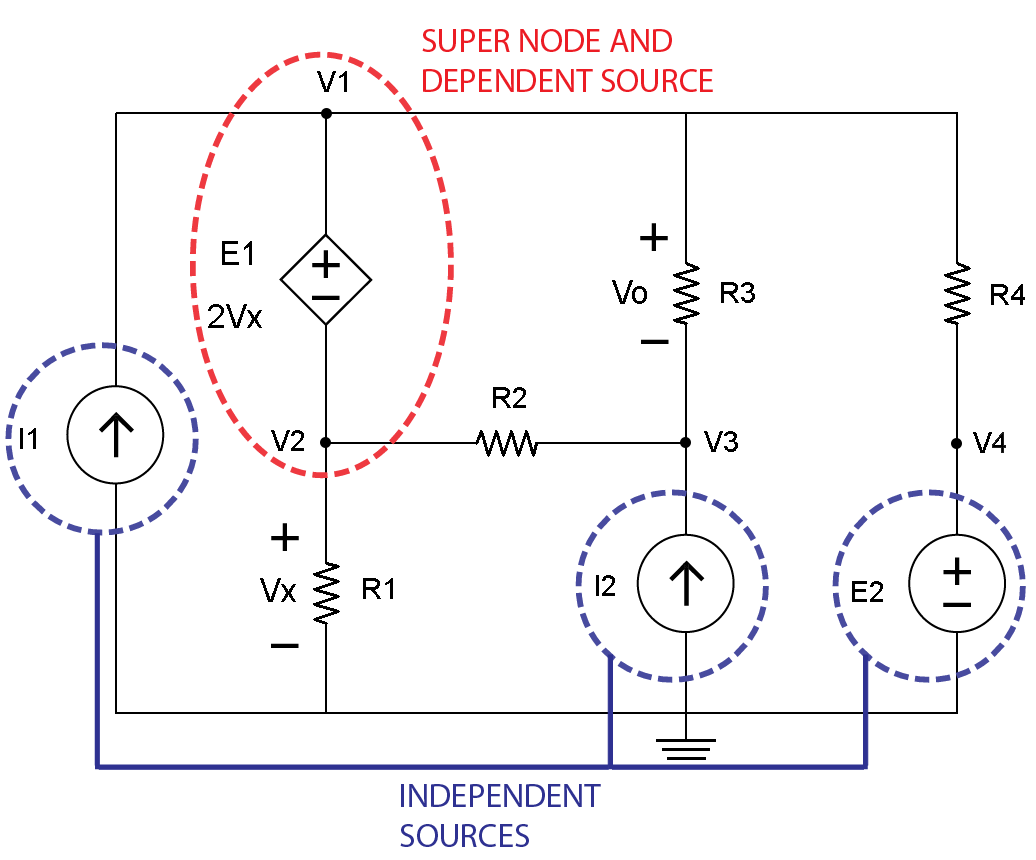
图。 4
第4步是识别超级节点的电流,蓝线和箭头标记为a,b,c,d和e,如图5所示。
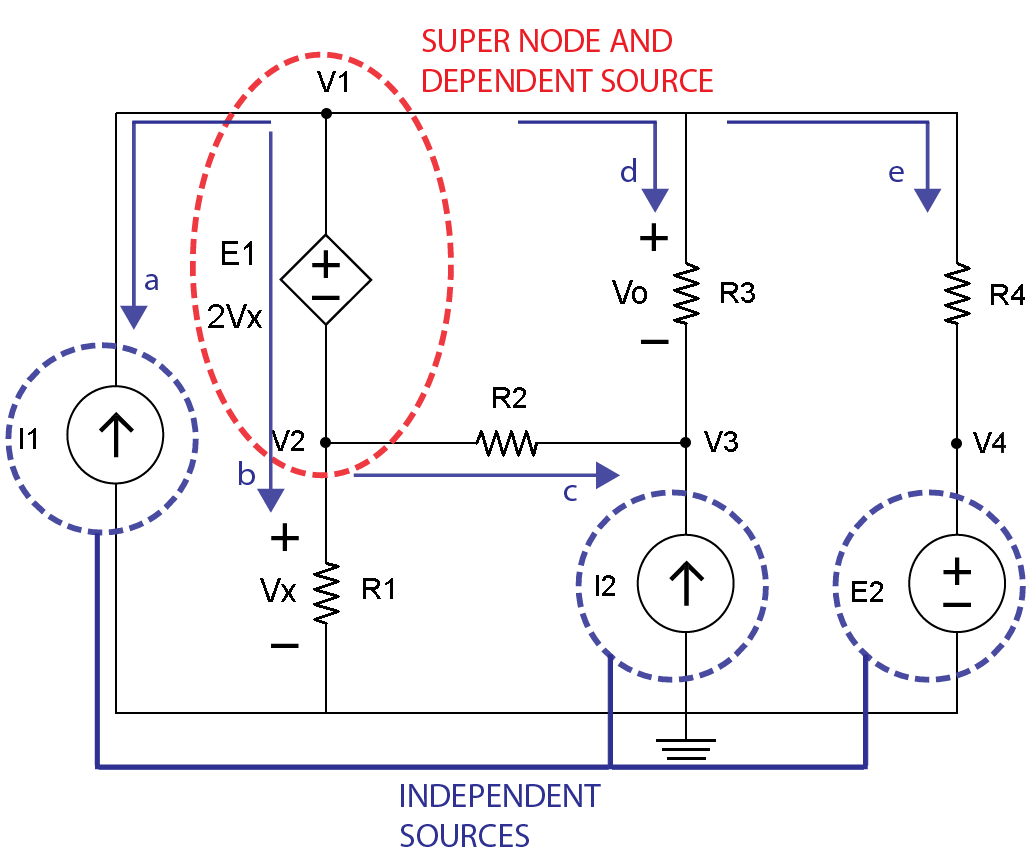
图5
第五步是识别V3节点的电流,红线和箭头标记为f,g和h,如图6所示。
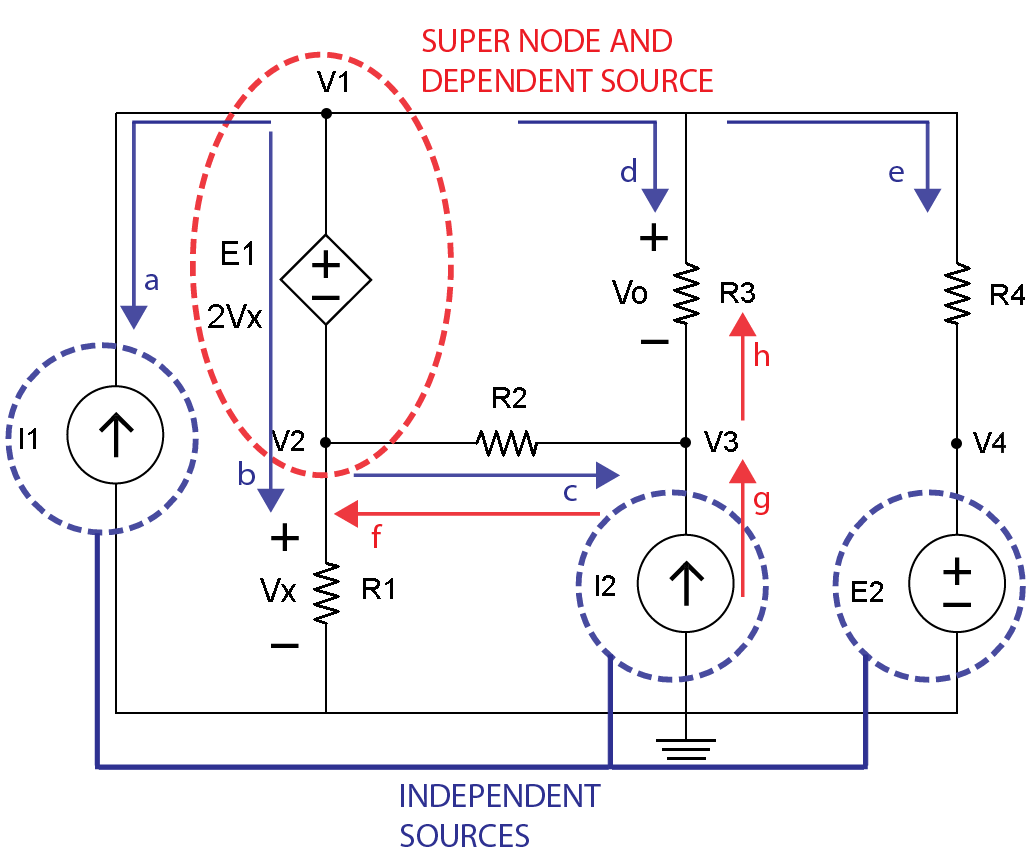
图6
下一步将利用图5标识超级节点,以便识别基尔霍夫电流定律(KCL)方程。请记住,基尔霍夫电流定律(KCL)规定进入和离开节点的所有电流的代数和必须等于零。
以下KCL电流方程可以写入超级节点的蓝线和箭头a,b,c,d和e:
$$ -I_ {1} + I_ {b} + I_ {c} + I_ {d} + I_ {e} = 0 $$
请注意:
$$ I_ {b} = \ frac {V_ {2}} {R_ {1}},I_ {c} = \ frac {V_ {2} - V_ {3}} {R_ {2}},I_ {d} = \ frac {V_ {1} -V_ {3}} {R_ {3}},I_ {e} = \ frac {V_ {1} - E_ {2}} {R_ {4}} $$
现在,等式变为:
$$ -I_ {1} + \ frac {V_ {2}} {R_ {1}} + \ frac {V_ {2} -V_ {3}} {R_ {2}} + \ frac {V_ {1} -V_ {3}} {R_ {3}} + \ frac {V_ { 1} -E_ {2}} {R_ {4}} = 0 $$
替换电路值:
$$ - (\ text {2 m})+ \ frac {V_ {2}} {\ text {1 k}} + \ frac {V_ {2} -V_ {3}} {\ text {2k}} + \ frac {V_ {1} -V_ {3}} { \ text {3k}} + \ frac {V_ {1} -E_ {2}} {\ text {4k}} = 0 $$
将两边乘以12 k(Least CommonDenominator):
$$ [ - (\ text {2 m})+ \ frac {V_ {2}} {\ text {1 k}} + \ frac {V_ {2} -V_ {3}} { \ text {2k}} + \ frac {V_ {1} -V_ {3}} {\ text {3k}} + \ frac {V_ { 1} -E_ {2}} {\ text {4k}} = 0](\ text {12 k})$$
展开:
$$ - 24 + 12V_ {2} + 6(V_ {2} - V_ {3})+ 4(V_ {1} - V_ {3})+ 3(V_ {1} - 4)= 0 $$
$$ - 24 + 12V_ {2} + 6V_ {2} - 6V_ {3} + 4V_ {1} - 4 V_ {3} + 3V_ {1} - 12 = 0 $$
合并条款:
$$ 7V_ {1} + 18V_ {2} - 10V_ {3} = 36 $$ [等式1]
下一步将利用图6显示V3节点处的电流可以为f,g和h的红线和箭头写出方程式。请注意,当查看c和g以及d和h的蓝色和红色线和箭头时,通过电阻器R2和R3的电流方向是相反的。这在检查结果后会很重要。
$$ -I_ {2} + \ frac {V_ {3} - V_ {2}} {R_ {2}} + \ frac {V_ { 3} -V_ {1}} {R_ {3}} = 0 $$
替换电路值:
$$ - (\ text {2 m})+ \ frac {V_ {3} - V_ {2}} {\ text {2 k}} + \ frac {V_ {3} -V_ {1}} {\ text {3 k}} = 0 $$
将两边乘以6 k(最小公分母):
$$ [ - (\ text {2 m})+ \ frac {V_ {3} - V_ {2}} {\ text {2 k}} + \ frac {V_ {3} -V_ {1}} {\ text {3 k}} = 0](\ text {6 k})$$
展开:
$$ - 12 + 3(V_ {3} - V_ {2})+ 2(V_ {3} - V_ {1})= 0 $$
$$ - 12 + 3V_ {3} - 3V_ {2} + 2V_ {3} - 2V_ {1} = 0 $$
组合术语:
$$ - 2V_ {1} - 3V_ {2} + 5V_ {3} = 12 $$ [等式2]
有两个方程和三个未知数。需要另一个等式。当查看图5中有关直流电压源E1和节点V2的给定信息以及电阻器R1上的电压Vx时,可以得到另一个等式。
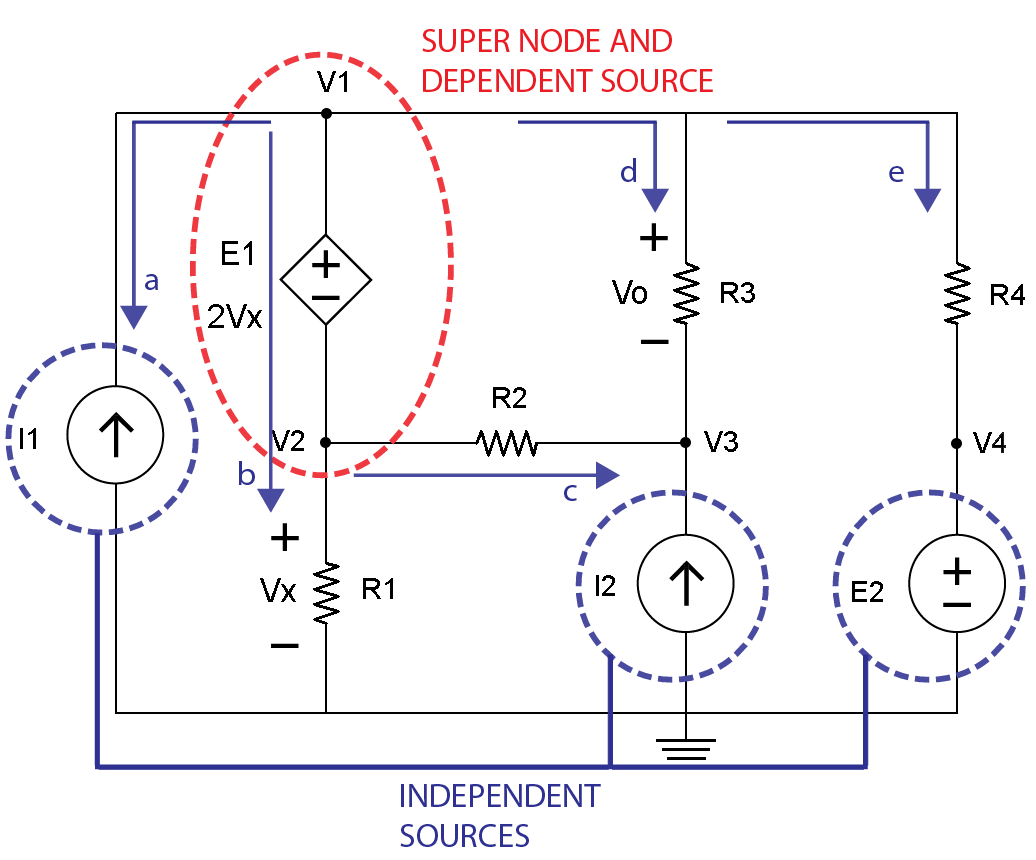
图。 5
以下信息是已知的:
$$ E_ {1} = V_ {1} - V_ {2} $$
$$ E_ { 1} = 2V_ {X} $$
$$ V_ {1} - V_ {2} = 2V_ {X} $$ [等式A]
$$ V_ {2 } = V_ {X} $$ [公式B]
在公式A中使用公式B,其中V2 = Vx,可以得到V1的另一个公式:
$$ V_ {1 } - V_ {2} = 2V_ {X} $$
$$ V_ {1} - V_ {X} = 2V_ {X} $$
解决V1:
$$ V_ {1} = 2V_ {X} + V_ {X} $$
$$ V_ {1} = 3V_ {X} $$ [等式3]
现在,使用公式A和公式B,公式1和公式2需要以Vx和V3表示V1和V2项:
召回等式1:$$ 7V_ {1} + 18V_ {2} - 10V_ {3} = 36 $$
$$ 7(3V_ {X})+ 18(V_ {X}) - 10V_ {3} = 36 $$
$$ 21V_ {X} + 18V_ {X} - 10V_ {3} = 36 $$
$$ 39V_ {X} - 10V_ {3} = 36 $$ [等式C]
召回等式2:$$ - 2V_ {1} - 3V_ {2} + 5V_ {3} = 12 $ $
$$ - 2(3V_ {X}) - 3(V_ {X})+ 5V_ {3} = 12 $$
$$ - 6V_ {X} - 3V_ {X} + 5V_ {3} = 12 $$
$$ - 9V_ {X} + 5V_ {3} = 12 $$ [等式D]
现在有两个方程和两个可以求解的未知数。
$$ 39V_ {X} - 10V_ {3} = 36 $$ [方程C]
$$ - 9V_ {X} + 5V_ {3} = 12 $$ [等式D]
当在等式D的两侧乘以2时,两个等式可以加在一起,导致V3项被取消,留下一个等式为一个未知。
将公式D的两边乘以2:
$$( - 9V_ {X} + 5V_ {3} = 12)(2) $$
展开:
$$ - 18V_ {X} + 10V_ {3} = 24 $$ [公式D]
将新的公式D添加到公式C:
$$ 39V_ {X} - 10V_ {3} = 36 $$ [公式C]
$$ - 18V_ {X } + 10V_ { 3} = 24 $$ [公式D]
$$ 21V_ {X} = 60 $$
解决Vx:
$$ \ underline { V_ {X} = 2.86 \ text {v}} $$
召回:$$ V_ {2} = V_ {X} $$,替换$$ V_ {X} = 2.86 \ text {伏特} $$
$$ \ underline {V_ {2} = 2.86 \ text {v}} $$
召回:$$ V_ {1} = 3V_ {X} $$,替换$$ V_ {X} = 2.86 \ text {volts} $$
$ $ V_ {1} = 3(2.86 \ text {v})$$
$$ \ underline {V_ {1} = 8.58 \ text {v}} $$
当使用公式1和V1和V2的计算值时,可以计算V3:
召回:$$ 7V_ {1} + 18V_ {2} - 10V_ {3} = 36 $$
替换V1和V2的值:
$$ 7(8.58)+ 18(2.86) - 10V_ {3} = 36 $$
展开:
$$60.06 + 51.48 - 10V_ {3} = 36 $$
结合条款:
$$ 111.54 - 10V_ {3} = 36 $$
解决V3:
$$ - 10V_ {3} = -111.54 + 36 $$
将双方除以-10:
$$ \ underline {V_ {3} = 7.55 \ text {v}} $$
可以使用图5计算V0的值:
召回:$$ V_ {0} = V_ {1} - V_ {3} $$
替换V1和V3的值:
$$ V_ {0} = 8.58 \ text {v} - 7.55 \ text {v} $$
$$ \ underline {V_ {0} = 1.03 \ text {v}} $$
既然已知所有节点电压,可以计算电阻器R1(IR1),R2(IR2),R3(IR3)和电阻器的电流R4(IR4)。
召回:$$ I_ {R_ {1}} = \ frac {V_ {2}} {R_ {1}} $$
$$ I_ {R_ {1}} = \ frac {2.86 \ text {v}} {\ text {1 k} \ Omega} $$
$$ \ underline {I_ {R_ {1}} = 2.86 \ text {mA}} $$
召回:$$ I_ {R_ {2}} = \ frac {V_ {2} - V_ {3}} {R_ { 2}} $$
$$ I_ {R_ {2}} = \ frac {2.86 \ text {v} - 7.55 \ text {v}} {\ text {2k} \ Omega} $$
$$ \ underline {I_ {R_ {2}} = -4.69 \ text {v}} $$
$$ \ underline {I_ {R_ {2}} = -2.35 \ text {mA}} $ $
召回:$$ I_ {R_ {3}} = \ frac {V_ {1} - V_ {3}} {R_ {3}} $$
$$ I_ {R_ {3}} = \ frac {8.58 \ text {v} - 7.55 \ text {v}} {\ text {3 k} \ Omega} $$
$$ I_ {R_ {3}} = \ frac {1.03 \ text {v}} {\ text {3 k} \ Omega} $$
$$ \ underline {I_ {R_ {3 }} = 0.34 \ text {mA}} $$
召回:$$ I_ {R_ {4}} = \ frac {V_ {1} - V_ {4} } {R_ {4}} $$
$$ I_ {R_ {4}} = \ frac {8.58 \ text {v} - 4 \ text {v}} {\ text {4 k} \ Omega} $$
$$ I_ {R_ {4}} = \ frac {4.58 \ text {v}} {\ text {4 k} \ Omega} $$
$$ \ underline {I_ {R_ {4}} = 1.15 \ text {mA}} $$
要确认KCL当前计算,请考虑超级节点上关联的那些:
$$ - I_ {1} + I_ {R_ {1}} + I_ {R_ {2}} + I_ {R_ {3}} + I_ {R_ {4}} = 0 $$
替代电路值:
$$( - 2 \ text {mA})+ 2.86 \ text {mA} - 2.35 \ text {mA} + 0.34 \ text {mA} + 1.15 \ text {mA } = 0 $$
结合条款:
$$ 4.35 \ text {mA} - 4.35 \ text {mA} = 0 $$
确认V3节点的KCL当前计算:
$$ - I_ {2} + I_ {R_ {2}} + I_ {R_ {3}} = 0 $$
注意IR2和IR3是超级节点计算的相反符号
$$( - 2 \ text {mA})+ 2.35 \ text {mA} - 0.34 \ text {mA} = 0 $$
组合术语:
$$ (-2.34 \ text {mA})+ 2.35 \ text {mA} \ approx0 $$
电压控制电流源是输出电流(IS)是线性的具有以下关系中的参考电压(VX)的连通组件的功能:
IS =(A)(IX)其中A是乘数,需要确定IX。
VCCS的下图如图1所示。
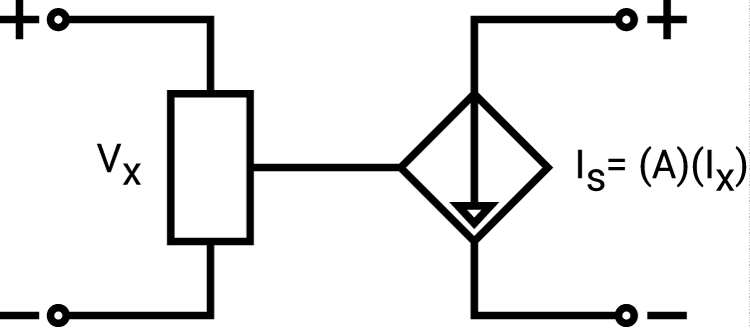
图1.压控电流源
考虑以下电路,该电路由依赖电压源I2组成值(-2mA)(VR1),与电阻R1的连接链路,其值为1K欧姆,电压降为VR1,独立电压源V1的值为4伏,独立电流源I1具有值1 mAmp,如图2所示。
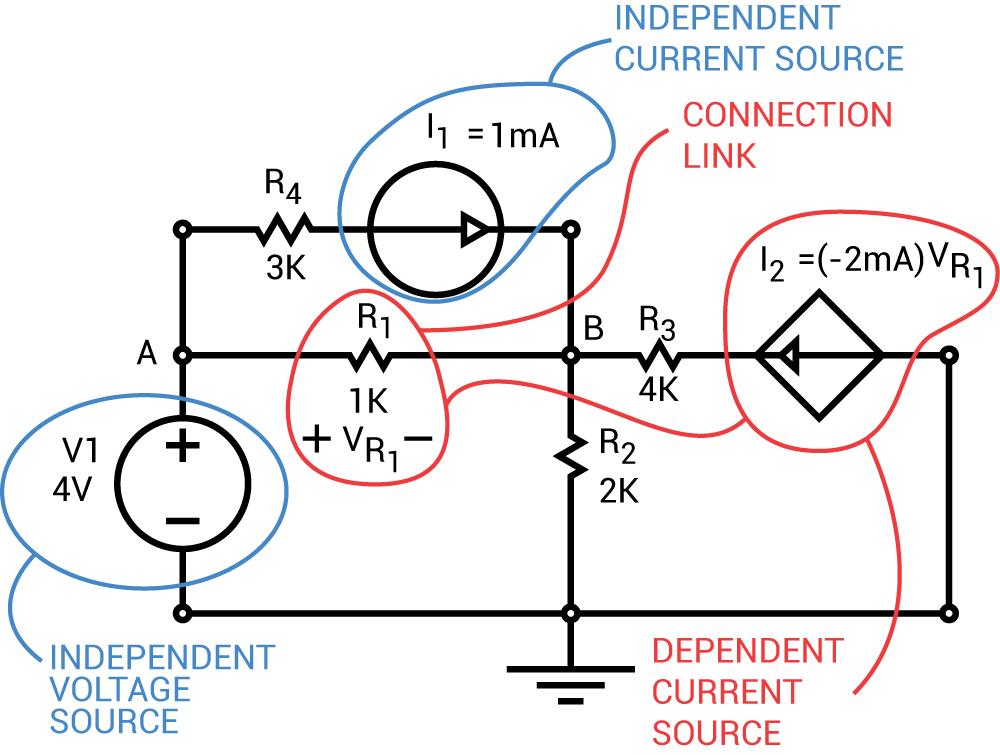
图2。
在节点B使用基尔霍夫电流定律(KCL)之前,节点A的电压可以使用4伏的独立电压源V1的值来确定:
$$ V_ {A} = V_ {1} = 4 \ text {volts} $$
要确定节点A处的KCL,需要识别电流。电流IA是正的,因为它进入节点而电流IB和IC是负的,因为它们离开节点,如图3所示。

图3.
节点VA上所有电流的代数和等于零:
$$ I_ {A} - I_ {B} - I_ {C} = 0 $$
请注意:
$$ I_ {B} = \ frac {V_ {B} - V_ {A}} { R_ {1}} $$
$$ I_ {C} = I_ {1} $$
这样:
$$ I_ {A} - \ frac {V_ {B} - V_ {A}} {R_ {1}} - I_ {1} = 0 $$
替换电路值:
$$ I_ {A} - \ frac {V_ {B} - 4} {1 \ text {k} \ Omega} - 1 \ text {mA} = 0 $$
将两边乘以1k:
$$ [I_ {A} - \ frac {(V_ {B} - 4)} {1 \ text {k} \ Omega} - 1 \ text {mA} = 0](1 \ text {k} )$$
展开:
$$(1 \ text {k})I_ {A} - (V_ {B} - 4) - 1 = 0 $$
$$(1 \ text {k})I_ {A} - V_ {B} + 4- 1 = 0 $$
组合术语:
$ $(1 \ text {k})I_ {A} - V_ {B} + 3 = 0 $$
左侧未知,右侧知道
$$(1 \ text {k})I_ {A} - V_ {B} = -3 $$ [等式1]
要确定节点B处的KCL,需要识别电流。当前的IA,IB和IC是正的,因为它们进入节点,而当前的IE是负的,因为它离开节点,如图4所示。

图4.
节点VB上所有电流的代数和等于零:
$$ I_ {B } + I_ {C} + I_ {D} - I_ {E} = 0 $$
请注意:
$$ I_ {B} = \ frac {V_ {A } -V_ {B}} {R_ {1}} $$
$$ I_ {C} = I_ {1} $$
$$ I_ {D} = I_ {2} $$
$$ I_ {E} = \ frac {V_ {B}} {R_ {2}}
这样:
$$ \ frac {V_ {A} -V_ {B}} {R_ {1}} + I_ {1} + I_ {2} - \ frac {V_ {B}} {R_ {2}} = 0 $$
替换电路值:
$$ \ frac {4-V_ {B}} {1 \ text {k} \ Omega} + 1 \ text {mA} - (2 \ text {m})V_ {R_ {1}} - \ frac {V_ {B}} {2 \ text {k} \ Omega} = 0 $$
将两边乘以2 k:
$$ [\ frac {4-V_ {B}} {1 \ text {k} \ Omega} + 1 \ text {mA} - (2 \ text {m})V_ {R_ { 1}} - \ frac {V_ {B}} {2 \ text {k} \ Omega} = 0](2 \ text {k})$$
展开:
$$ 2(4 -V_ {B})+ 2 -4V_ {R_ {1}} -V_ {B} = 0 $$
$$ 8 -2V_ {B} + 2 -4V_ {R_ {1}} -V_ {B} = 0 $$
组合术语:
$$ - 3V_ {B} -4V_ {R_ {1}} + 10 = 0 $$
左边未知,右边知道
$$ - 3V_ {B} -4V_ {R_ {1}} = -10 $$ [等式2]
$$ E_ {R_ {4}} = I_ {1} R_ {4} $$
替换电路值:
$$ E_ {R_ {4}} =(1 \ text {mA})(3 \ text {k} \ Omega)$$
$$ \ underline {E_ {R_ {4}} = 3 \ text {v}} $$
请注意,R4与R1并行。这使得ER4等于VR1。
$$ \ underline {V_ {R_ {1}} = 3 \ text {v}} $$
使用欧姆定律找到IB:
\ [I_ {B} = \ frac {V_ {R1}} {R_ {1}} \]
替换电路值:
$$ I_ {B} = \ frac {3 \ text {v}} {1 \ text {k} \ Omega} $$
$$ \ underline {I_ {B} = 3 \ text {mA}} $$
回忆节点A的电流:
$$ I_ {A} -I_ {B} -I_ {C} = 0 $$
求解IA:
$$ I_ {A} = I_ {B} + I_ {C} $$
替代电路值:
$$ I_ {A} =(3 \ text {mA})+(1 \ text {mA})$$
$$ \ underline {I_ {A} = 4 \ text { mA}} $$
请注意,当前ID是当前的I2:
$$ I_ {D} =( - 2 \ text {m}) (V_ {R_ {1}})$$
替换电路值:
$$ I_ {D} =( - 2 \ text {m})(3 \ text { v})$$
$$ \ underline {I_ {D} = - 6 \ text {mA}} $$
回忆节点电流B:
$$ I_ {B} + I_ {C} + I_ {D} -I_ {E} = 0 $$
解决IE:
$$ I_ {E} = I_ {B} + I_ {C} + I_ {D} $$
替换电路值:
$$ I_ {E} = (3 \ text {mA})+(1 \ text {mA})+( - 6 \ text {mA})$$
$$ \ underline {I_ {E} = - 2 \ text {mA}} $$
请注意,VR1可以从节点A和节点B确定:
$$ V_ {R_ {1}} = V_ {A} -V_ {B} $$
解决VB:
$$ V_ {B} = V_ {A} -V_ {R_ {1}} $$
替换电路值:
$$ V_ {B} =(4 \ text {v}) - (3 \ text {v})$$
$$ \下划线{V_ {B} = 1 {\ text {v}}} $$
使用与从属电流源关联的等式来查找当前的I2:
$$ I_ {2} =( - 2 \ tex t {m})(V_ {R_ {1}})$$
替换电路值:
$$ I_ {2} =( - 2 \ text {m})(3 \ text {v})$$
$$ \下划线{I_ {2} = - 6 \ text {mA}} $$
使用欧姆定律查找电阻R3上的电压:
$ $ E_ {R_ {3}} =(I_ {2})(R_ {3})$$
替换电路值:
$$ E_ {R_ {3}} =( - 6 \ text {mA})(4 \ text {k} \ Omega)$$
$$ \ underline {E_ {R_ {3}} = - 24 \ text {v}} $$
为了确认涉及独立电压源V1和电阻器R1和R2的KVL回路,得到以下等式:
$$ V_ {1} = E_ {R_ {1}} + E_ {R_ {2}} $$
替换电路值并注意ER2等于VB
$$(4 \ text {v}) =(3 \ text {v})+(1 \ text {v})$$
使用依赖源的节点分析利用Kirchhoff的当代法与代数和欧姆定律来代替节点的未知电压并找到其他电路值。通过花时间仔细标记节点,通过识别正确的节点电压和极性,解决问题变得更容易并且可以避免错误。
- 相关推荐
- 热点推荐
- 节点分析技术
-
节点电压法中电压源的处理方法2024-08-06 4595
-
节点电压法中电压源怎么处理2024-07-12 7255
-
电路分析技术之节点电压分析2022-11-15 4740
-
【科普视频】你知道电压源和电流源的区别吗?2022-01-12 1527
-
设计过程中如何使用节点分析的交流稳态值2020-12-09 2820
-
节点电压分析2020-10-05 3501
-
节点电压分析电路2019-06-23 11117
-
电路节点分析2018-10-17 2844
-
基于节点依赖度的社团结构发现算法2017-11-20 1169
-
电路分析网孔分析和节点分析2017-03-14 2271
全部0条评论

快来发表一下你的评论吧 !

