

执行节点分析时的特殊情况介绍
描述
当我们在设计电子电路时,了解流过元件的电流量或电路中特定节点在其工作的关键点存在多少电压始终是很重要的。使用基尔霍夫电路定律可以完成任一测量。允许我们找到这些值的两种分析类型是网格分析和节点分析。如果我们试图在一个点(节点)找到电压,那么我们可以使用基尔霍夫电流定律(KCL)进行节点分析。
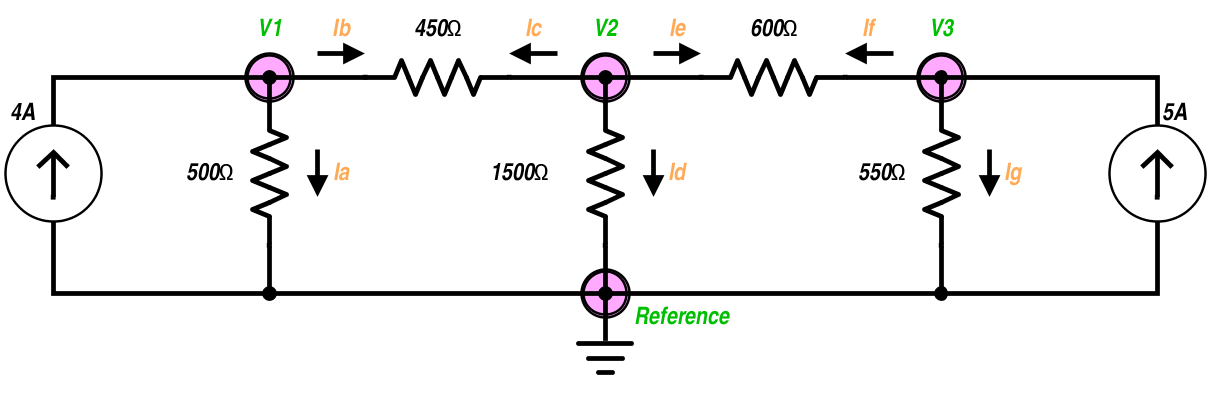
此原理图中的每个特定节点(V1,V2和V3)都有3个连接。 KCL声明每个节点的所有分支电流之和为零。我们可以用它来通过以下方法找到每个节点的电压:
首先,我们有一个具有最低电位的参考节点,称为地。选择该电路中的地是因为它是具有最低电压的共同点。接下来,我们为每个电压未知的节点分配一个变量。这由V1,V2和V3处的圆圈标记。第三,应用KCL形成每个未知电压的等式。
对于节点V1:
电流Ia和Ib :
$$ Ia $$ = $$ \ frac {V1} {500Ω} $$和$$ Ib = \ frac {(V1-V2)} {450Ω} $$
这是因为通过电阻器的电压是两个节点之间的电位差。由于V1是唯一直接连接到4安培电流源的节点,因此$$ Ia + Ib = 4安培$$。
将所有这些放在一起:
$$ \ frac { V1} {500Ω} + \ frac {(V1-V2)} {450Ω} = 4安培$$。
这可以改写为:
$$ V1(\ frac) {1} {500Ω} + \ frac {1} {450Ω}) - V2(\ frac {1} {450Ω})= 4安培$$。
对于节点V2:
Ic从V2指向V1,因此我们将450Ω电阻分支写为:$$ \ frac {(V2-V1)} {450Ω} $$。
Id简单地说:$$ \ frac {V2} {1500Ω} $$。
即从V2流向V3并记为:$$ \ frac {(V2-V3)} {600Ω} $$。
请记住,KCL要求所有3个分支的总和为零。这意味着$$ Ic + Id + Ie = 0 $$。
作为一个公式,它被组合为:
$$ \ frac {(V2-V1)} { 450Ω} + \ frac {V2} {1500Ω} + \ frac {(V2-V3)} {600Ω} = 0 $$。
线性方程的一个更友好的形式是:
$$ - V1(\压裂{1} {450})+ V2(\压裂{1} {450} + \压裂{1} {1500} + \压裂{1} {600}) - V3(\ frac {1} {600})= 0 $$。
节点V3与节点V1的结构相同,只有不同的值。
Ig是:$$ \ frac { V3} {550Ω} $$。
如果(eye-eff,而不是iff。英语嘲笑我们!)是:$$ \ frac {(V3-V2)} {600Ω} $$。
两个电阻都来自5安培电流源,使得If If + Ig = 5 A $$。
放在一起,我们有:
$$ \ frac {(V3-V2)} {600Ω} + \ frac {V3} {550Ω} = 5 A $$。
为计算而兴奋,等式为:
$$ - V2(\压裂{1} {600})+ V3(\压裂{1} {550} + \压裂{1} {600})= 5 $$
第四步也是最后一步是解决方程组。有计算器可以解决线性方程组。 Matlab和GNU Octave是可以执行此功能的PC程序。用铅笔,纸和20分钟的时间;我们可以用代数解决这个“老派”。然而,我们不妨使用更快,更可靠的方法,所以让我们选择www.wolframalpha.com的在线选项。
我们的三个最终方程可以组合在一起:
$$ v1(\ frac {1} {500} + \ frac {1} {450} - v2(\ frac {1} {450})= 4 $$,
$$ - v1(\ frac {1} {450})+ v2(\ frac {1} {450} + \ frac {1} {1500} + \ frac {1} {600}) - v3(\ frac {1} { 600})= 0 $$,
$$ - V2(\压裂{1} {600})+ V3(\压裂{1} {550} + \压裂{1} {600}) = 5 $$。
虽然这在数学上是正确的,但WolframAlpha基本上回复了“呵呵”。
为了使公式更加合适,让我们用“*”代替乘法:
$$ v1 *(\ frac {1} {500} + \ frac {1} {450} -v2 *(\ frac {1} {450})= 4 $$,
$$ - v1 *(\ frac {1} {450})+ v2 *(\ frac {1} {450} + \ frac {1} {1500} + \ frac {1} {600 }) - v3 *(\ frac {1} {600})= 0 $$,
$$ - v2 *(\ frac {1} {600})+ v3 *(\ frac {1 } {550} + \ frac {1} {600})= 5 $$。
解决方案有点乱,因为
$$ \ underline {v1 = \ frac { 3159000} {1697}} $$。
但是点击网页上的近似表格e将产生:
$$ \ underline {v1 = 1,861.5} $$,$$ \ underline {v2 = 1,736.9} $$和$$ \ underline {v3 = 2,265.5} $$。
要检查这一点,请将从两个电源流入电路的功率与电阻器消耗的功率进行比较。节点V1具有1,861.5伏特,4安培等于7,446瓦特。在5安培时,电压为2,265.5伏,节点V3的功率为11,327.5瓦。电阻器以下列速率产生热量:450Ω34.5瓦,500Ω6,930.36瓦,1500Ω2011.21瓦,600Ω467.7瓦,550Ω9,331.8瓦。功率为18,773.5瓦。由于四舍五入问题,功耗为18,773.57瓦。要么我们设计了世界上最强大的烤箱,要么我们的电流应该少一点这个例子!
特殊情况:电压源和超级节点。
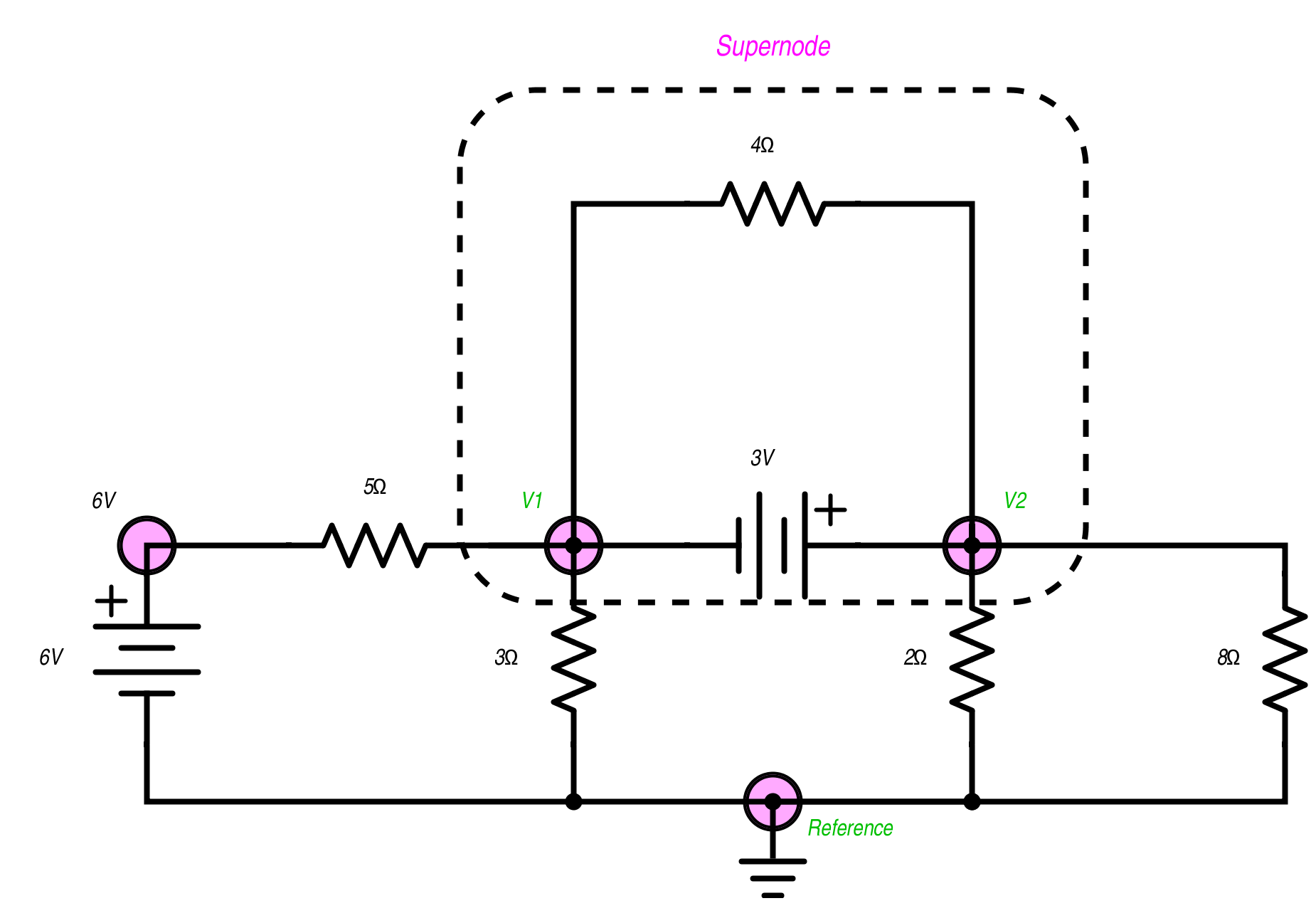
增加电压源是一种特殊情况。这里我们有一个6伏电源和3伏电源。 3伏电源位于两个非参考节点之间,形成一个超级节点。
查找参考节点的过程与上一个例子中的过程相同。
现在情况有所改变位。 6V节点不需要KCL,因为我们已经知道该位置的电路是6伏。超级节点没有它看起来那么糟糕,我们只需要添加一个KVL方程。 3伏电池的V2侧具有比V1侧更高的电压电位,因此我们将使用的KVL是$$ V2-V1 = 3V $$。
其余电路的KCL是:
$$ \ frac {(V1-6v)} {5Ω} + \ frac {V1} {3Ω} + \ frac {V2} {2Ω} + \ frac {V2} {8Ω} = 0 $$。
您可能已经注意到此示例中的数学运算并不那么混乱。我们选择除以阻力而不是乘以倒数。无论哪种方式都是完全有效的。
嘿! 4Ω电阻怎么样?没有人想被排除在外!那么,4Ω电阻是封装协议的一部分。它被视为超级节点的一部分,不必作为单独的等式考虑在内。幸运的是我们!
我们可以在线性方程中添加一些括号,使事情更加清晰,并将它们输入到WolframAlpha页面中:
$$ v2-v1 = 3 $$,$$ \ frac {(v1-6)} {5} + \ frac {(v1)} {3} + \ frac {(v2)} {2} + \ frac {(v2)} {8} = 0 $$。
瞧,我们发现:$$ \ underline {V1 = -0.5827} $$和$$ \ underline {V2 = 2.4173} $$作为我们的答案。
尽管看起来很复杂,节点分析是许多电路仿真程序的基础,也是理解电路中交叉点电压的基石。
-
什么情况下不能用节点电压法2024-08-06 2638
-
回路电流法特殊情况分析处理(2)#电路未来加油dz 2023-09-04
-
电工技术: 节点电压法的特殊情况之一#电工学习电子 2022-11-13
-
#硬声创作季 电路分析与测试:2-4.2特殊情况下节点电压方程的列写方法Mr_haohao 2022-10-28
-
在特殊情况下,封装压电陶瓷可倒置使用2020-09-10 968
-
Dropout如何成为SDR的特殊情况2018-08-15 4398
-
执行机构和定位驱动器介绍2017-10-24 744
-
Zigbee在大数量节点应用中的问题研究2009-05-26 559
全部0条评论

快来发表一下你的评论吧 !

