

RLC串联电路的相量图_RLC串联电路的频率响应
电子说
描述
RLC串联电路的相量图
在相量上,表明各个相量之间的相位关系非常重要,在指定电流的初相角的情况下,可接初相角画出其相量,若在题目中只给定了电流的有效值,而没有给定初相角的情况下,可设电流为参考正弦量,令其初相角为0,其他相量可根据与参考正弦量的关系而做。在串联电路中,以电流I为参考正弦量较方便。如图9-1-3,9-1-4。
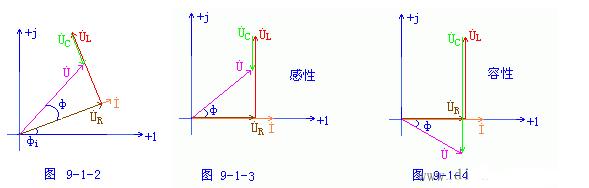
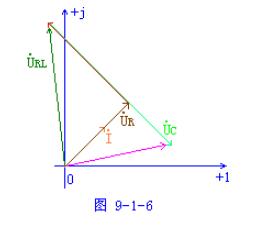
由以上分析可以看出:三个电压的有效值之间形成直角三角形-电压三角形,故若将电压三角形三边分除以I,得到阻抗三角形。如图9-1-5。
从电压三角形可以看出:

【实例9-1】一个实际的电感线圈具有电阻R=30Ω,L=127mh,与电容器C=40μF串联后接至电压 的电源上。如图例9-1。
求:①复阻抗,电流的有效值、相量、瞬时值。②电容和线圈上电压的瞬时值。③作电压、电流相量图。

RLC串联电路的频率响应
研究物理量与频率关系的图形(谐振曲线)可以加深对谐振现象的认识。下面讨论在如图1所示RLC串联电路中的频率响应 。
。
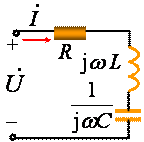
图1 RLC串联电路
根据电路联接关系,得到
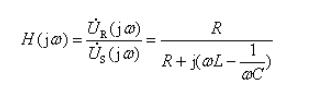
为比较不同回路,令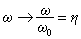 ,则上式改写为
,则上式改写为
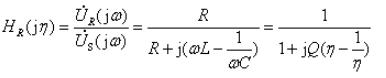
相频特性: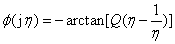
幅频特性:
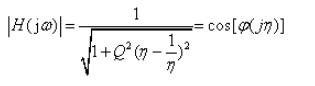
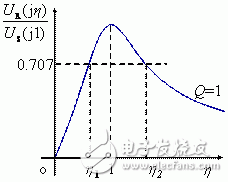
图2所示为不同品质因素Q下,频率响应随η的变换情况。
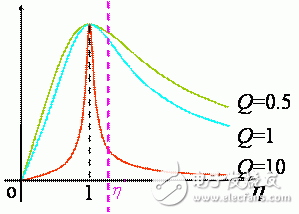
图2 RLC串联电路频率响应曲线
表明:
① 谐振电路具有选择性
在谐振点响应出现峰值,当ω偏离ω0时,输出下降。即串联谐振电路对不同频率信号有不同的响应,对谐振信号最突出(响应最大),而对远离谐振频率的信号具有抑制能力。这种对不同输入信号的选择能力称为“选择性”;
② 谐振电路的选择性与Q成正比
Q越大,谐振曲线越陡。电路对非谐振频率的信号具有强的抑制能力,所以选择性好。因此Q是反映谐振电路性质的一个重要指标;
③ 谐振电路的有效工作频段
将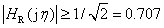 所对应的频域范围称为带宽,如下图所示。其中
所对应的频域范围称为带宽,如下图所示。其中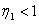 ,称为下限截止频率;
,称为下限截止频率;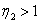 ,称为上限截止频率。通带BW=ω2—ω1。
,称为上限截止频率。通带BW=ω2—ω1。
-
rlc串联谐振电路的主要特点2023-12-14 7666
-
rlc串联谐振电路图和原理2019-05-08 4617
-
串联RLC电路的谐振2019-08-20 4732
-
串联谐振电路图2020-05-19 2705
-
rlc串联谐振电路的频率响应2020-09-04 1820
-
RLC串联谐振电路实验方法2020-09-22 5847
-
rlc串联谐振电路图以及原理详解2007-12-03 24264
-
RLC串联电路谐振特性的Multisim仿真2012-01-31 2602
-
电路设计--RLC串联电路2017-02-28 1156
-
电路的频率响应学习课件免费下载2020-11-03 1304
-
怎么判断RLC串联电路是否达到谐振状态?2023-10-11 7575
-
RLC电路发生串联谐振的条件是什么?有哪些特点?2023-12-20 4443
-
如何判断rlc串联电路达到谐振状态2024-03-09 6173
-
rlc串联谐振电路的主要特点 RLC串联谐振电路图2024-07-17 31580
-
rlc串联谐振电路频率特性的特点2024-07-15 4895
全部0条评论

快来发表一下你的评论吧 !

