S.A.谢昆诺夫及其对波导理论的贡献有多大？

谢昆诺夫（S.A. Schelkunoff）是国际知名的电磁理论科学家。从1934年解决同轴线内电磁场结构开始，他在后来的三十年内，在工程电磁场、天线理论、波导理论等方面发表了数十篇论文和几本书，提出了许多定理、原理、概念、方法（它们之中有许多早已写人大学教材中），作出了重要的贡献。他使应用数学焕发出光采，许多工作带有奠基性质。就经典电动力学方法（即量子理论以外领域）而言，可以把他比作二十世纪的麦克斯韦。众所周知，电磁波的波导在微波技术中有广泛应用，也是当前光波导光纤的前驱，因而介绍这方面的历史是有意义的。

一

1897年1月27日，谢昆诺夫生于俄国萨马拉，后随家庭移居美国。1923年（26岁时）在华盛顿州立学院获硕士学位后，即加人西屋公司工作，两年后转人贝尔研究所。1928年，他在哥伦比亚大学获博士学位。以后，长期在贝尔研究所担任高级科学家。

谢昆诺夫开始从事研究工作的时期，正处在电子学从短波技术向超高频、微波技术发展的时代。笔者在前文[1]中，曾谈过两位英国物理学家（O. Heaviside和J.J. Thomson）于1893年就波导的可实现性发表尖锐对立的意见的情形。显然，只有实验上的完全成功，才能对这一争论的是非作出最后的判断。在贝尔研究所，一方面有以G.C. Southworth为首的小组从事建立波导线路的实验研究，同时又有以J.R. Carson为首的小组进行波导理论的数学分析工作。谢昆诺夫参加了后者。1936年，Carson，Mead和谢昆诺夫发表了题为《高频波导数学理论》的论文，该论文反映的最重要的成果是导出了圆波导的严格的超越方程（即CMS方程[2，3]）。论文中假定壁电导率为有限，同时作混合模（hybrid modes）分析。论文所导出的CMS方程实质是本征值方程，具有重要意义和实用价值。正是这篇论文命名了HE和EH模。CMS方程是针对金属壁波导提出的，但经过J.A. Stratton[4]的普遍化讨论后，也适用于近代出现的光纤。因此，正是从1936年开始，谢昆诺夫和比他年长的贝尔研究所的研究数学家（research mathematician）J.R. Carson一起，作出了极有价值的贡献。实际上，1934年谢昆诺夫在独立发表关于同轴线这一双导体导波体系的理论时[5]，就一直在思考如何从数学上来处理单导体导波体系的波导问题。

1937年，谢昆诺夫发表了题为《平面电磁波传输理论》的论文[6]，单独一人作出了非常重要的贡献。在这篇论文中，他率先把阻抗概念用于处理电磁场问题；他提出了无耗波导截止频率的定义；他首创计算衰减常数的功率损耗法（power loss method），这在V.M. Papadopoulos[7] 1954年论文发表之前是唯一能作数值计算的方法；他最先采用分布参数等效电路以分析自由空间的和导波的传播，在这过程中，他利用矢量势（vector potential）A作为工具。实际上，他的这些研究成果早已成为电磁场理论、波导理论教科书的基本内容。

三十年代末至五十年代初，是谢昆诺夫的多产时期，其间屡有佳作。例如，1938年他研究了微小失圆管子中的导波[8]；1944年他对无限长矩形波导中的TE10（H10）模的纯行波，定义了一组（三个）特性阻抗[9]；1952年他提出“广义电报员方程”[10]，这是研究圆波导中TE01（H01）模传输的有力工具，在1955年以后人们用它解决了许多问题（实际上，正是谢昆诺夫最先指出圆波导中存在频率越高衰减越小的模式，即H01模）。这些都是对波导理论直接作出的贡献。同波导理论间接有关的工作也很多，例如，1948年他讨论了由均匀媒质等效空间网络导出麦克斯韦方程组[11]；1951年提出电磁场等价定理（field equivalence theorems）[12]，它可用来解决波导的小孔激发理论问题；1952年，他由半无限导体圆锥的分析，解决了半无限长线电流产生的场分布[13]；1955年，他通过正交函数展开，将麦克斯韦方程组转换为具体问题的耦合波方程组[14]等等。

二

指出下述的年代方面的巧合是非常有趣的：谢昆诺夫出生的那一年（1897），恰恰是瑞利第一次全面讨论波导的那年[15,16]，从那时到波导实验成功（1936）[17]恰为39年；而谢昆诺夫正是在39岁时，参加Carson领导的小组完成了对圆波导特征方程的推导工作[2]。

基于一种科学思维上的敏感或直觉，谢昆诺夫对平面电磁波（一种非常基本的波）的性质进行了深人的研究。他指出[6]，平面波可在理想导电壁金属管子（图1）中存在，但是近似平面的，等相面在边界上畸变。

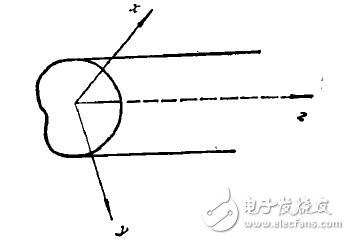
图1、任意截面规则波导

从单色简谐波条件下的麦克斯韦方程出发，在横磁（TM）波和Hz=0的假定下，可以写出标量Ex，Ey，Ez，和Hx，Hy，Hz之间的关系式；又假定某个电位函数U（表示在给定点与无限远之间沿着等相面上一条路径的电动势作用），从而写出

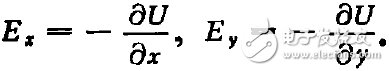
此外，引入矢量势函数A（它的旋度是磁场强度矢量H），取A为z向矢量（A=Aziz，iz为z向单位矢），则得

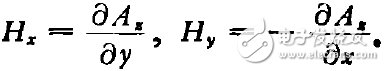
联立以上三方面的关系式，可得

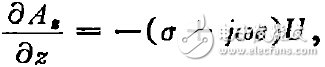
    （1）

式中σ，是波导内填充介质的电导率和介电常数。把上式与均匀传输线方程比较，可得取

   （2）

作为横磁波传输等效为分布参数电路时的并联导纳.这样，谢昆诺夫开始在用等效电路描述波动过程方面取得突破。

由麦克斯韦方程及上述关系式，可得

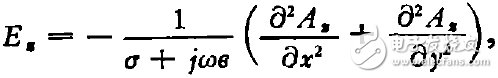
    （3）

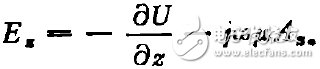
    （4）

把（1）式代入（4）式，得

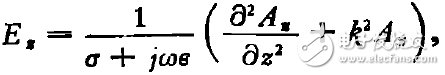
    （5）

式中

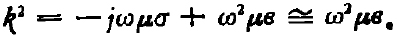
对比（3），（5）两式，得

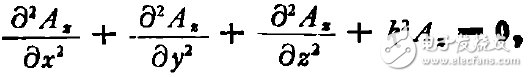
即

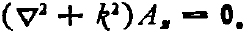    （6）

这是无源空间的齐次Helmholtz方程，说明Az（或说矢量A）是波方程的解。令

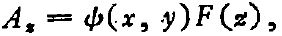
式中函数ψ表示场振幅在等相面上的分布；代入（5）式，得

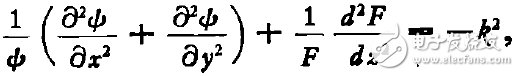
式中左边第一项与z无关，可令

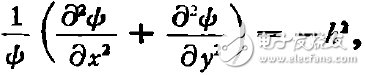
式中h与（x，y，z）及ψ无关。由于ψ是实数，故h也是实数。又因F(z)与（x，y）无关，故可取

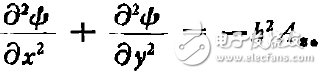
    （7）

将（7）式带入（3）式后，得

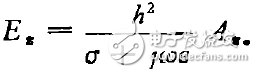
    （8）

将（8）式与（4）式联立，得

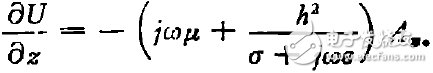
    （9）

对比均匀传输线理论中的公式：

可取

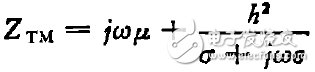
    （10）

作为横磁波传输分布等效电路的串联阻抗，现在可用图2来描写TM波的波动过程，并由（2）式和（10）式来决定元件的值：

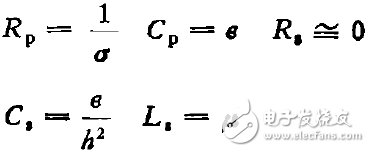
    （11）

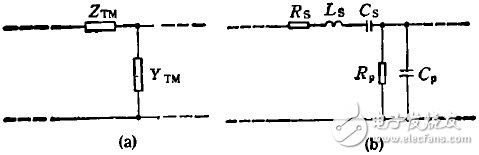
图2、规则柱波导的TM波等效电路

当然，参照滤波器理论还可求传播常数、特性阻抗和截止频率的表达式。

谢昆诺夫的上述处理不仅在理论上优美、自洽，而且在工程计算上很方便。例如，对于圆波导和TM01模，有

    （12）

式中k01为Bessel函数J0（x）=0的第一根，a为波导内半径。

三

波导实验成功后最初几年，人们吃不准该怎样看待它。问题是能否把它看成传输线？能否计算它的阻抗和反射？正是谢昆诺夫及时解决了这些问题。1937年，他首先提出了波导的波阻抗的定义。1944年，他又提出了特性阻抗的定义。他的分析主要针对矩形波导（图3）。

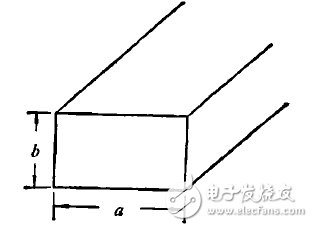
图3、矩形波导

其中的横向电场与横向磁场的关系，对TE模为：

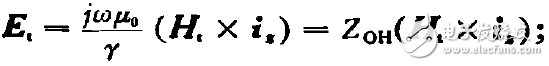
    （13）

对理想导电壁波导主模（H10模），可证明

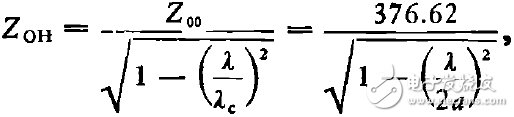
    （14）

式中λ是工作波长，λc是截止波长，Z00是自由空间波阻抗。波导波阻抗是有用的概念，但却无法解释两段波导（a一样，b不同）相联后有反射发生的事实。

三十年代末到四十年代初的微波测量实践，证明关于行波、驻波、反射、圆图等传输线概念、方法均可用于波导。因而为了应用传输线理论就必须在单导体的波导情况下给出电压和电流的定义。谢昆诺夫最早做了这个工作[9]。对矩形波导主模，他定义

    （15）

    （16）

这样他导出了一组（三个）特性阻抗：

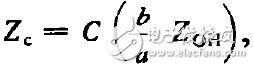
    （17）

式中常数C可以是π|2，2，π2|8，因而特性阻抗失去了唯一性。由于表达式包含了b，因而解决了矛盾。

这是一个贡献，但谢昆诺夫自己也认为这种处理不太自然。对这个问题，几十年来发生许多争论[18-20]，我们认为D.M Kerns[19]的见解比较正确、全面；他认为，由线积分定义电压没有普遍价值，因为并非在一切情况下均能知道波导内的场图。其次，“ 一根波导的特性阻抗”的说法没有意义，因为波导内有多模，每个模式都有自己的波阻抗值。但Kerns并不完全否定谢昆诺夫的方法在分析波导中不连续性问题时有价值，因而与完全否定的观点[20]不同。

目前采用的定义波导电压和电流的方法是以基准场（basis fields）理论为基础。这一较好方法是S.Silver[21]最先提出的。它把波导内横向场写为

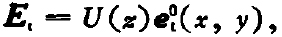    （18）

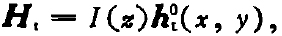    （19）

Silver把式中的U，I分别称为模式电压、电流参数。今天，我们称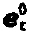为基准电场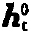，为基准磁场。上述不用线积分定义电压的方式比谢昆诺夫无疑前进了一步。

但是，谢昆诺夫的方法直到今天仍在使用着。例如，1983年发表的关于双脊波导的论文山[22]，对电压的定义为

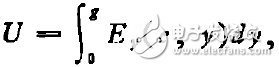
这显然仍是谢昆诺夫方式。因此，向人们介绍这位在本世纪三十至六十年代非常活跃的电磁理论科学家的成就是十分必要的。

本文只是简介谢昆诺夫在波导理论研究早期所做工作，绝非其贡献的全部。但就本文内容已经可以看出，他的主要特点是理论思维方面的创新精神。虽然他毕生未做实验工作，但令人惊奇的是他对事物总保持高度敏感并且总能在数学上找到处理的方法。

参考文献：

作者：黄志询，北京广播学院微波工程系