五款经典运放电路分享

　　1、反向放大器电路

　　运放的同向端接地=0V，反向端和同向端虚短，所以也是0V，反向输入端输入电阻很高，虚断，几乎没有电流注入和流出，那么R1和R2相当于是串联的，流过一个串联电路中的每一只组件的电流是相同的，即流过R1的电流和流过R2的电流是相同的。

　　

　　流过R1的电流：

　　I1=（Vi-V-）/R1……a

　　流过R2的电流：

　　I2=（V—Vout）/R2……b

　　V-=V+=0……c

　　I1=I2……d

　　求解上面的初中代数方程，得：

　　Vout=（-R2/R1）*Vi

　　这就是传说中的反向放大器的输入输出关系式了。

　　2、减法器电路

　　

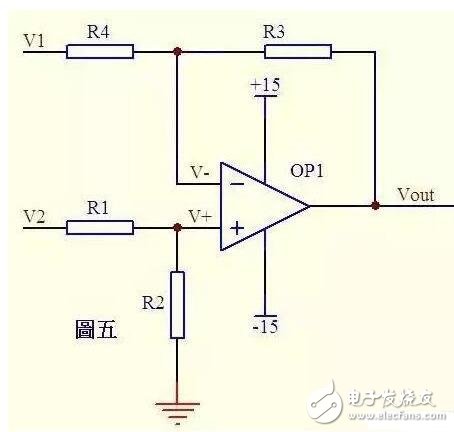
　　由虚断知，通过R1的电流等于通过R2的电流，同理通过R4的电流等于R3的电流，故：

　　（V2–V+）/R1=V+/R2……a

　　（V1–V-）/R4=（V—Vout）/R3……b

　　如果R1=R2，则：

　　V+=V2/2……c

　　如果R3=R4，则：

　　V-=（Vout+V1）/2……d

　　由虚短知：

　　V+=V-……e

　　所以Vout=V2-V1，这就是传说中的减法器了。

　　3、积分电路

　　

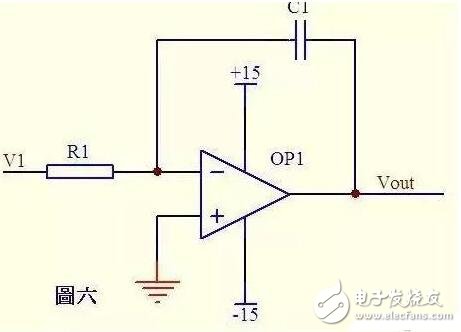
　　电路中，由虚短知，反向输入端的电压与同向端相等，由虚断知，通过R1的电流与通过C1的电流相等。

　　通过R1的电流：

　　i=V1/R1

　　通过C1的电流：

　　i=CdUc/dt=-CdVout/dt

　　所以，

　　Vout=（（-1/（R1*C1））∫V1dt

　　输出电压与输入电压对时间的积分成正比，这就是传说中的积分电路了。若V1为恒定电压U，则上式变换为：

　　Vout=-Ut/（R1C1）

　　t是时间，则Vout输出电压是一条从0至负电源电压按时间变化的直线。

　　4、微分电路

　　

　　由虚断知，通过电容C1和电阻R2的电流是相等的，由虚短知，运放同向端与反向端电压是相等的。则：

　　Vout=-iR2=-（R2C1）dV1/dt

　　这是一个微分电路。如果V1是一个突然加入的直流电压，则输出Vout对应一个方向与V1相反的脉冲。

　　5、电压电流转换检测电路

　　

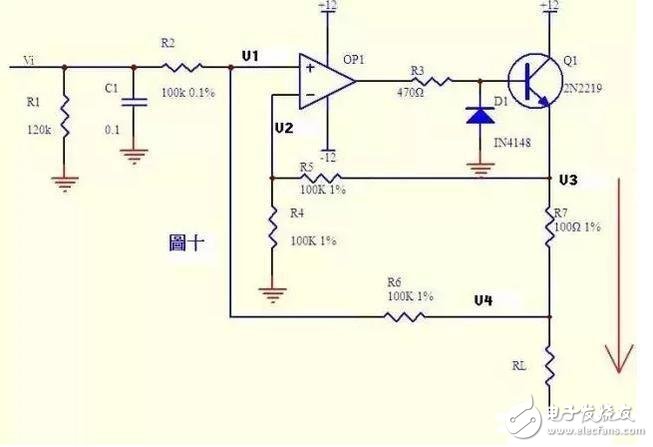
　　电流可以转换成电压，电压也可以转换成电流。图10就是这样一个电路。上图的负反馈没有通过电阻直接反馈，而是串联了三极管Q1的发射结，大家可不要以为是一个比较器就是了。只要是放大电路，虚短虚断的规律仍然是符合的！

　　由虚断知，运放输入端没有电流流过，则：

　　（Vi–V1）/R2=（V1–V4）/R6……a

　　同理：

　　（V3–V2）/R5=V2/R4……b

　　由虚短知：

　　V1=V2……c

　　如果R2=R6，R4=R5，则由abc式得：

　　V3-V4=Vi

　　上式说明R7两端的电压和输入电压Vi相等，则通过R7的电流：

　　I=Vi/R7

　　如果负载RL〈〈100KΩ，则通过Rl和通过R7的电流基本相同。