

卡诺图
电子常识
描述
卡诺图
卡诺图是逻辑函数的图形表示。利用卡诺图可以简化逻辑函数。
卡诺图的构成
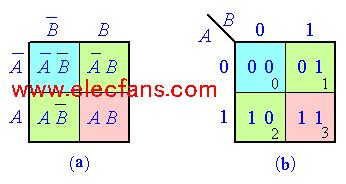
卡诺图是最小项按一定规律排列的方格图,每一个最小项占有一个小方格。因为最小项的数目与变量数有关,设变量数为n,则最小项的数目为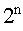 。二个变量的卡诺图见下图所示。图中第一行表示
。二个变量的卡诺图见下图所示。图中第一行表示 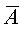 ,第二行表示A;第一列表示
,第二行表示A;第一列表示 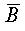 ,第二列表示B。这样四个小方格就由四个最小项分别对号占有,行和列的符号相交就以最小项的与逻辑形式记入该方格中。
,第二列表示B。这样四个小方格就由四个最小项分别对号占有,行和列的符号相交就以最小项的与逻辑形式记入该方格中。
三变量卡诺图
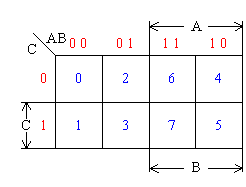
三变量卡诺图由8个最小项m0—m7组成,每个最小项占一个方格;
AB组合中左数位代表A变量,右数位代表B变量。沿横向从一个方格进行到下一个方格时,两个数位只变化一个; 原变量与非变量各占4格。
四变量卡诺图
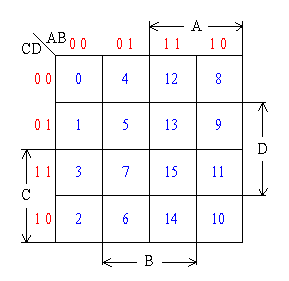
卡诺图二方格相邻组合
几何相邻的两个最小项是逻辑相邻的(两个最小项中只有一个变量不同);
有些方格几何上不相邻,但逻辑上却是相邻的;
任何两个最小项可以合并成最小项,且可减少一个变量。
【例3】四方格卡诺图中,有F(A,B,C,D)=∑m(2,3,8,10,12)
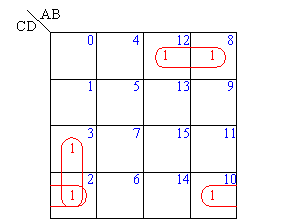
第一种组合方式:
| _ _ | ||
| m8+m12= | A C D | (几何相邻) |
| _ _ | ||
| m2+m3= | A B C | (几何相邻) |
| _ _ | ||
| m2+m10= | B C D | (几何不相邻,逻辑相邻) |
第二种组合方式:
| _ _ | ||
| m8+m12= | A C D | |
| _ _ | ||
| m2+m3= | A B C | |
| _ _ | ||
| m8+m10= | A B D | (几何不相邻,逻辑相邻) |
| F(A,B,C,D) | =∑m(2,3,8,10,12) |
| _ _ _ _ _ _ | |
| =A C D + A B C + B C D | |
| _ _ _ _ _ _ | |
| =A C D + A B C + A B D |
两种表达式虽然形式不同,但逻辑上是等价的。另外,m2、m8重复使用是允许的。
卡诺图四方格相邻组合
四方格相邻时,4个最小项可合并成1项,且可消去两个变量。
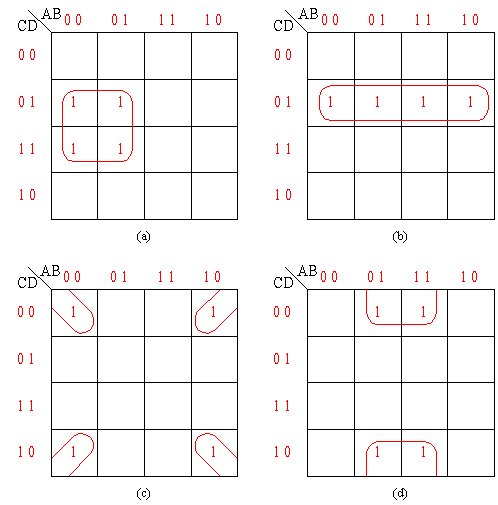
图(a)中,
| _ | |
| F(A,B,C,D)=∑m(1,3,5,7)= | AD |
图(b)中,
| _ | |
| F(A,B,C,D)=∑m(1,5,9,13)= | CD |
图(c)中,
| F(A,B,C,D)=∑m(0,2,8,10)= | ? |
图(d)中,
| F(A,B,C,D)=∑m(4,6,12,14)= | ? |
卡诺图八方格相邻组合
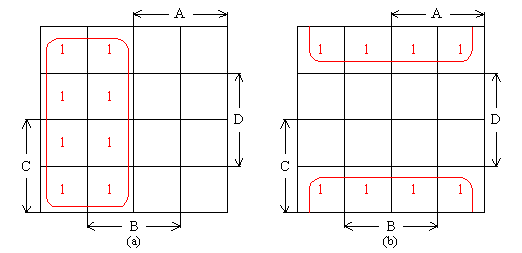
图(a)中,F(A,B,C,D)=∑m(0,1,2,3,4,5,6,7)=Ã
图(b)中,F(A,B,C,D)=∑m(0,4,12,8,2,6,14,10)=?
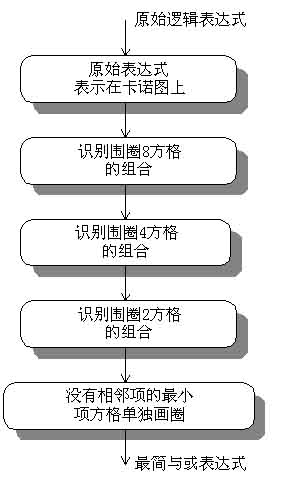
用卡诺图简化逻辑函数
简化规则
必须使每个方格(最小项)至少被包含一次;
使每个组合包含尽可能多的方格;
所有的方格包含在尽可能少的不同组合中。
简化步骤
无关项又叫任意项,是一种最小项,其值可以取0或1。利用无关项这一特点,可以使函数简化。
用卡诺图化简逻辑函数的步骤
如果表达式为最小项表达式,则可直接填入卡诺图
如表达式不是最小项表达式,但是“与—或表达式”,可将其先化成最小项表达式,再填入卡诺图。也可直接填入。
合并相邻的最小项,即根据下述原则画圈
尽量画大圈,但每个圈内只能含有2n(n=0,1,2,3……)个相邻项。要特别注意对边相邻性和四角相邻性。
圈的个数尽量少。
卡诺图中所有取值为1的方格均要被圈过,即不能漏下取值为1的最小项。
在新画的包围圈中至少要含有1个末被圈过的1方格,否则该包围圈是多余的。
写出化简后的表达式。每一个圈写一个最简与项,规则是,取值为l的变量用原变量表示,取值为0的变量用反变量表示,将这些变量相与。然后将所有与项进行逻辑加,即得最简与—或表达式。
在进行化简时,如果用图中真值为0的项更方便,可以用他们来处理,方法和真值取1时一样,只是结果要再做一次求反。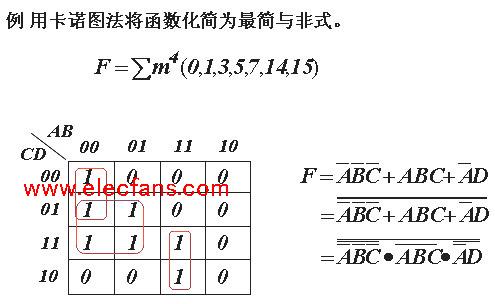
-
lxy7582935 2011-10-28
0 回复 举报好的,长知识了 收起回复
- 相关推荐
- 热点推荐
- 卡诺图
-
卡诺图在数字电路中的应用2025-01-14 2524
-
卡诺图如何化简2022-11-01 6568
-
数字逻辑基础卡诺图化简2019-05-30 3905
-
卡诺图化简法例题详解2018-03-07 331805
-
卡诺图简化方法及简化步骤介绍2018-03-01 60501
-
卡诺图小软件1.82016-12-17 1335
-
卡诺图化简逻辑函数.ppt2015-10-29 1288
-
降维卡诺图在逻辑函数设计中的应用2012-04-18 2073
-
次态卡诺图在时序逻辑电路中的应用2010-05-25 1031
-
卡诺图,卡诺图是什么意思2010-03-08 13279
-
卡诺图的构成及其简法2010-02-27 12854
-
卡诺图化简法2008-09-27 2257
-
逻辑函数的卡诺图化简法2008-01-21 823
全部0条评论

快来发表一下你的评论吧 !

