

典型二阶系统设计及其瞬态响应和稳定性分析
电子实验
描述
典型二阶系统设计及其瞬态响应和稳定性分析
一、 实验目的
1、掌握系统频率的测试方法、原理。
2、学会由开环系统对数频率特性,确定系统传递函数的方法。
二、 实验设备
硬件设备:微机一台,示波器一台,TDN-86/88—TDN-AC/ACS实验系统一套。
软件设备:Windows 2000操作平台,TDN-AC/ACS系统集成操作软件。
三、 实验原理

图3-1被测系统方框图
系统(或环节)的频率特性G(jω)是一个复变量,可以表示成以角频率ω为参数的幅值和相角:
G(jω)=︱G(jω)︱∠G(jω) (3-1)
本实验应用频率特性测试仪测量系统或环节的频率特性。
图3-1所示系统的开环频率特性为:
G1(jω) G2(jω) H(jω)=
(3-2)
采用对数幅频特性和相频特性表示,则式(3—2)表示为:
20lg︱G1(jω) G2(jω) H(jω) ︱= 20lg
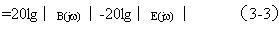
G1(jω) G2(jω) H(jω) = ∠

将频率特性测试仪内信号发生器产生的超低频正弦信号的频率从低到高变化,并施加于被测系统的输入端[r(t)],然后分别测量相应的反馈信号[b(t)]和误差信号[e(t)]的对数幅值和相位。频率特性测试仪测试数据经相关运算后在显示器中显示。
根据式(3-3)和式(3-4)分别计算出各个频率下的开环对数幅值和相位,在半对数坐标纸上做出实验曲线:开环对数幅频曲线和相频曲线。
根据实验开环对数幅频曲线画出开环对数幅频曲线的渐近线,再根据渐近线的斜率和转角确定频率特性(或传递函数)。所确定的频率特性(或传递函数)的正确性可以由测量的相频曲线来检验,对最小相位系统而言,实际测量所得的相频曲线必须与确定的频率特性(或传递函数)所画出的理论相频曲线在一定程度上相符。如果测量所得的相位在高频(相对于转角频率)时不等于-90o(q-p)[式中p和q分别表示传递函数分子和分母的阶次],那么,频率特性(或传递函数)必定是一个非最小相位系统的频率特性。
被测系统的模拟电路图:见图3-2

图3-2被测系统
四、 实验内容及步骤
测量系统的开环对数幅频曲线和相频曲线。
准备:将信号源单元(U1 SG)的ST插针和+5V插针用“短路块”短接。
实验步骤:
(1) 将频率测试仪中的信号发生器的频率调节为0.1MHz(正玄波),幅值调节至适当值,并施加至被测系统的输入端。
(2) 用示波器观察系统各环节波形,避免系统进入非线性状态。
(3) 测量系统误差信号[e(t)]的幅值(对数幅值,单位为分贝)和相位(度),并记录测量结果。
(4) 测量反馈信号[b(t)]的幅值(分贝)和相位(度)。
增大输入正弦信号的频率,直至300Hz,分别重复上述步骤。
表3-1 实验数据
|
输入U1(t)的频率 |
误差信号 |
反馈信号 |
开环频率特性 | |||||
|
幅值 |E(jω)| |
对数幅值 20lg|E(jω)| |
相位 ∠E(jω) |
幅值 |
对数幅值 |
相位 |
对数幅值 |
相位 | |
|
100mHz |
|
|
|
|
|
|
|
|
|
1Hz |
|
|
|
|
|
|
|
|
|
10Hz |
|
|
|
|
|
|
|
|
|
100Hz |
|
|
|
|
|
|
|
|
|
300Hz |
|
|
|
|
|
|
| |
实验中,由于传函是经拉氏变换推导出的,而拉氏变换是一种线性积分运算,因此它适用于线性定常系统,所以必须用示波器观察系统各环节波形,避免系统进入非线性状态。
实验中,系统输入正弦信号的幅值不能太大,否则反馈幅值更大,不易读出,同理,太小也不易读出。
五、 实验报告
1、 实验设备型号。
2、 实验目的。
3、 开环系统频率特性测试简要原理。
4、 被测系统模拟线路,实验数据。
5、 输入频率变化时的误差信号、反馈信号和开环频率特性的幅值和相位。
6、 画出各环节特性曲线,并进行结果分析。
-
buck电路的稳定性分析方法2024-11-21 2499
-
TINA可以进行运放的稳定性分析吗?2024-09-04 285
-
什么是二阶电路的零状态响应和零输入响应?零输入响应的步骤有哪些?2023-11-21 4930
-
如何保证二阶系统的稳定性?2021-06-24 2685
-
关于电源/负载电路组合的稳定性分析2021-05-11 2336
-
开关电源环路稳定性分析2020-05-31 3925
-
一阶电路和二阶电路的时域分析详细资料概述免费下载2018-07-25 1594
-
线性定常系统的瞬态响应和稳定性分析2016-09-01 1857
-
运放稳定性分析2016-02-19 969
-
LDO稳定性分析2011-11-01 862
-
频率响应法-相对稳定性分析2009-07-27 3438
-
二阶网络的零输入响应和零状态响应2009-05-10 3099
-
控制系统时域仿真和稳定性研究2008-10-16 2365
-
二阶动态电路响应的研究2008-09-24 6359
全部0条评论

快来发表一下你的评论吧 !

