

一种基于FPGA的快速静态光谱复原系统设计流程概述
可编程逻辑
描述
0 引言
在各类光谱测试中,对光谱数据采集的速度都有不同的要求,故提高光谱数据采集速度的技术主要有以下两大方向:一是通过光学方法实现,将传统时间扫描改成空间成像,由此可大幅提高干涉条纹采集速度[1];二是通过数据采集算法实现[2],利用高效算法完成数据快速运算。对于静态干涉系统而言,静态干涉条纹的采集是直接获取图像实现的,不需要机械扫描,所以大幅提高了速度。其将待测光以静态干涉条纹的方式成像在CCD上,由此空域到频域完成了光谱分布的计算[3-6]。可见制约干涉系统数据处理能力的主要是系统硬件部分和处理算法的优劣。
FPGA作为基于硬件编程的数据处理芯片,在众多光谱数据处理方面具有显著的特点与优势[7-10]。因为FPGA处理速度快、功耗低,所以被广泛用于信号处理等。静态光谱数据的运算与处理耗时最多的是傅氏变换运算部分,其包括了乘法运算和转移匹配处理,故使用FPGA完成可尽量保障系统的运算实时性。通过FPGA设计完成对芯片资源利用率的最优化,这样可以在不降低运算速度的前提下最大程度地节约成本。
为了将静态干涉条纹的空域信息通过算法转换为频域信息,本文研究了适用于FPGA的干涉条纹数据采集与处理系统,该系统速度快、稳定性高,具有高效性、稳定性的特点[11-12]。相比之下,FPGA比Xilinx更快,资源利用率更高。将本系统与MATLAB仿真结果进行对比可知,本系统光谱数据计算效果更好、误差更小,具有更好的应用前景。
1 系统设计
光谱数据采集与处理系统如图1所示。首先,光学接收模块采集入射光,经准直后进入静态干涉棱镜中,产生静态干涉条纹,再通过CCD传感器完成对干涉条纹的采集。CCD的采集速度由FPGA决定,保证采集与系统运算的同步性,当干涉条纹数据进入FPGA处理模块后,完成对初始光的光谱重建。由傅氏变换关系可知,入射光的两束分束光通过准直透镜以后被分离,从而形成干涉过程需要的两束光,这两束光最后汇聚到了一起,因为不同的光程差而形成干涉条纹。FPGA对干涉条纹采集并处理,包括滤波、降噪、FFT、光谱位置标定等,最终实现将频域信息转换成光谱信息。
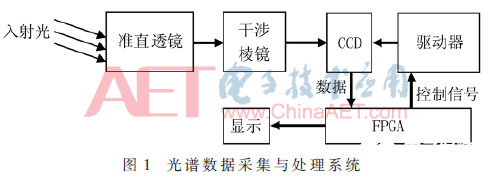
FPGA的运算速度快,适合光谱的快速计算,FPGA内部逻辑设计十分重要,其决定了系统是否能够高效地完成数据采集与处理。FPGA的运算数据处理部分主要对空域信息进行解算,从而实现对频域信息的计算,是提高其运算处理能力的主要手段。FPGA的数据处理需要从控制CCD探测器开始,对数据的高效计算包括干涉条纹采集、数据傅氏变换、光谱位置标定等,通过以上思路完成了对FPGA硬件模块结构的设计,如图2所示。
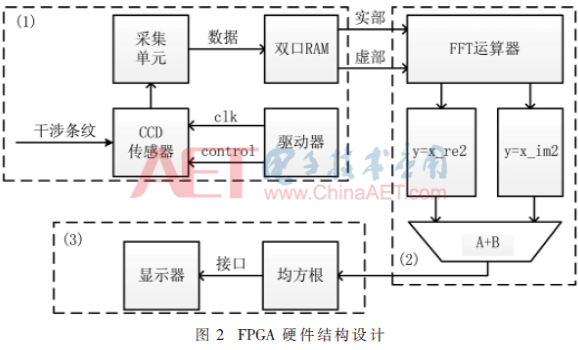
整个光谱数据采集与处理系统可以分为三个部分:数据采集区、数据处理区和数据显示单元。(1)数据采集区,该区域通过驱动控制电路使CCD探测器将干涉条纹传输给存储器,存储器采用双口RAM设计,以便实现数据的高速输入与输出,将实部与虚部分开发送给FFT运算器;(2)数据处理区,该区域将数据中实部和虚部分别进行数据蝶形运算,再对蝶形运算结果进行乘法混合,为了进一步提高系统处理能力,与双端口RAM进行更好的配合,采用了并行数据输入输出的形式完成,光谱位置的标定通过Square root模块实现,大大提升了系统的处理能力;(3)数据显示单元,该单元将处理完成的数据通过预先设定的接口完成数据的输出与显示。
2 采集接口设计及仿真
为了实现快速获取光频谱信息,需要干涉条纹的采集速度大于处理速度,同时,还需要将采样数据与处理数据进行匹配。可见,在实现FFT过程中,需要提高数据的传输速率。在本系统中,数据处理模块为了保障FFT运算过程的连续性,系统数据传输速率设置为3.0 MHz(读)和1.5 MHz(写)。由此可见,读写采用异步RAM实现,数据深度均为10位。输入采用“addra”和“addrb”、时钟采用“clka”和“clkb”、数据输出采用“doutb”实现。则其异步存储模块的仿真结果如图3所示。
在光谱数据采集模块中,采用TOSHIBA公司的TVD-2712型CCD传感器,位深设置可选8 bit、10 bit、12 bit,位深越深对应的光谱量化误差越小,但是其数据总量越大,所以通过不同位深的仿真计算,可以优化位深的选择,从而确定系统数据转换位深设置。当处理系统的位深采用10 bit时,时钟频率为150 MHz,则CCD图像传感器的最高采集频率可以达到10 MHz,由此可见,设计20分频的系统分频结构具有较好的匹配效果。首先,利用Verilog触发系统控制端,形成驱动信号控制,然后在Modelsim6.0中仿真,仿真结果如图3所示。根据仿真结果可知,设计的时序逻辑关系与拟采用的CCD逻辑时序是一致的,系统构成的读写异步RAM可完成系统光谱数据的采集与处理,对静态干涉条纹的采集、传输、处理具有高效性。
3 处理模块设计及仿真
光谱数据处理采用Virtex 2-Pro型嵌入式处理芯片实现,流水线处理模式,位深选择10 bit,FFT在FPGA的IP核中实现,输入采用“xn_im”和“xn_re”,起始信号为“start”,输出信号采用“xk_im”、“xk_re”、“xk_index”、“xk_index”完成实部虚部信息的输出。运算流程为基-2时间型。FPGA的时序关系仿真结果如图4所示。
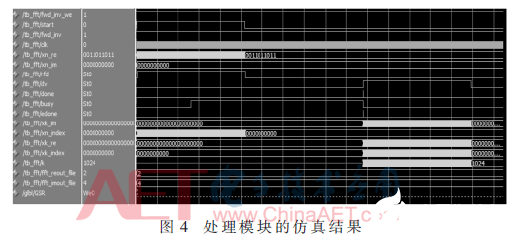
在该运算器中,通过两个辅助的RAM可以实现对变换结果的存储,利用RAM减小对提高FPGA资源使用效率,进而提升系统的处理能力。系统由两个硬件乘法器、四个储存器完成了光谱数据的蝶形运算与光谱位置标定,同时,该方法还有效地提高了系统的数据处理速率,在100.0 MHz的工作基频下,实现1 024点FFT仅需33 μs。同时,还在仿真中对不同位深数据进行了测试,仿真结果表明,位深主要影响系统的处理速度,8 bit速度最快,12 bit速度最慢,但8 bit的反演结果波长振幅降低,信噪比低;10 bit与12 bit的振幅和信噪比相近,但12 bit运算时长明显增加,为了保证反演的实时性,最终选用10 bit,在下面的实验中将进行进一步对比。
4 实验
4.1 实验条件
整个系统由激光光源、CCD传感器、干涉棱镜、高速数据采集卡、FPGA开发板组成,计算机完成在片编译及仿真分析;激光器的中心波长是980 nm,提供稳定的待测激光;干涉棱镜采用两个直角棱镜的组合,其中一个存在等效斜契角0.10°;示波器采集控制信号;TVD2712型CCD传感器采集静态干涉条纹,该CCD的光谱范围为320~1 100 nm,单个像元尺寸为8 μm×8 μm。系统整体结构如图5所示。

4.2 位深对比实验
在仿真分析后,通过构建硬件测试系统完成对中心波长980 nm激光的光谱复原。在测试前,设定了合适的位深格式数据,再实现对光谱数据的测试。实验对数据的位深是调试后选定的,针对8 bit、10 bit和12 bit的测试数据结果可知,不同位深测试得到的中心波长处振幅不同,实现时间不同,测试结果如图6所示。
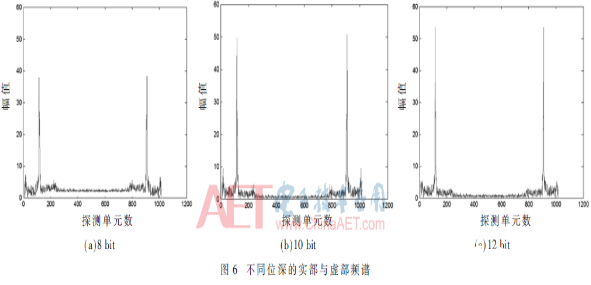
位深档位不同时,从8 bit调整为12 bit时,经傅氏变换后的中心波长处主峰振幅不断增大,信噪比更高,但变化过程逐渐趋缓;当位深增大时,测试得到的中心波长位置不变,半宽也没有明显变化;同时,当位深增大时,运算时间却明显提升,系统总体运算时间从约1 200个机器周期增至5 200个机器周期。可见,单纯通过提高位深不会改变中心波长位置和半宽,但其可以使光谱振幅得到提高,从而提升信噪比。但代价是系统的运算时间进一步增长,不利于系统的实时处理。所以位深的设置需要综合考虑,系统最终采用10 bit的位深,同时保证系统一定的信噪比和处理速度。
4.3 频谱对比实验
在位深测试完成的基础上,分别对两种不同处理方式同时针对980 nm进行对比分析,分析系统光谱复原处理效果,与传统的MATLAB软件光谱反演方法进行对比。系统获得的静态干涉条纹如图7(a)所示,通过FPGA复原得到的实部与虚部数据如图7(b)所示,通过MATLAB复原得到的实部与虚部数据如图7(c)所示。
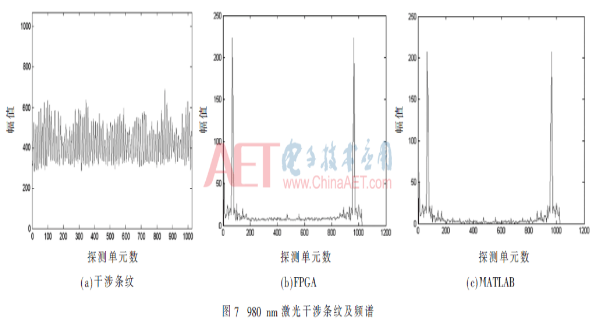
如图7所示,图7(a)表示由干涉棱镜获得的静态干涉条纹,该干涉条纹由FPGA采集并传输到采集卡,再通过传输接口完成与电脑的数据交互。图7(b)和图7(c)是对同一组光谱数据的复原结果,FPGA与MATLAB的光谱反演中心波长位置相同,误差小于0.2 nm;但FPGA获得的振幅峰峰值要略优于MATLAB,因为其叠加效果更为明显;FPGA获得的数据噪声均值不如MATLAB的测试数据;10 bit位深条件下FPGA的整个数据处理周期为55 μs,而MATLAB的整个数据处理周期为610 μs,可见,采用本系统与传统处理算法上光谱反演效果基本一致,而在处理速度上得到了大幅提高,说明系统设计符合设计要求。
5 结论
针对干涉条纹数据处理中处理效果与处理速度之间的矛盾问题,设计了一种基于FPGA的快速静态光谱复原系统。设计了FPGA的采集与处理硬件模块,通过FPGA实时控制CCD传感器快速获取干涉条纹,再经处理模块完成蝶形运算与光谱位置标定等。通过对采集、处理部分的设计与仿真,通过时序逻辑关系结果验证了本系统的可行性。在对比了不同位深对系统复原效果的基础上,选择了10 bit的工作模式,并与MATLAB测试数据比较验证了本系统的精度与特性,说明其具有较好的应用前景。
参考文献
[1] MANZARDO O,HERZIG H P,CULDIMANN B,et al.New design for an integrated Fourier transform spectrometer[C].Proceeding of SPIE,2000,4178:310-319.
[2] 周志娟,张玉贵,樊奔。基于FPGA的干涉信号双ADC采集系统设计[J]。电子测量技术,2016,12(4):123-128.
[3] KAZUMASA T,HIROTAKA A,KATSUNARI O.Correction for phase-shift deviation in a complex Fourier transform integrated-optic spatial heterodyne spectrometer with an active phase-shift scheme[J].Optics Letters,2011,36(7):1044-1046.
[4] 李岩,徐金甫。基于新型FPGA的FFT设计与实现[J]。计算机工程与应用,2007,43(14):102-104.
[5] Li Xiao,Zhang Jilong,Tian Erming.Passive laser spectrum detection technology based on static interferometer[C].2008 International Conference of Optical Instrument and Technology,Proceedings.of SPIE,2008,7160:11-15.
[6] ALESSANDRO R,MARCO D,GIOVANNI C.Bilateral filter-based adaptive non-uniformity correction for infrared focal-plane array systems[J].Optical Engineering,2010,49(5):057003.
[7] 贺刚,柏鹏,彭卫东,等。一种基于IP核通信系统中滑动相关捕获算法的FPGA实现[J]。江西师范大学学报(自然科学版),2011,35(2):151-154.
[8] 陈珂,刘学聪,罗先卫,等.32通道光纤阵列式高灵敏飞秒激光光谱分析仪[J]。光电子·激光,2015,26(1):116-119.
[9] 郭嘉,卢启鹏,高洪智,等。基于FPGA的无创伤血液成分光谱采集系统设计[J]。光谱学与光谱分析,2016,36(9):2991-2996.
[10] 吕默,陈晨,王一丁。用于中红外痕量气体检测的光电信号高速采集系统设计[J]。激光杂志,2016,37(2):26-29.
[11] MILES A J,WIEN F,LEES J G.Calibration and stand-ardization of synchrotron radiation and conventional circular dichroism spectrometers.Part 2:Factors affecting magnitude and wavelength[J].Spectroscopy-AN International Journal,2005,19(1):43-51.
[12] 张多利,沈休垒,宋宇鲲,等。基于异构多核可编程系统的大点FFT卷积设计与实现[J]。电子技术应用,2017,43(3):16-20.
- 相关推荐
- 热点推荐
- FPGA
-
一种基于FPGA-的步进电机控制系统的设计2022-06-23 725
-
介绍一种基于FPGA的电机控制系统2022-02-17 977
-
一种新型的高光谱图像解混算法2021-06-27 794
-
求大佬分享一种多光谱可见光遥感图像压缩系统的设计方案2021-06-02 1334
-
Nexar如何为FPGA设计提供一种全新的方法?2021-05-08 1666
-
FPGA应用设计中一种崭新的硬宏开发流程是怎样的2021-05-06 843
-
如何使用FPGA实现图像采集系统中色彩复原模块2021-04-01 1030
-
FPGA基本开发流程概述2019-01-28 2676
-
一种基于FPGA的直扩系统快速捕获算法_杨峰2017-03-19 577
-
一种基于FPGA的双接口NFC芯片验证系统2017-01-03 730
-
一种便携式光谱采集系统的设计与实现2013-04-15 950
-
Hadamard变换光谱仪光谱复原算法的FPGA实现2011-08-15 927
-
一种面向FPGA的快速HOUGH变换2011-03-16 1616
-
基于多DSP的干涉超光谱复原系统设计2010-01-06 365
全部0条评论

快来发表一下你的评论吧 !

