如何降低FM数字解调门限

本文先是简单介绍FM的基本原理，一般的数字解调方案，指出FM解调门限的存在，并且给出了仿真结果；接着详细讨论了噪声问题，指出噪声的自相关特性与通道滤波器的关系，并根据噪声的这些性质提出了一种新的数字解调方案，最后是新方案的实际仿真结果。

FM的基本原理
FM 是把信号调制到载波的频率参数上，瞬时频率与平均频率的差是信号，表达式如下：

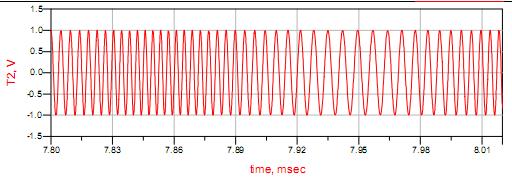
下图是利用 ADS 产生的 FM 信号时域与频域波形，从时域波形能很明显看到 FM 的恒包络特
征，瞬时频率随时间变化特征。这里产生的 FM 载波频率为 200KHz，单声道，调制信号为
5KHz 点频，调制度为 65KHz，没有考虑预加重。

图 1：FM信号的频域波形

time, msec 
图 2：FM信号的时域波形
FM的简单数字解调与门限效应
利用数字方式对 FM 信号解调，原理上就是计算瞬时频率，瞬时频率是相位的导数，在数
字中导数用一阶差分替代，下面是一个简单的 FM数字解调框图：

利用上面这种简单解调方式，我们调整输入信噪比，看输出信噪比的变化，可以清楚的看
到门限的存在，下面是仿真数据和曲线图形：
表 1：简单数字解调输入 SNR与输出 SNR关系，此处 FM调制度为 22K，单声道
 
SNR in  5  6  7  8  9  10  11  12  13  18  23  28
SNRout  9.5  12.8  16.5  20.2  23.4 24.5 25.6 26.6 27.6 32.7  37.7  42.6

图 4：FM解调原理图
注意上面没有考虑去加重对信噪比的改善，噪声是考虑 1.5k~15K 带宽内噪声。输入噪声
是滤波器带宽内的噪声，信道滤波器按 70K 计算的。由上面曲线明显看到在输入信噪比
9dB 以下时，输出 SNR 与输入 SNR 不再是线性关系，输入信号在 9dB 处有一个拐角，称该
点为这种解调方案的解调门限。
从 IQ 平面可以比较容易理解解调门限的存在，如下图，当信噪比较低时，噪声矢量有时
会大于信号矢量，造成相位 180 度的变化，从而造成噪声迅速增加，就形成了门限，一般
弱信号受限于接收机噪声系数，而噪声系数反映的噪声符合高斯分布，从高斯分布的函数
看，超过 3 倍标准差的情况非常少，也就是说当 SNR 大于 20log(3)时，很少有 180 度翻
转情况，这样 20log(3)就成了 FM 的解调门限。20log(3)=9.5dB，与上面的仿真曲线吻合
非常好。

图 5：FM解调门限示意图
噪声自相关特性与噪声预测
接收机接收弱信号所受限的噪声一般是接收机热噪，电流噪声等，这些噪声对我们的信号
带宽而言可以算是白色噪声，这也就意味着噪声前后不相关，幸运的是接收通道都有信道
选择滤波器，在数字判决的时候，噪声前后是相关的，因为这种相关性是有接收通道滤波
器引起的，所以噪声的自相关函数就等于滤波器冲击响应的自相关函数，其公式如下：

上式中 h(t)是通道滤波器的时域冲击响应。因为一般接收机的通道滤波器是固定的，这
样噪声的自相关特性也就确定下来了。
如果 t1 时刻噪声电压为 n1，t2 时刻噪声电压为 n2，那么 t3 时刻的噪声电压该是多少？
在这里我们可以将 t3 时刻的噪声电压 n3 做一个分解，分出与以前相关的部分和不相关的
部分，如下式：

根据前面讨论的噪声相关特性我们可以得到下面几个方程：

图 6：噪声预测和抵消示意图
上图中的 c1,c2,c3,…是与信道滤波器相关的参数，如果上图中没有信道滤波器，则噪声
前后不相关，这些系数全部是 0。前面方程 5 至方程 10 已经讲了两阶情况的系数求法，
此处不在赘述。下面是利用 ADS 做的仿真结果，此处滤波器带宽为 70K，数字时钟用的是
500K，噪声预测模型是两阶的，因为通过分析发现噪声差 3个时钟就基本不相关了。

图 7：噪声抵消示意图
上图中红色的是抵消之前的频域和时域噪声波形，蓝色的是抵消之后的频域和时域噪声波
形，有此处看到噪声功率被抑制了很多。利用噪声抵消有很大好处，但前提是必须相对精
确地找到噪声分量，也就是找出采样点里面的信号分量。信号与噪声是合在一起的，如要
把它们分出来，就需要一个判决过程，针对数字通信，这个判决往往比较明显，如 QPSK
解调，在判决时，只要看(I,Q)，如果落在了第一象限，我们就判它是(1,1)，落在第二象
限，我们就判它是(-1，1)，理想星座点到实际 IQ的向量就是噪声分量，如下图所示：

FM信号的判决与噪声抵消
通过上面的讨论，我们可以整理出这样一个接收机模型，如下图：

前面已经讨论过噪声预测和数字通信中的判决，针对 FM 信号，该如何判决？FM 信号没有
数字通信常有的最佳判决时刻，但 FM 有一个非常明显的特征，理想 FM 是恒包络的，我们
根据这一特征可以做一个判决，很明显这种判决不能完全区分噪声和信号，因为噪声的切
向分量无法从信号里面分出来，尽管如此，这种判决还是可以比较好的解决 FM 解调门限
问题。通过下面图形可以比较容易理解这种判决，并了解它的局限性：

图 10：FM基于恒包络特性的判决示意图
从上图看到，理想的噪声分量为 n1，而我们仅找出了法向噪声分量 n1r，n1t 确无法识别
出来，这就是这种判决的局限所在。利用这种判决原理我们搭建了下面仿真电路图，并做
了仿真分析：

图 12：新旧数字解调方案性能对比
上图蓝色的是新解调方案性能曲线，对比看到新解调方案可以将解调门限降低 1dB，在弱
场接收时，输出信噪比提高了 3dB。