

使用numpy Python库从零开始构建人工神经网络
电子说
描述
为何从零开始?
有许多深度学习库(Keras、TensorFlow和PyTorch等)可仅用几行代码构建一个神经网络。然而,如果你真想了解神经网络的底层运作,建议学习如何使用Python或任何其他编程语言从零开始为神经网络编程。
不妨创建某个随机数据集:
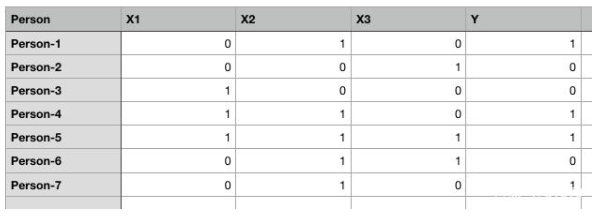
图1. 为简单起见,随机数据集带二进制值
上面表格有五列:Person、X1、X2、X3和Y。1表示true,0表示false。我们的任务是创建一个能够基于X1、X2和X3的值来预测Y值的人工神经网络。
我们将创建一个有1个输入层、1个输出层而没有隐藏层的人工神经网络。开始编程前,先不妨看看我们的神经网络在理论上将如何执行:
ANN理论
人工神经网络是一种监督式学习算法,这意味着我们为它提供含有自变量的输入数据和含有因变量的输出数据。比如在该示例中,自变量是X1、X2和X3,因变量是Y。
首先,ANN进行一些随机预测,将这些预测与正确的输出进行比较,计算出误差(预测值与实际值之间的差)。找出实际值与传播值之间的差异的函数名为成本函数(cost function)。这里的成本指误差。我们的目标是使成本函数最小化。训练神经网络基本上是指使成本函数最小化。下面会介绍如何执行此任务。
神经网络分两个阶段执行:前馈阶段和反向传播阶段。下面详细介绍这两个步骤。
前馈
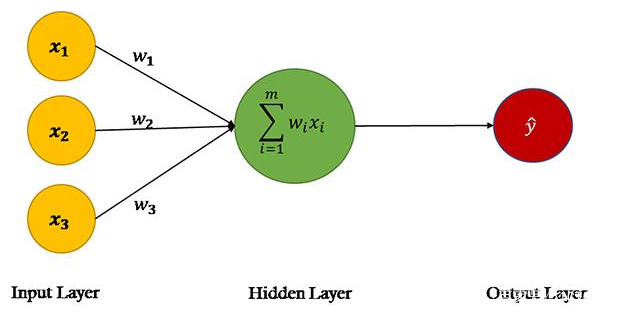
图2
来源:单层神经网络,又叫Perceptron
在ANN的前馈阶段,基于输入节点中的值和权重进行预测。如果看一下上图中的神经网络,会看到数据集中有三个特征:X1、X2和X3,因此第一层(又叫输入层)中有三个节点。
神经网络的权重基本上是我们要调整的字符串,以便能够正确预测输出。请记住,每个输入特性只有一个权重。
以下是在ANN的前馈阶段所执行的步骤:
第1步:计算输入和权重之间的点积
输入层中的节点通过三个权重参数与输出层连接。在输出层中,输入节点中的值与对应的权重相乘并相加。最后,偏置项b添加到总和。
为什么需要偏置项?
假设某个人有输入值(0,0,0),输入节点和权重的乘积之和将为零。在这种情况下,无论我们怎么训练算法,输出都将始终为零。因此,为了能够做出预测,即使我们没有关于该人的任何非零信息,也需要一个偏置项。偏置项对于构建稳健的神经网络而言必不可少。
数学上,点积的总和:
X.W=x1.w1 + x2.w2 + x3.w3 + b
第2步:通过激活函数传递点积(X.W)的总和
点积XW可以生成任何一组值。然而在我们的输出中,我们有1和0形式的值。我们希望输出有同样的格式。为此,我们需要一个激活函数(Activation Function),它将输入值限制在0到1之间。因此,我们当然会使用Sigmoid激活函数。
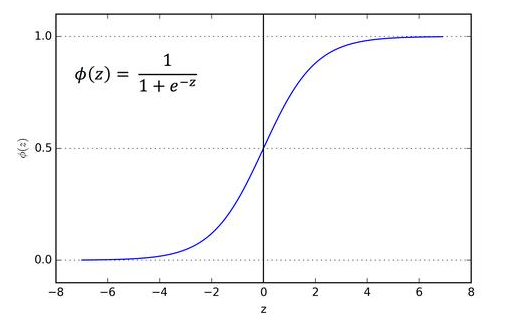
图3. Sigmoid激活函数
输入为0时,Sigmoid函数返回0.5。如果输入是大正数,返回接近1的值。负输入的情况下,Sigmoid函数输出的值接近零。
因此,它特别适用于我们要预测概率作为输出的模型。由于概念只存在于0到1之间,Sigmoid函数是适合我们这个问题的选择。
上图中z是点积X.W的总和。
数学上,Sigmoid激活函数是:
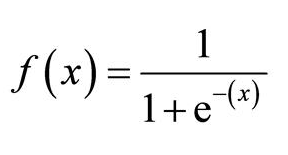
图4. Sigmoid激活函数
总结一下到目前为止所做的工作。首先,我们要找到带权重的输入特征(自变量矩阵)的点积。接着,通过激活函数传递点积的总和。激活函数的结果基本上是输入特征的预测输出。
反向传播
一开始,进行任何训练之前,神经网络进行随机预测,这种预测当然是不正确的。
我们先让网络做出随机输出预测。然后,我们将神经网络的预测输出与实际输出进行比较。接下来,我们更新权重和偏置,并确保预测输出更接近实际输出。在这个阶段,我们训练算法。不妨看一下反向传播阶段涉及的步骤。
第1步:计算成本
此阶段的第一步是找到预测成本。可以通过找到预测输出值和实际输出值之间的差来计算预测成本。如果差很大,成本也将很大。
我们将使用均方误差即MSE成本函数。成本函数是找到给定输出预测成本的函数。
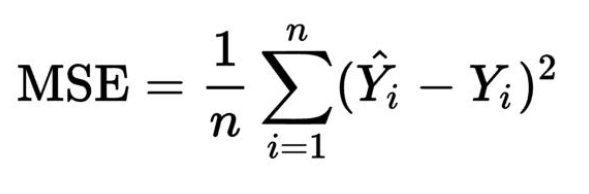
图5. 均方误差
这里,Yi是实际输出值,i是预测输出值,n是观察次数。
第2步:使成本最小化
我们的最终目的是微调神经网络的权重,并使成本最小化。如果你观察仔细,会了解到我们只能控制权重和偏置,其他一切不在控制范围之内。我们无法控制输入,无法控制点积,无法操纵Sigmoid函数。
为了使成本最小化,我们需要找到权重和偏置值,确保成本函数返回最小值。成本越小,预测就越正确。
要找到函数的最小值,我们可以使用梯度下降算法。梯度下降可以用数学表示为:

图6. 使用梯度下降更新权重
Error是成本函数。上面的等式告诉我们找到关于每个权重和偏置的成本函数的偏导数,然后从现有权重中减去结果以得到新的权重。
函数的导数给出了在任何给定点的斜率。为了找到成本是增加还是减少,给定权重值,我们可以找到该特定权重值的函数导数。如果成本随重量增加而增加,导数将返回正值,然后将其从现有值中减去。
另一方面,如果成本随重量增加而降低,将返回负值,该值将被添加到现有的权重值中,因为负负得正。
在上面公式中,a名为学习速率,乘以导数。学习速率决定了我们的算法学习的速度。
我们需要对所有权重和偏置重复执行梯度下降操作,直到成本最小化,并且成本函数返回的值接近零。
现在是实现我们迄今为止研究的人工神经网络的时候了。我们将用Python创建一个简单的神经网络,有1个输入层和1个输出层。
使用numpy实现人工神经网络
图7
图片来源:hackernoon.com
要采取的步骤:
1.定义自变量和因变量
2.定义超参数
3.定义激活函数及其导数
4.训练模型
5.做出预测
第1步:先创建自变量或输入特征集以及相应的因变量或标签。
#Independent variables
input_set = np.array([[0,1,0],
[0,0,1],
[1,0,0],
[1,1,0],
[1,1,1],
[0,1,1],
[0,1,0]])#Dependent variable
labels = np.array([[1,
0,
0,
1,
1,
0,
1]])
labels = labels.reshape(7,1) #toconvert labels to vector
我们的输入集含有七个记录。同样,我们还创建了一个标签集,含有输入集中每个记录的对应标签。标签是我们希望ANN预测的值。
第2步:定义超参数。
我们将使用numpy的random.seed函数,以便在执行以下代码时可以获得同样的随机值。
接下来,我们使用正态分布的随机数初始化权重。由于输入中有三个特征,因此我们有三个权重的向量。然后,我们使用另一个随机数初始化偏置值。最后,我们将学习速率设置为0.05。
np.random.seed(42)
weights = np.random.rand(3,1)
bias = np.random.rand(1)
lr = 0.05 #learning rate
第3步:定义激活函数及其导数:我们的激活函数是Sigmoid函数。
def sigmoid(x):
return 1/(1+np.exp(-x))
现在定义计算Sigmoid函数导数的函数。
def sigmoid_derivative(x):
return sigmoid(x)*(1-sigmoid(x))
第4步:是时候训练ANN模型了。
我们将从定义轮次(epoch)数量开始。轮次是我们想针对数据集训练算法的次数。我们将针对数据训练算法25000次,因此epoch将为25000。可以尝试不同的数字以进一步降低成本。
for epoch in range(25000):
inputs = input_set
XW = np.dot(inputs, weights)+ bias
z = sigmoid(XW)
error = z - labels
print(error.sum())
dcost = error
dpred = sigmoid_derivative(z)
z_del = dcost * dpred
inputs = input_set.T
weights = weights - lr*np.dot(inputs, z_del)
for num in z_del:
bias = bias - lr*num
不妨了解每个步骤,然后进入到预测的最后一步。
我们将输入input_set中的值存储到input变量中,以便在每次迭代中都保留input_set的值不变。
inputs = input_set
接下来,我们找到输入和权重的点积,并为其添加偏置。(前馈阶段的第1步)
XW = np.dot(inputs, weights)+ bias
接下来,我们通过Sigmoid激活函数传递点积。(前馈阶段的第2步)
z = sigmoid(XW)
这就完成了算法的前馈部分,现在是开始反向传播的时候了。
变量z含有预测的输出。反向传播的第一步是找到误差。
error = z - labels
print(error.sum())
我们知道成本函数是:
图8
我们需要从每个权重方面求该函数的微分,这可以使用微分链式法则(chain rule of differentiation)来轻松完成。我将跳过推导部分,但如果有人感兴趣,请留言。
因此,就任何权重而言,成本函数的最终导数是:
slope = input x dcost x dpred
现在,斜率可以简化为:
dcost = error
dpred = sigmoid_derivative(z)
z_del = dcost * dpred
inputs = input_set.T
weights = weight-lr*np.dot(inputs, z_del)
我们有z_del变量,含有dcost和dpred的乘积。我们拿输入特征矩阵的转置与z_del相乘,而不是遍历每个记录并拿输入与对应的z_del相乘。
最后,我们将学习速率变量lr与导数相乘,以加快学习速度。
除了更新权重外,我们还要更新偏置项。
for num in z_del:
bias = bias - lr*num
一旦循环开始,你会看到总误差开始减小;训练结束时,误差将保留为很小的值。
-0.001415035616137969
-0.0014150128584959256
-0.0014149901015685952
-0.0014149673453557714
-0.0014149445898578358
-0.00141492183507419
-0.0014148990810050437
-0.0014148763276499686
-0.0014148535750089977
-0.0014148308230825385
-0.0014148080718707524
-0.0014147853213728624
-0.0014147625715897338
-0.0014147398225201734
-0.0014147170741648386
-0.001414694326523502
-0.001414671579597255
-0.0014146488333842064
-0.0014146260878853782
-0.0014146033431002465
-0.001414580599029179
-0.0014145578556723406
-0.0014145351130293877
-0.0014145123710998
-0.0014144896298846701
-0.0014144668893831067
-0.001414444149595611
-0.0014144214105213174
-0.0014143986721605849
-0.0014143759345140276
-0.0014143531975805163
-0.001414330461361444
-0.0014143077258557749
-0.0014142849910631708
-0.00141426225698401
-0.0014142395236186895
-0.0014142167909661323
-0.001414194059027955
-0.001414171327803089
-0.001414148597290995
-0.0014141258674925626
-0.0014141031384067547
-0.0014140804100348098
-0.0014140576823759854
-0.0014140349554301636
-0.0014140122291978665
-0.001413989503678362
-0.001413966778871751
-0.001413944054778446
-0.0014139213313983257
-0.0014138986087308195
-0.0014138758867765552
-0.0014138531655347973
-0.001413830445006264
-0.0014138077251906606
-0.001413785006087985
-0.0014137622876977014
-0.0014137395700206355
-0.0014137168530558228
-0.0014136941368045382
-0.0014136714212651114
-0.0014136487064390219
-0.0014136259923249635
-0.001413603278923519
-0.0014135805662344007
-0.0014135578542581566
-0.0014135351429944293
-0.0014135124324428719
-0.0014134897226037203
-0.0014134670134771238
-0.0014134443050626295
-0.0014134215973605428
-0.0014133988903706311
第5步:作出预测
是时候作出一些预测了。先用[1,0,0]试一下:
single_pt = np.array([1,0,0])
result = sigmoid(np.dot(single_pt, weights) + bias)
print(result)
输出:
[0.01031463]
如你所见,输出更接近0而不是1,因此分类为0。
不妨再用[0,1,0]试一下:
single_pt = np.array([0,1,0])
result = sigmoid(np.dot(single_pt, weights) + bias)
print(result)
输出:
[0.99440207]
如你所见,输出更接近1而不是0,因此分类为1。
结论
我们在本文中学习了如何使用numpy Python库,从零开始创建一个很简单的人工神经网络,只有1个输入层和1个输出层。该ANN能够对线性可分离数据进行分类。
如果我们有非线性可分离的数据,我们的ANN就无法对这种类型的数据进行分类。下篇将介绍如何构建这样的ANN。
-
人工神经网络原理及下载2008-06-19 0
-
人工神经网络课件2016-06-19 0
-
【PYNQ-Z2试用体验】神经网络基础知识2019-03-03 0
-
人工神经网络实现方法有哪些?2019-08-01 0
-
如何构建神经网络?2021-07-12 0
-
嵌入式中的人工神经网络的相关资料分享2021-11-09 0
-
不可错过!人工神经网络算法、PID算法、Python人工智能学习等资料包分享(附源代码)2023-09-13 0
-
基于Numpy实现同态加密神经网络2018-03-27 7970
-
从零开始学习用Python构建神经网络2018-05-30 10695
-
如何使用numpy库从零开始创建循环神经网络模型2020-12-10 1733
-
PyTorch教程之从零开始的递归神经网络实现2023-06-05 335
-
卷积神经网络python代码2023-08-21 1042
-
如何使用Python进行神经网络编程2024-07-02 422
-
Python自动训练人工神经网络2024-07-19 376
-
如何使用Python构建LSTM神经网络模型2024-11-13 439
全部0条评论

快来发表一下你的评论吧 !

