

手把手教系列之IIR数字滤波器设计实现
嵌入式设计应用
描述
(在此特别鸣谢作者 逸珺 及其 公众号“嵌入式客栈”)【导读】:在嵌入式系统中经常需要采集模拟信号,采集模拟信号的信号链中难免引入干扰,那么如何滤除干扰呢?今天就来个一步一步描述如何设计部署一个IIR滤波器到你的系统。写这篇文章考虑到很多粉丝是做单片机系统开发的,经常会需要采集模拟信号,系统中往往存在各种各样的干扰,干扰常常让人一筹莫展,所以花了一周时间整理出IIR滤波器设计部署的干货文章,照此一步一步做,你必会解决大部分干扰问题。
逸珺编外语:文章写作过程虽谈不上呕心沥血,但也可算绞尽脑汁。在此也呼吁粉丝朋友积极参与互动,或点在看,或分享,或留言评论,当然如能买杯咖啡,那就更好啦!如果大家对此类话题感兴趣,我会写出系列信号处理文章以答谢各位的厚爱,如果大家对此类话题不感兴趣,就不在花过多时间整理发布了。在此感谢各位关注厚爱!
何为IIR滤波器?
无限冲激响应(IIR:Infinite Impulse Response)是一种适用于许多线性时不变系统的属性,这些系统的特征是具有一个冲激响应h(t),该冲激响应h(t)不会在特定点上完全变为零,而是无限期地持续。这与有限冲激响应(FIR:Finite Impulse Response)系统形成对比,在有限冲激响应(FIR)系统中,对于某个有限T,在时间t》 T时,冲激响应确实恰好变为零。线性时不变系统的常见示例是大多数电子和数字滤波器。具有此属性的系统称为IIR系统或IIR滤波器。对于什么叫冲激响应,这里就不展开解释了,有兴趣的可以查阅相关书籍。
这是常见的教科书式数学严谨定义,很多人看到这一下就蒙了,能说人话吗?
线性时不变系统理论俗称LTI系统理论,源自应用数学,直接在核磁共振频谱学、地震学、电路、信号处理和控制理论等技术领域运用。它研究的是线性、非时变系统对任意输入信号的响应。虽然这些系统的轨迹通常会随时间变化(例如声学波形)来测量和跟踪,但是应用到图像处理和场论时,LTI系统在空间维度上也有轨迹。因此,这些系统也被称为线性非时变平移,在最一般的范围理论给出此理论。在离散(即采样)系统中对应的术语是线性非时变平移系统。由电阻、电容、电感组成的电路是LTI系统的一个很好的例子。比如一个运放系统在一定频带范围内满足信号的时域叠加,输入一个100Hz和200Hz正弦信号,输出频率是这两种信号的线性叠加。
用数学对LTI系统描述:
线性:输入x1(t),产生响应 y1(t),而输入x2(t),产生相应y2(t) , 那么放缩和加和输入 ax1(t)+bx1(t), 产生放缩、加和的响应ay1(t)+by1(t),其中a和b是标量,对于任意的有:
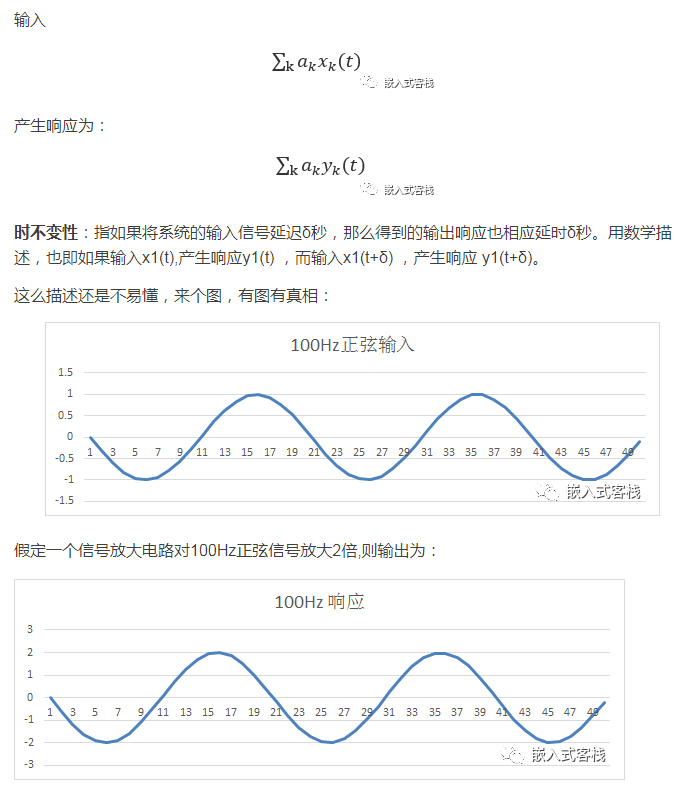
而对200Hz的正弦信号,假定其放大倍数为1.7倍。(做过运放电路设计的朋友应该有经验,在其同频带其放大倍数往往并不平坦,也即幅频响应在频带内不平坦,这是比较常见的)。也即输入为:
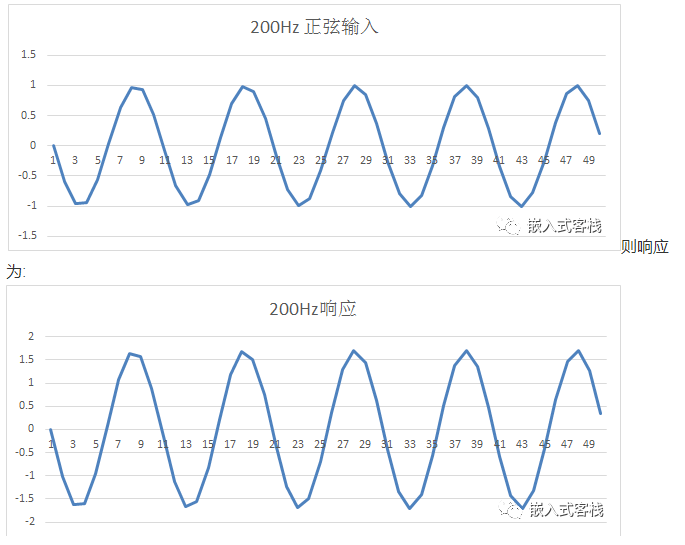
那么如果输入100Hz和200Hz的时域叠加信号,则其输入为:
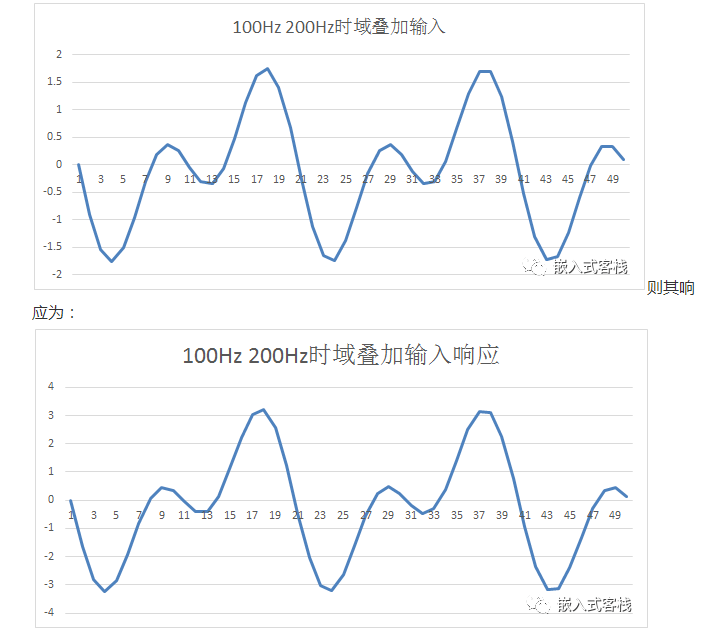
由这些图可看出,输入信号的形状保持不变,输出为对应输入的线性时域叠加。对于时不变,就不用图描述了,在一个真实电路中,如果输入延迟一定时间,则响应对应延迟相同时间输出。
上面这么多文字只是为了描述在什么场合可以使用IIR滤波器对信号进行数字滤波。总结而言,就是在线性时不变系统中适用。换言之,在大多数电路系统中我们都可以尝试采用IIR滤波器进行数字滤波。
那么究竟什么是IIR滤波器呢?从数字信号处理的书籍中我们能看到这样的Z变换信号流图:
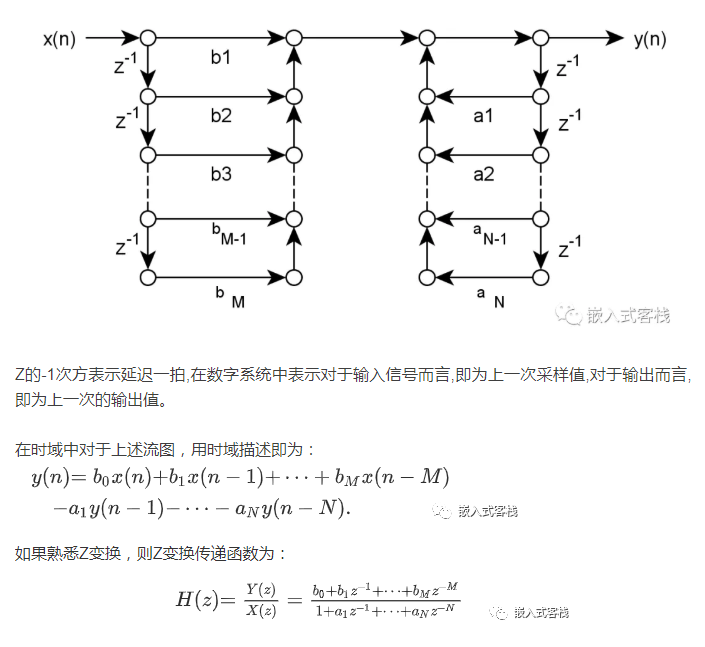
上述数字滤波器,如果从编程的角度来看,x(n-1),表示上一次的信号,可能是来自ADC的上次采样,而y(n-1)则为上一次滤波器的输出值,对应就比较好理解x(n-N)就表示前第n次输入样本信号,而y(n-M)则为前第M次滤波器的输出。
说了这么多,只是为了更好的理解概念,只有概念理解正确,才能使用正确。概念理解这对工程师而言,非常之重要。
如何设计呢?
MATLAB提供了非常容易使用的FDATool帮助我们设计数字滤波器,真正精彩的地方开始了,让我们拭目以待究竟如何一步一步设计并实施一个IIR滤波器。首先打开MATLAB,在命令行中敲fdatool,然后敲回车
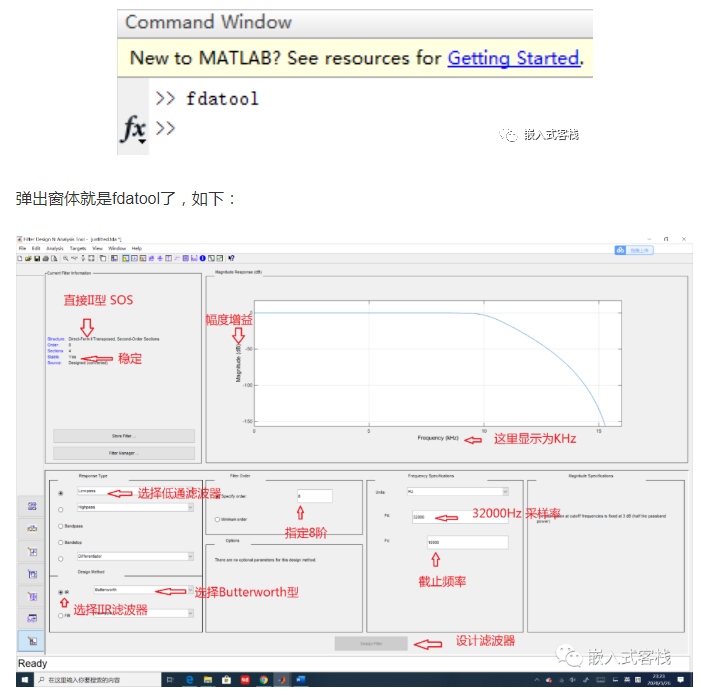
在设计具体,有几个相关概念需要澄清:Fs:采样率,单位为Hz,真实部署在系统中,请务必确保样本是按照恒定采样率进行采样,否则将得不到想要的效果。Fpass: 通频带,单位为Hz,即系统中期望通过的最高频率。Fstop: 截至频率,即幅频响应的-3dB处的频率,这个如不理解,请自行查阅相关书籍。分贝dB: 这是一个无单位反应输出与输入倍数的一个术语。电学中分贝与放大倍数的转换关系为:
A(V)(dB)=20lg(Vo/Vi);电压增益,Vo 为输出电压,Vi为输入电压
A(I)(dB)=20lg(Io/Ii);电流增益,Io 为输出电流,Ii为输入电流
A(p)(dB)=10lg(Po/Pi);功率增益,Po 为输出功率,Pi为输入功率
滤波器类型:这里有Butterworth(巴特沃斯)、Chebyshev Type I,Chebyshev Type II、(切比雪夫)、Elipic 等可选。
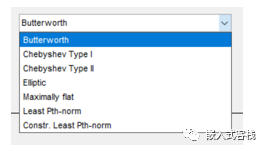
巴特沃斯 Butterworth,也被称作最大平坦滤波器。巴特沃斯滤波器的特点是通频带内的频率响应曲线最大限度平坦,没有纹波。
切比雪夫 Chebyshev,是在通带或阻带上频率响应幅度等波纹波动的滤波器。切比雪夫滤波器在过渡带比巴特沃斯滤波器的衰减快,但频率响应的幅频特性不如后者平坦。
椭圆 Elliptic,椭圆滤波器是在通带和阻带等波纹的一种滤波器。
…这里就不一一介绍了,有兴趣可以去查信号处理书籍。
就其特点,这里对其中几种略作介绍:
巴特沃斯具有最平坦的通带。
椭圆滤波器衰减最快,但是通带、阻带都有波纹。
切比雪夫滤波器衰减比巴特沃斯快,但比椭圆滤波器慢,波纹区域可选择。
假设我们需要设计一个IIR滤波器,采样率为32000Hz, 有用信号频率在10000Hz内,设计IIR滤波器对信号进行数字滤波。这里为节省算力,我们指定滤波器的阶数,也即传递函数中N/M中的最大值,一般而言N大于M。
这里指定阶数为8阶,类型指定为巴特沃斯型IIR滤波器,输入阶数8阶,采样率32000Hz,然后点击Design Filter如下图所示:
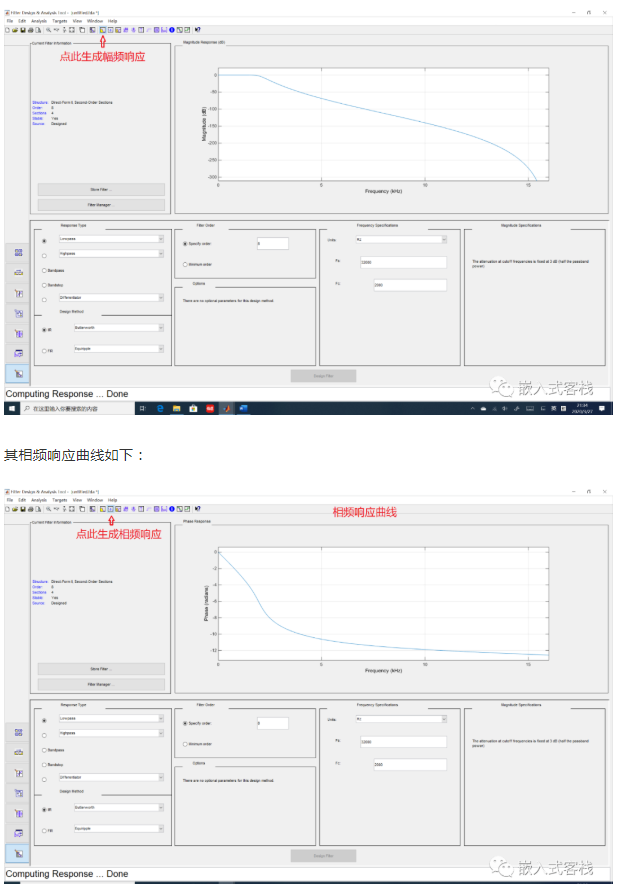
除此之外,我们还可以将幅频与相频曲线放在一个频率坐标上去看设计结果:
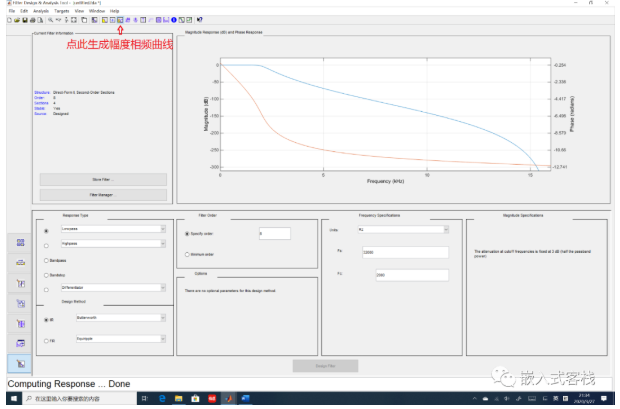
导出滤波器参数,这里我们选择,
然后就得到了一个文件,保存2KHz_LPF.fcf,文件名随你喜欢。
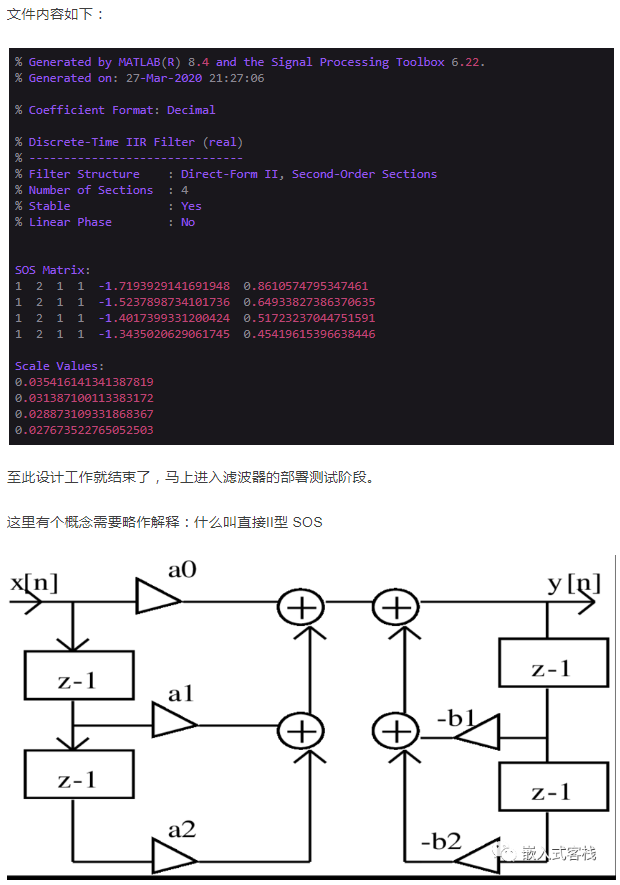
所谓直接II型,SOS(second order section)理解很简单,本质是将IIR Z传递函数分解为上述二阶块的级联形式。
部署测试滤波器
到这里,没有经验的朋友可能会说,这么一堆参数我该咋用呢?
需要自己去写前面描述的计算公式吗?当然你也可以这么做,这里就不写了,ARM的CMSIS库已经帮大家设计好了种类繁多的数字信号处理函数实现了,而且经过了测试,这里直接拿来用即可。有兴趣自己写也不难,只要理解Z传递函数概念内涵,非常容易实现。这里我们采用32位浮点实现函数:
arm_biquad_cascade_df1_f32。该函数位于:
CMSIS\DSP\Source\FilteringFunctions\arm_biquad_cascade_df1_init_f32.c
CMSIS\DSP\Source\FilteringFunctions\arm_biquad_cascade_df1_f32.c
我们来看一看这个函数:
arm_biquad_cascade_df1_init_f32.c:
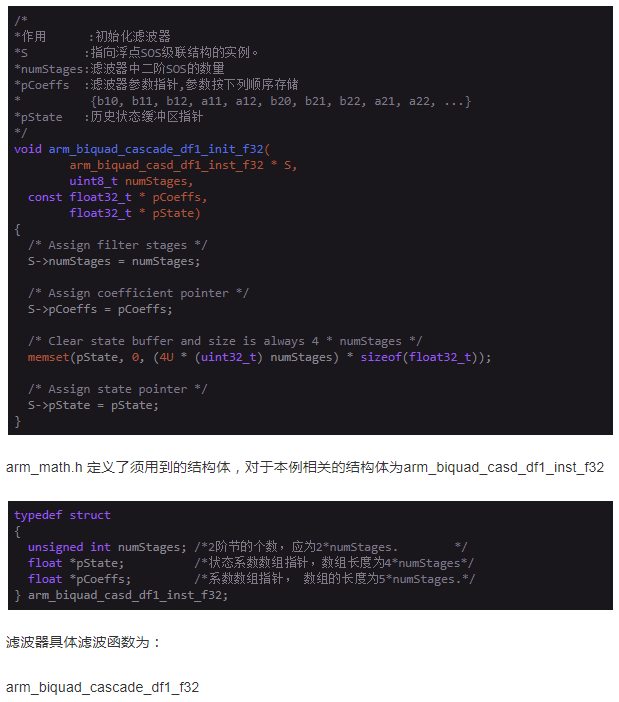
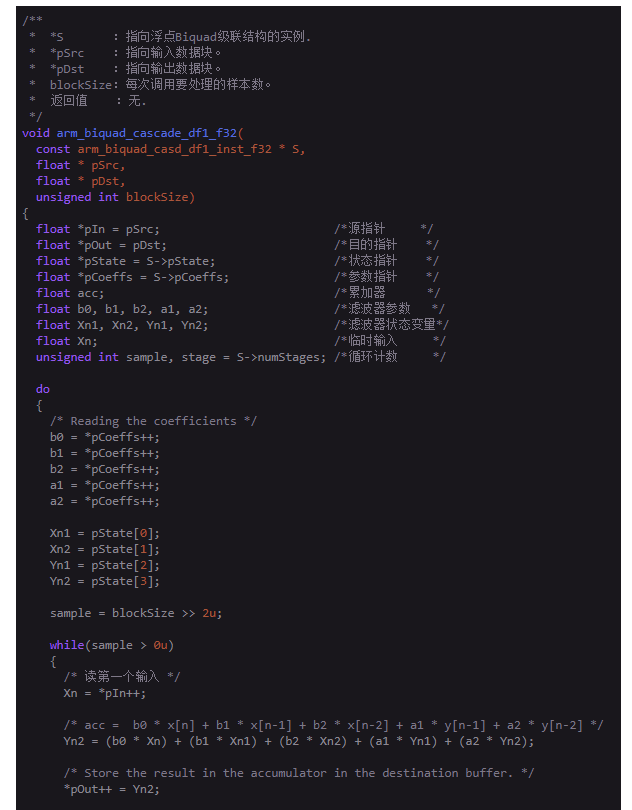
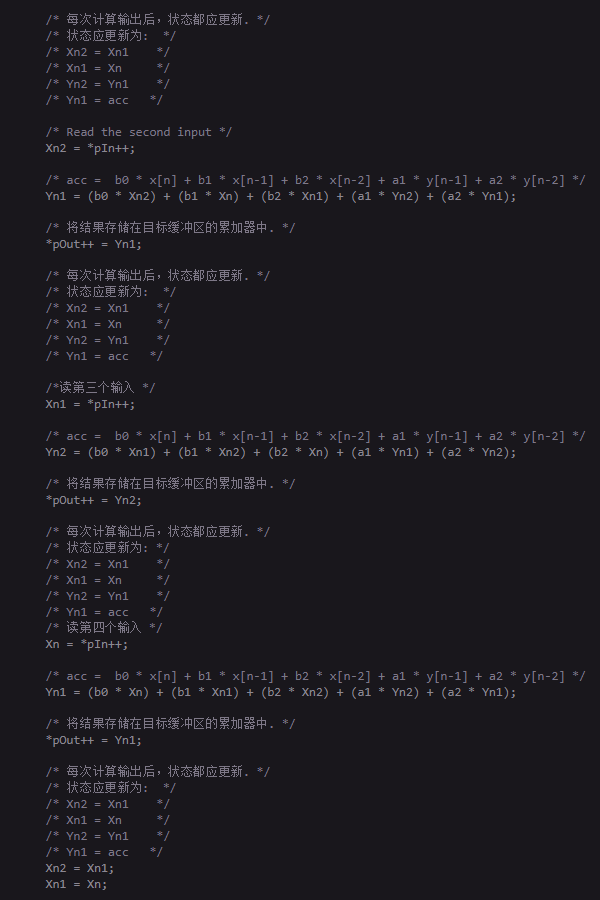
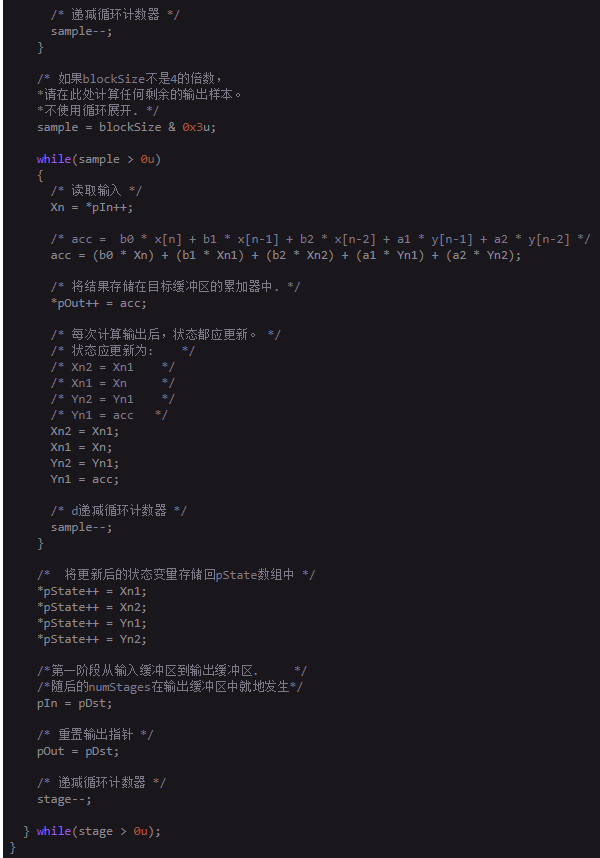
开始测试:
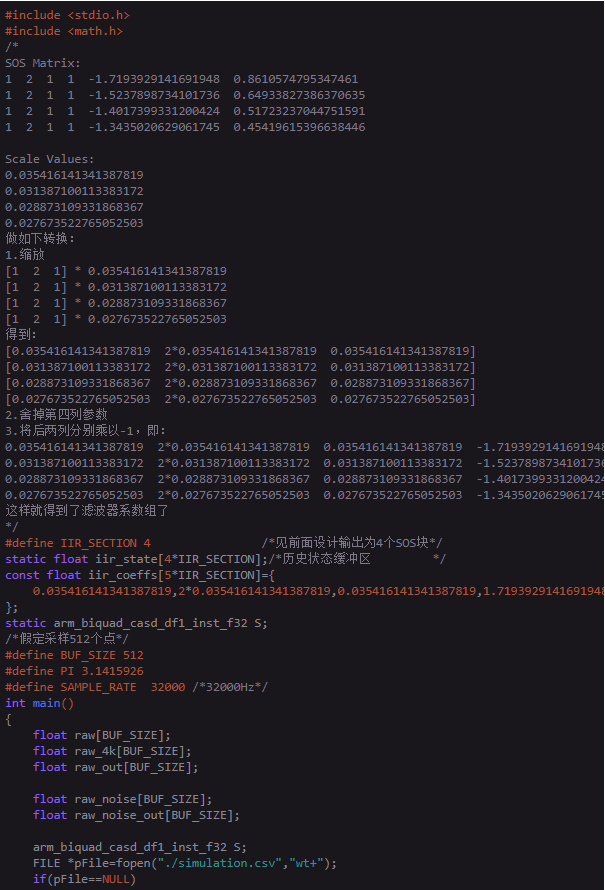
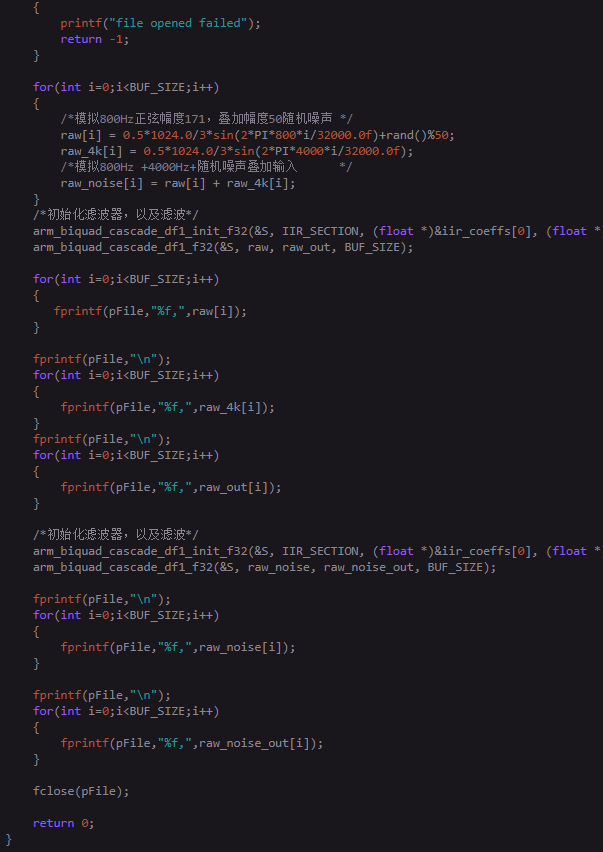
(编者注:以上是上截图不完整部分的补充:)
const float iir_coeffs[5*IIR_SECTION]={
0.035416141341387819,2*0.035416141341387819,0.035416141341387819,1.7193929141691948,-0.8610574795347461, 0.031387100113383172,2*0.031387100113383172,0.031387100113383172,1.5237898734101736,-0.64933827386370635, 0.028873109331868367,2*0.028873109331868367,0.028873109331868367,1.4017399331200424,-0.51723237044751591, 0.027673522765052503,2*0.027673522765052503,0.027673522765052503,1.3435020629061745,-0.45419615396638446
};
static arm_biquad_casd_df1_inst_f32 S;
/*假定采样512个点*/
(补充完成,接上)
利用csv文件,将模拟数据存储,直接用excel打开,将行数据生成曲线图如下:
有兴趣也可以写个界面直接显示,甚至绘制出谱线图,做进一步分析。
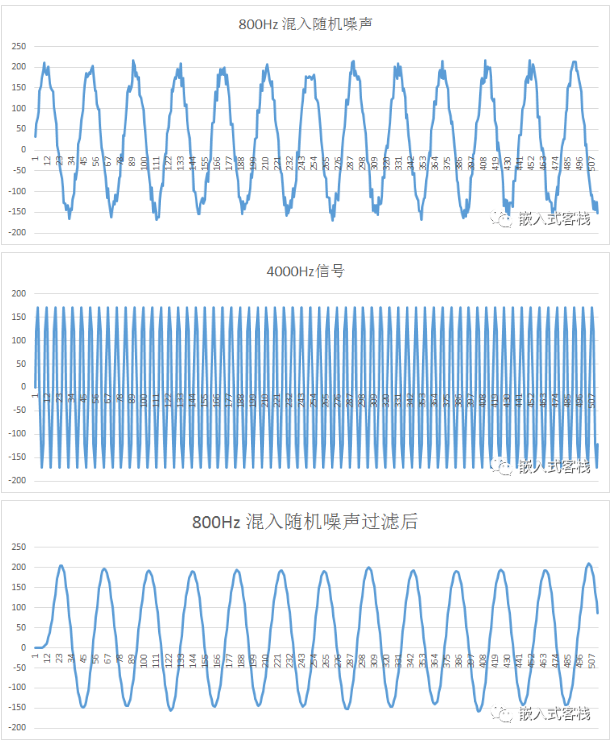
第一幅图,为800Hz信号混入随机噪声的波形
第二幅图,为4000Hz信号,对假定系统为无用干扰信号
第三幅图, 为800Hz 混入随机噪声过滤后,已经很好的还原有用信号频率
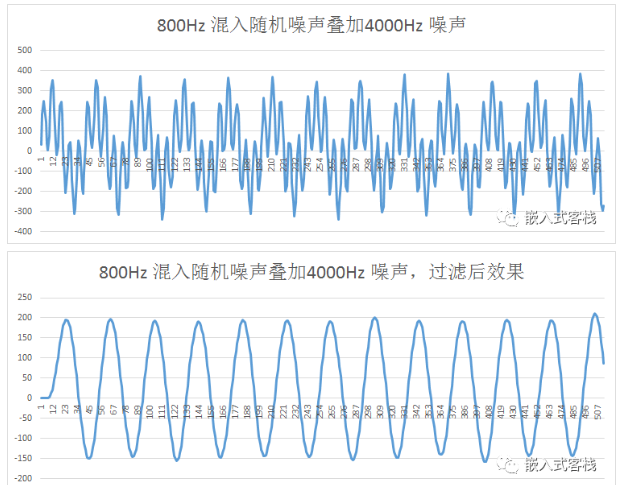
第四幅图, 为800Hz信号混入随机噪声,同时叠加4000Hz干扰的波形,对系统而言,从时域中,明显可见,有用信号已经完全扭曲
第五幅图,为800Hz信号混入随机噪声,同时叠加4000Hz干扰的输入,经过该低通滤波器后的波形,与第三幅图基本一样,已经非常好的滤除了干扰信号。
总结:
IIR滤波器在线性时不变系统中可以很好的解决工程中一般噪声问题
如果需要设计带通、高通滤波器其步骤基本类似,只是滤波器的参数以及SOS块个数可能不一样而已
需要提醒的时,IIR的相频响应不线性,如果系统对相频响应有严格要求,就需要采用其他的数字滤波器拓扑形式了
实际应用中,如果阶数不高时,现在算力强劲的单片机或者DSP以及可以直接使用浮点处理。
如果对处理速度有严格的实时要求,需要在极短时间进行滤波处理,可以考虑降低阶数,或采用定点IIR滤波算法实现。也或者将文中函数进行汇编级优化。
欢迎大家进行留言讨论。
-
IIR数字滤波器时域滤波效果2023-11-18 526
-
FIR数字滤波器设计2022-04-05 6519
-
用matlab生成IIR数字滤波器系数2021-08-17 1680
-
怎么实现基于Matlab的IIR数字滤波器设计?2021-05-31 1702
-
请问如何去设计IIR数字滤波器?2021-04-14 1908
-
如何使用FPGA实现IIR数字滤波器的设计2020-08-06 1192
-
基于FPGA和MATLAB实现IIR数字滤波器的设计和仿真验证分析2020-07-23 3610
-
IIR数字滤波器的FPGA实现2018-03-02 1097
-
DSP04_IIR_数字滤波器设计和实现2016-07-29 1098
-
基于LabVIEW平台的IIR数字滤波器设计2016-01-20 913
-
IIR数字滤波器设计2015-12-25 997
-
IIR数字滤波器的设计2009-05-10 2596
-
IIR数字滤波器设计-在FPGA上实现任意阶IIR数字滤波器2008-01-16 2856
全部0条评论

快来发表一下你的评论吧 !

