

作为测试过程的频率响应方法及在液压伺服系统中的应用
电子说
描述
频率响应是指以正弦波作为命令输入来绘制机器或过程输出的动态响应。测试设备可用于测试物理系统,并且存在允许使用完全理论方法的分析技术和工具。在这里,我们将简要介绍一下作为测试过程的频率响应方法,并总结系统设计师可以从这些过程和结果中获得什么。
如果可以用正弦测试信号激励设备并测量其输出,则频率响应测试方法可以应用于任何事物。在电液运动控制中,制造商为伺服和比例阀发布的数据中最常遇到频率响应。实际上,我之所以主张使用伺服阀和比例阀(而不是其他类型的阀)的一个令人信服的原因是,因为伺服阀和比例阀存在太多的频率响应数据,而其他设备几乎没有。有了这些信息,我们就可以在构建系统之前更好地预测系统的性能。
频率响应测试非常简单,观察几分钟后即可轻松理解。这与在纯学术环境中学习数月相反。这是一种用于测量元件(例如阀)动态响应的方法。
另一种流行的动态测试程序是测量对阶跃输入的输出响应。频率响应和阶跃响应是相关的,因为它们来自同一系统。但是,频率响应方法比阶跃响应更可靠,因为在使用频率响应分析仪时,在频率响应测试中固有地抑制了失真和噪声。
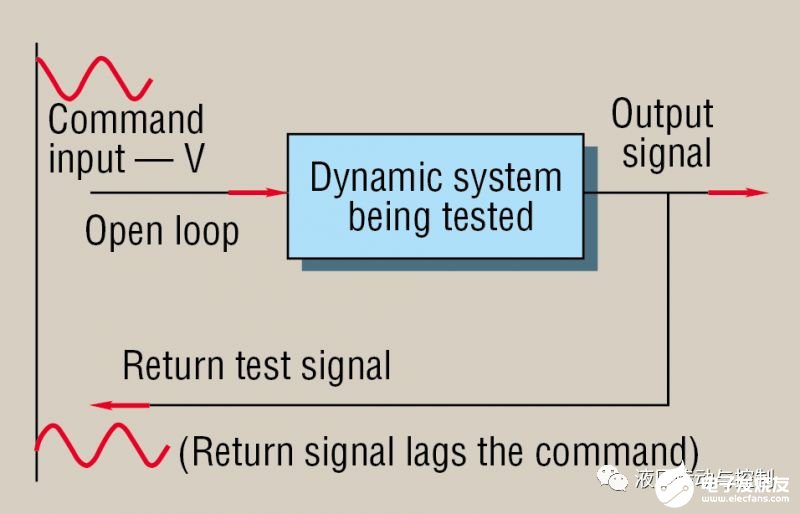
图1.图显示了频率响应测试环路的框图。频率响应可用作动态测试,因为当与频率响应分析仪结合使用时,它固有地抑制了失真和噪声。
如图1所示,该测试涉及对输入施加受控幅度的正弦波形,从而使被测设备(例如阀)来回循环。同时,输出也将以相同的频率循环。但是,输出和指令输入的幅值不一定与指令输入相同。就阀门而言,输入(电流)和输出(流量)甚至不在相同的度量单位中。此外,在大多数实际物理动态过程中,输出将经历相位滞后。即,输出必须一定落后于输入。测试操作员记录频率,输出幅值以及输入和输出之间的相位滞后量(以度为单位)。
接下来,增加频率,同时将输入正弦波保持在恒定的峰-峰值幅值。通常以度为单位绘制相位,并通过以下等式以分贝(dB)给出幅值:
A = 20 log | On÷Ol |
其中
A:阀频率响应的幅值
On:是任意频率的输出,并且
Ol:是最低频率的输出。因此,我们看到,对于最低的测试频率,伺服阀的频率响应测试数据始终从0 dB开始。
在较高的测试频率下,通常会出现较高的相位滞后,并且输出幅值会发生变化。在任何类型的机器上,随着频率的增加,输出幅值将无法跟上输入幅值,这是正常现象。也就是说,总会有一些频率的输入命令振动得如此之快,以至于输出根本无法跟上。因此,输出幅值趋于随频率增加而减小,并且输入与输出之间的相位滞后趋于增大。
也有例外。当被测系统中存在共振时,在某些狭窄的频带或范围内,输出幅值会随频率增加。当存储在弹簧或其他挠性构件中的势能与运动质量的动能交换时,就会发生共振。当质量的动能与内部压缩流体中存储的势能相互作用时,会在液压系统中产生共振。
当发生共振时,有时会随着输出振幅的增加而显示出共振,从而增加频率。图2中所示的伺服阀频率响应数据就是这种情况。在30 Hz时,比0 dB参考值高出约0.8 dB。共振上升的存在表明阀有弹性的趋势,如果使用阶跃输入进行测试,则阀的输出将趋向于在该频率附近“响”。上升表明阀的设计者将其响应调整为阻尼不足。大多数伺服阀已调整为无共振上升。但是,也有一些例外。阻尼不足的特性伴随着共振上升。描述这种情况的一种方法是,“欠阻尼意味着存在过冲和共振上升”。
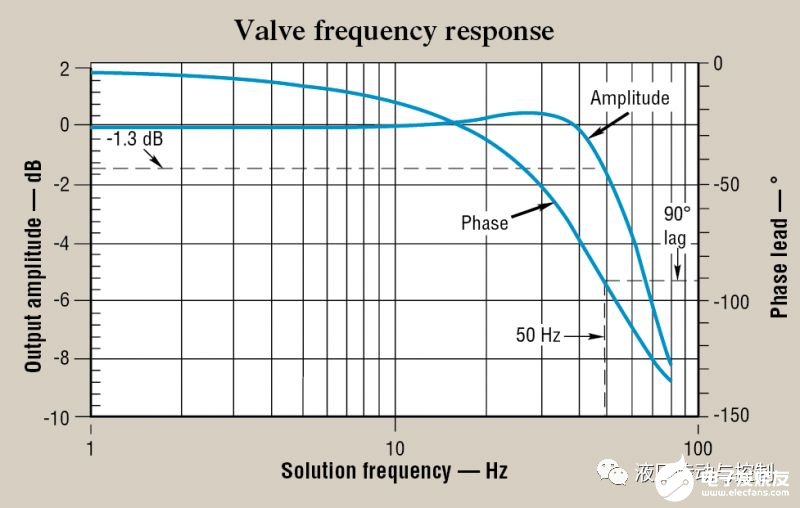
图2.伺服阀频率响应数据显示了当质量的动能与压缩流体中存储的势能相互作用时,液压系统中如何发生共振。振幅在30 Hz左右的升高表明存在共振,并且该阀设计为具有稍微欠阻尼的响应。
图2中的频率响应图至少是许多伺服阀的典型特性,可以用来比较一个阀与另一个阀的响应。任何阀的重要“基准”频率是相位滞后达到90°的频率。请注意,在参考阀中,频率约为50 Hz。显然,如果有另一个阀门的90°相位滞后频率高于50 Hz,则该阀门的响应速度将比图2中所示的更快。
将一个阀与另一个阀进行比较时,应始终使用90°相位滞后频率。该频率称为阀频率,阀频率响应或阀带宽。所有术语或多或少都是同义词。无论如何,该频率有助于预测阀响应与应用系统所需性能之间的匹配程度。一些设计人员使用-3dB的频率。但是,作为比较基准,这是不可靠的。在评估阀门与最终系统中其余部件的配合情况时,它也没有价值。90°相位滞后频率的最重要特征是,它使我们能够将阀频率与液压机械共振频率进行比较,液压共振频率是由于流体的可压缩性(液压电容或柔量)与执行器负载质量相互作用而产生的共振。
一些背景
在奈奎斯特(Nyquist)的开创性论文中,他将正弦分析的思想应用到了动态系统中,但是在当时非常受其它影响的情况下,他以非常神秘的数学术语将其应用。九年后,Bode发表了同样重要的论文。他教我们,通过以分贝表示正弦频率响应的幅值,将一个设备(例如阀)的幅值和相位响应与另一设备(例如负载和执行器子系统)的幅值和相位响应相加就变得很简单。在那时,当选择计算辅助成为计算规则时,确实如此受欢迎。尽管计算机发生了革命性的变化,并且计算机执行复杂的计算非常容易,但是众所周知的Bode图仍然是系统设计人员最喜欢的工具。
Bode和Nyquist(都是贝尔实验室的研究工程师)对确定为什么某些音频放大器会突然振荡而另一些音频放大器不会突然振荡的想法很感兴趣。如今,运动控制和反馈控制系统的设计人员仍在为机器的振动问题而苦苦挣扎。如果继续下去,这种振荡可能是自毁的。频率响应方法使我们能够合理估计将产生稳定的,无振荡的伺服机构的电子调谐极限。
博德的方法要求我们测试和研究开环系统,然后使用分析技术询问“假如是”闭环会如何。例如,可以在开环配置中测试完整的位置伺服机构(图3),以找到使系统不稳定的必要条件。请注意,我们不是使用正弦测试数据(频率响应特性)来确定系统在正弦输入下的性能,而是在系统振荡之前可以获得多少伺服环路增益。这就是频率响应方法的精妙之处。
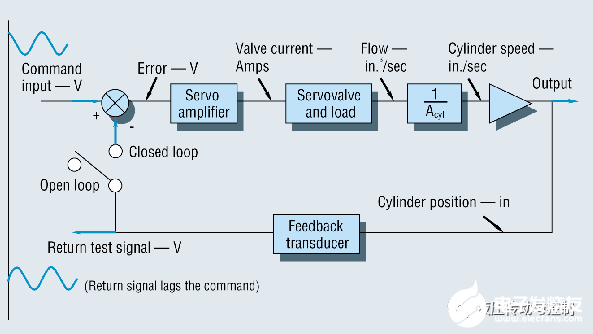
图3.左侧的开关允许在开环配置下测试该闭环电液系统,以确定引起不稳定的频率响应特性。然后,该系统可以以减少到引起振荡的增益的一半左右的增益进行操作。
为了说明这一点,请考虑图3的系统。它将首先在开环位置使用反馈开关进行测试。随着频率的增加,我们寻找在指令输入和开环反馈信号之间造成180°相位滞后的任何频率。(在水力机械系统中,基本上可以确定存在此频率。)在该频率下,如果输出(开环反馈信号)的幅值等于或大于输入命令幅值,则可以闭合反馈开关。然后,通过负反馈过程,该180°相位移将经另一个180°相位。结果是可以消除正弦指令输入激励,并且闭环系统将处于持续振荡状态。这是一个不稳定的系统,如果无法停止振荡,则是不切实际的。减小伺服环路增益是停止振荡的正常过程。这是通过更改伺服放大器的增益设置来实现的。
上一段以非数学的形式提出了伺服回路稳定性的经典标准。通过更改对180°相位频率的搜索,可以简化一点。考虑以下情况:假设在搜索中找到了临界的180°相位频率,但是开环反馈信号的幅值小于命令输入幅值。该频率下的开环增益小于1,在分贝标度上小于零。
现在我们问自己:“如何增加增益,使反馈信号幅值等于指令信号幅值(伺服环路增益为零dB)?”我们只需要增加伺服放大器的增益,系统就会陷入振荡。因此,只要有180°的相位频率,只要增加伺服放大器的增益即可实现持续振荡。每个电液系统都存在一个180°的相位频率,因此我们始终可以将这种系统调整到不稳定的程度。
当然,我们不希望系统振荡。调整到不稳定点的目的是找到将产生不稳定的最终增益。然后将增益减小到引起稳定振荡的值的一半左右,并留在那里。增益降低50%大约等于5 dB的增益裕度。即,将增益设置为低于不稳定点5 dB。对于许多电动液压运动控制系统而言,这已足够。在设计过程中使用频率响应方法,我们可以预测不稳定性的增益。因此,我们可以从不稳定性中估计出伺服系统中预期的误差。
共振频率和阀频率
流体力学共振频率(HMRF)与流体体积和负载质量成反比:受压流体体积越大,负载质量越大,HMRF越低。HMRF越低,实现伺服系统的快速响应控制就越困难。相反,系统变得缓慢而富有弹性。确实,有些人将流体的可压缩性等同于弹簧。这个比喻有一定的价值。
当HMRF太低时,这种弹性可能是系统的瓶颈。我见过HMRF低至0.5 Hz,高至700Hz以及介于两者之间的所有值的系统。HMRF低是大负载质量连接到小油缸的特征。增加油缸面积始终具有提高HMRF的作用。当HMRF小于阀的频率时,它将成为系统的瓶颈。阀频率fv是根据阀门制造商发布的频率响应测试数据产生90°相位滞后的频率。
现在,我们有了将一种频率与另一种频率进行比较的直接基础,这使我们能够得出重要的结论。的确,当小于阀频率时,HMRF会限制系统响应。但是,当阀的频率小于HMRF时,阀将成为限制装置。规则很简单:动态瓶颈是fv和fn中的较小者。
通常,当系统的HMRF小于其阀频率时,很难设计出具有清晰响应的系统。不幸的是,系统的HMRF通常低于其阀频率。因此,这意味着HMRF通常是主要的,这代表了最具挑战性的设计方案。换句话说,最坏的情况是最常见的情况。
此外,当阀频率约为HMRF的两倍时,提高阀频率对系统性能的影响可忽略不计,因为性能将几乎完全受到HMRF的影响。应该清楚的是,闭环带宽必须始终小于fv和fn中的较小者。唯一剩下的问题是:少多少?
闭环带宽的限制
最大闭环带宽(频率响应)必须小于一个称为分离比的值,该值始终小于1。用数学术语来说:
fmax 《 ps ×(lesser of fv or fn)(fv 或fn中的较小者),
其中
fmax 是最大系统关闭带宽
ps 是分离率,并且
fv 和 fn是阀和油缸负载共振频率,单位为Hz。
当HMRF占主导地位(《fv)时,分离比完全由液压机械系统的阻尼比控制:
ps =2Zn
其中
Zn是阻尼比,是振动减弱趋势的度量。
造成阻尼的因素有两个:从执行器一侧到另一侧的内部泄漏(无论是从执行器内部还是从控制阀内部泄漏)和摩擦(是否来自执行器或其负载)。由于制造商努力减少内部泄漏和摩擦,因此大多数液压机械系统的阻尼度可能会非常低,这不足为奇。实际上,当负载可以以可忽略的摩擦力移动时(如由循环线性球轴承支撑时),阻尼比可能低至0.03或0.05。诚然,系统摩擦和阻尼比是要在系统中评估的最难以捉摸的量。但是,它们与频率一起绝对控制着系统的性能极限。
计算示例
考虑一个示例来演示此讨论。假设已计算出系统的油缸机械共振频率,发现其为18 Hz。进一步假设其伺服阀的90°相位滞后频率为65 Hz,并且由于摩擦和内部阀门泄漏,我们估计液压机械阻尼比约为0.05。我们可以计算出最大可能的闭环系统带宽:
fmax 《 ps x( fv 或 fn的小者)
fmax 《2 x 0.05 x 18
fmax 《1.8 Hz
最大闭环带宽fmax 只有1.8 Hz,仅为HMRF的十分之一!在启动时,我们通过增加伺服放大器增益来增加系统带宽。如果我们增加增益直到带宽达到1.8 Hz,然后再尝试进一步增加,则伺服回路将陷入持续的振荡状态,从而变得毫无价值。必须降低增益以重新建立稳定性。
系统带宽之所以重要,是因为它与定位精度(或更准确地说,是定位误差和跟随误差)之间存在直接的反比关系。已经表明:
∆xp = (∆IT × Gsp)/(2’ fsys)
其中
∆xp 是预期的稳态定位误差(in。)
∆IT 是由八种已知的外部干扰引起的总预期阀电流变化(安培),
Gsp是最高预期速度和负载下的速度增益[(in.x A)/秒],并且
fsys是实际的闭环系统带宽(Hz)。
输出位置永远不会是我们想要的位置-只能关闭。电液位置伺服机构中存在八种导致定位不完善的已知干扰:
• 阀温度变化
• 供油压力变化
• 回油箱油口压力变化
• 分离摩擦
• 负载变化
• 阀滞环
• 阀阈值,以及
• 阀死区。
所有这些必须分解为等效的阀电流,然后加在一起得出总的预期阀电流,即IT增量。总的来说,评估给定系统的这八个“错误贡献者”不仅仅是一个琐碎的过程。但是,经验告诉我们,对于具有“典型”伺服阀性能的零遮盖阀,∆IT 约为阀额定电流的2%或3%。如果阀是成比例的并且具有实质性的遮盖,则我们通常仅使用遮盖而忽略其他七个贡献者。
从技术上讲,对于最坏的负载条件,必须使用所选控制阀的特性来计算速度增益。如果设计人员采用良好的工程实践来选择控制阀(如果选择该阀以在最坏的负载和速度组合下提供最大的功率传递),那么速度增益Gsp将等于目标设计执行器速度除以约为阀额定电流的2/3。有了这些信息,我们现在可以估计预期的系统“准确性”。
假设我们正在设计的系统在最坏情况下必须使用基本上为零遮盖的伺服阀以21in./sec的速度推动负载。可以首先计算该页面左上部分的分子:
∆IT × Gsp = (0.02 × IR x 21) ÷ (0.67× IR),
其中
IR是阀的额定电流,可以从公式中抵消。
现在
∆IT Gsp=(0.02×21)×0.67
∆IT Gsp = 0.63英寸/秒
如果我们假设伺服回路已经在不稳定性发生之前调整到允许的最大值,则fsys设置为fmax,因此可以估算误差:
∆xp = ∆IT Gsp÷2 ’ fsys
但是由于分子已经被求值:
∆xp = 0.63÷(2′×1.8),
∆xp=±0.055 in
这样,我们可以预期该系统的长期定位能力约为0.055 in。
责任编辑:gt
-
伺服系统在CNC机床中的应用2024-12-10 1523
-
如何由系统函数求频率响应2024-10-18 4607
-
频率响应的基本概念与测量方法2024-07-29 11152
-
机电伺服系统有哪些_机电伺服系统工作原理2023-03-07 2656
-
针对C2000系列处理器的软件频率响应分析器工具2021-04-22 1047
-
液压伺服系统有几种类型_液压伺服系统的应用2021-02-19 5965
-
由单片机和DDS设计的频率响应测试仪2018-10-26 3646
-
液压伺服系统的组成_液压伺服系统的优缺点2018-06-04 13042
-
音响频率响应多少好_频率响应大好还是小好2018-03-19 76036
-
频率响应是什么意思_频率响应特性2017-10-31 29673
-
模糊控制及其在液压伺服系统中的应用_余兵2017-02-07 827
-
分析稳定系统中的惯性MEMS的频率响应2016-01-07 794
-
液压伺服系统的工作特性及原理2012-02-09 8875
-
连续时间LTI系统的频率响应.ppt2009-09-16 1186
全部0条评论

快来发表一下你的评论吧 !

