利用模糊CMAC神经网络优化机械臂系统中控制器的设计

1、模糊CMAC神经网络的结构和学习算法

图1显示了模糊CMAC神经网络的结构和运算过程。模糊CMAC神经网络可以用于近似一个非线性映射y（x）：Xn→Ym，其中Xn∈Rn是在n维输入空间中的应用，Ym“∈Rm是在m维输出空间中的应用［1，2］。模糊CMAC算法由决定一个复杂函数值的两个初等函数组成，如图1所示。

其中，X为连续n维输入空间；A为NA维联合空间；Y为m维输出空间。

函数φ=R（x）通过模糊量化把输入空间中的每一个点映射到联合空间A。函数P（φ）通过把由R（x）决定的联合向量映射到如下的一个可以调节加权的向量来计算一个输出y∈Y。

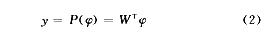
2、基于模糊CMAC神经网络的机械臂最优控制

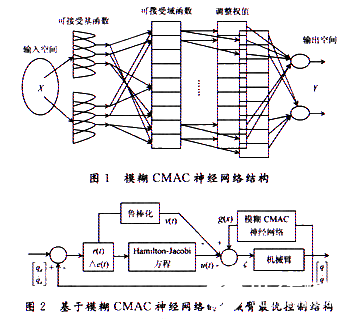
图2给出了基于模糊CMAC神经网络的机械臂最优控制结构图。机械臂关节处的外部控制转矩由最优反馈控制率和模糊CMAC神经网络输出部分组成。

三连杆机械臂的Lagrange动力学方程为：

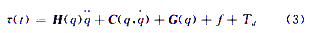
其中，q为关节转角；H（q）为惯量矩阵；C（q，q）为向心力；G（q）为重力项；f和Td分别为摩擦力项和扰动项；τ（t）为外部控制转矩。

把外部转矩定义为：

其中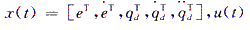，是由最优控制规律得出的控制量，g（x）是模糊CMAC神经网络的输出值。

设给定一个理想的轨迹qd（t）跟踪误差为：

定义：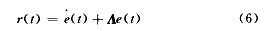

其中，Λ是恒增益矩阵或者鉴定器。

对于最优化的转矩控制器没，定义速度误差动态特性为：

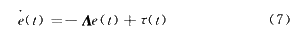
得到如下增广系统：

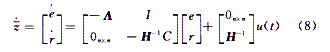
令二次性能指标：

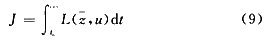
其中：

根据Hamilton-Jacobi最优化方法，可知必须存在一个函数V=V（z，t）使最优化控制u*t满足H-J-B方程［4］。

可以求得最优化控制u*t：

非线性函数通过模糊CMAC神经网络来表达。得到：

其中，WT为理想权值，εM为极大误差。

将g（x）的函数估计g（x）由模糊CMAC神经网络的输出确定，误差部分通过鲁棒化向量ν（t）来进行补偿，从而提高系统的动态特性。

权值误差估计是W=W－W，采用Lyapunov稳定性理论调节权值［6］。

取Lyapunov函数为：

其中K是正定且对称的，F=FT》On×n

基于李雅普诺夫第二法可知，如果使Lyapunov函数的时间导数L《0，则系统是渐进稳定的。也即通过调节神经网络权值矩阵，误差e可以任意小。

利用最优化反馈控制律和系统的状态空间表达式，得到神经网络的权值自适应学习规则为：

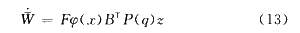
3、仿真实验

以三关节机械臂为控制对象进行仿真实验以验证所提模糊CMAC最优控制器用于机器人轨迹跟踪控制的有效性。期望的运动轨迹为：

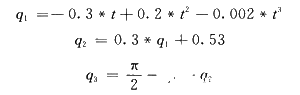
初始条件为q1（0）=0 rad，q2（0）=0．5 rad，q3（0）=1．07 rad，q1（O）=q2（0）=q3（0）=0 rad／s。采样周期为0．002 s。

CMAC中联想强度的初值取［－1，1］之间的随机值。隶属度函数取Gaussian函数，图3和图4分别给出了各关节的轨迹跟踪曲线和跟踪误差曲线。

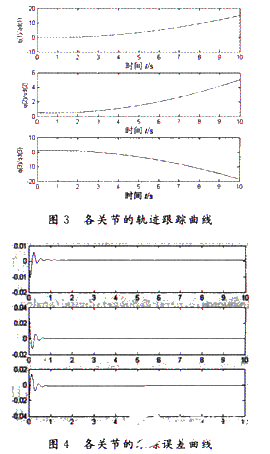
仿真结果清楚表明了模糊CMAC神经网络最优控制器克服结构和非结构不确定性的能力，同时也表明了提出的神经自适应学习算法可以改进系统动态性能的鲁棒性和适应性。

4、结 语

本文将Hkamilton－Jacobi－Bellman最优控制和CMAC神经网络结合起来，给出了一种三连杆机械臂系统的最优控制器设计方法。仿真结果证明，这种控制方法能够很好地克服机械臂系统的非线性和不确定性，实现对期望轨迹的跟踪。

责任编辑：gt