利用Visual C++6.0实现对海底大地电磁探测数据进行畸变校正处理

三维图形变换 在海底大地电磁探测技术中，传感器系统的方位及水平状态直接影响着大地电磁场分量的观测结果。因此，在观测的过程中，必须随时准确地测定系统分布的方位角和水平分量传感器的水平状态，以便对观测的数据进行方位畸变校正。另外，当测量电磁场分量的传感器系统放入海底时，由于海水的各种各样的运动，传感器系统在正常工作的同时，会产生振动，造成电场分量和磁场分量的测量数据不精确。因此要设法对测量的数据进行校正。设计上，传感器系统的振动对电场分量数据的影响是很小的，这种影响常常被忽略；但是这些振动对磁场分量数据的影响是很大的，必须进行正确的振动畸变校正，才能得到准确的磁场分量数据。

1 、方位校正原理

对于方位角和倾角所引起的干扰，校正依据的是“图形的几何变换”原理。电场只有两具分量，可以依据“二维图形的几何变换”原理。 二维图形变换的一般公式为：

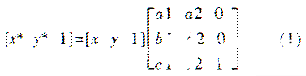
其中

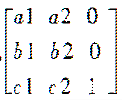
为二维变换矩阵。 三维图形变换的一般公式为：

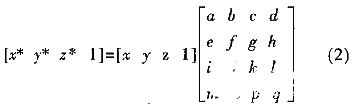
其中

为三维变换矩阵。 在海底大地电磁探测技术中，由于在海底大地测量系统中的5个探头满足右手坐标系原理，因而可以利用实验测得的电场和磁场的5个分量以及所测的倾角和对于北向的方位角进行方位和水平校正。基本坐标系如图1所示。 设在海底测得的电场和磁场的5个分量分别用Ex、Ey、Hx、Hy、Hz表示，设探头测得的X分量对于北向的夹角为α，对于立不的倾角为xt，设探头测得的Y分量对于水平面的倾角为yt，设校正后的5个分量分别为Ex“、Ey”、Hx“、Hy”、Hz“，则有：

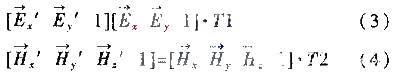
其中，T1为电场的变换矩阵，

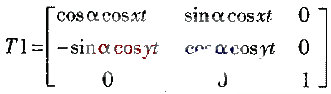
T2为磁场的变换矩阵，

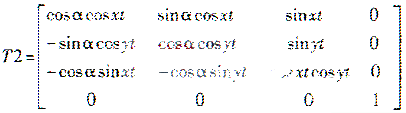
将T1和T2分别代入上式后，可以求出校正后的Ex”、Ey“、Hx”、Hy“、Hz”，即校正后电磁场分量的值。

2 、振动校正原理

对于探头振动所引起的干扰磁场，可以通过先求出探头振动所引起的干扰磁场，然后再滤波的办法进行校正。 在大地的某一点上的电场强度E为大地电场在这一点上的值E0与二次电场Es的叠加，即：E=E0+Es。在大地的某一点上的磁场强度B为大地磁场B0与二次磁场Bs的叠加，即：B=B0+Bs。 实际测量的是电场的水平方向上的两个分量，即Ex和Ey。

由于二次场Es的存在，则有： Ex=Ex“+Esx，Ey=Ey”+Esy 其中，Es为由于长探头振动所产生的二次电场（Es=Esx+Esy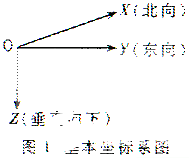）。探头的振动是不规则的，但可以将其分为两部分： （1）长探头在垂直于磁场的方向上运动，切割磁力线，产生的感生电动势为Es1（实际中，由于探头很长，达到5m左右，因此，又可以将其视为长螺线管）。 （2）探头以某一角速度旋转，造成穿过探头线圈的磁通量发生变化，所产生的感生电动势为Es2。

由于探头在海底放置，因此其旋转的角速度很小，由此造成的Es2可以忽略不计。而Es1=BLVsinβ，B、L、V为已知量。其中，B即为测量点的大地磁场B0和二次磁场Bs的叠加，由于Bs相对于地磁场来说很小，可以忽略不计，所以B≈B0；L即为探头的长度；V为探头切割磁力线的速度，由于采样时间间隔Δt很小，则第n个采样点处的探头的运动速度Vn=Vn-1+αn-1Δt（αn-1为第n-1个采样点振动传感器得的加速度，Vn和Vn-1分别为第n和n-1个采样点的速度，V0=0，Δt为采样时间间隔）；β为探头和B正向的夹角。因此，可以求出在某一点的感生电动势Es。由于此感生电动势的影响，会在长探头附近产生感应磁场Bs（二次磁场）。根据安培环路定律得：Bs=μnI（μ为探头内的磁介质的磁导率，n为探头每单位长度上线圈的匝数，I为感生电动势Es产生的电流，I=Es/R，R为探头的电阻）

。 因此：Bs=μnI =μnEs/R =μnBLVsinβ/R （5） 设第n个采样点处的感应磁志Bs和Bsn，则有： Bsn=μnBsn-1（Vn-1+αn-1Δt）sinβ/R 即：Bsn=KBsn-1（Vn-1+αn-1Δt） （6）

3 、校正结果

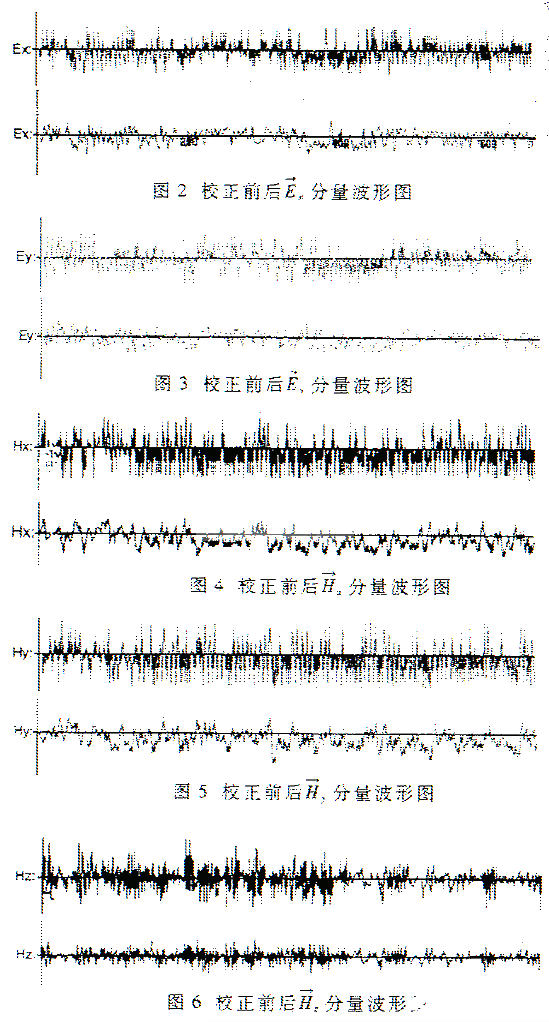
利用Visual C++6.0设计了程序，对探测数据进行了畸变校正处理，取得了较好的效果。 对实际测得的数据进行了多次处理，现先取一些典型的实际结果做一些说明，以给读者一个直观的理解。图2～图6是传感器系统在某一点测得的校正前后的电磁场分量的波形图。

研究结果表明，在观测过程中，一定要保证随时准确地测定系统分布的方位角和水平分量传感器的水平，以便对观测数据进行正确的方位校正。 只要知道探头的一些参数和各采样点的振动传感器所测得的加速度的值，就可以求出在第n个采样点的干扰成场的大小，从而可以校正由于海水运行引起的传感器探头振动所带来的电磁场的干扰，就可以得到校正后的电磁场的真实值。校正处理结果证实了振动校正的正确性。从校正前后的波形图上看，校正算法对高频电磁干扰的抑制效果明显。

责任编辑：gt