采用极点配置法实现倒立摆系统的设计

1 引言

倒立摆是研究控制理论的典型实验平台。由于倒立摆系统本身所具有的高阶次、不稳定、多变量、非线性和强耦合特性，许多现代控制理论的研究人员一直将它视为典型的研究对象，不断从中发掘出新的控制策略和控制方法。控制器的设计是倒立摆系统的核心内容，因为倒立摆是一个绝对不稳定的系统，为使其保持稳定，并且可以承受一定的干扰，采用极点配置法设计用于直线型一级倒立摆系统的控制器。

2 数学模型的建立

因为倒立摆系统本身是一个自不稳定的系统，因此实验建模存在一定的困难。然而，经过谨慎的假设，忽略掉一些次要因素，就能使倒立摆系统成为一个典型的运动的刚体系统，使之在惯性坐标系内应用经典力学理论就能建立系统的动力学方程。下面采用牛顿一欧拉方法建立直线型一级倒立摆系统的数学模型。

2．1 微分方程的推导

在忽略空气阻力和各种摩擦后，可将直线一级倒立摆系统抽象成小车和匀质杆组成的系统，如图l所示。

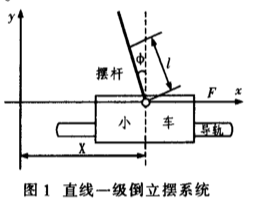
假设M为小车质量；m为摆杆质量；b为小车摩擦系数；

l为摆杆转动轴心到杆质心的长度；I为摆杆惯量：F为加在小车上的力；x为小车位置；φ为摆杆与垂直向上方向的夹角；

θ摆杆与垂直向下方向的夹角图2示出系统中小车和摆杆的受力分析图。其中，N和P为小车与摆杆相互作用力的水平和垂直方向分量脚。值得注意的是：在实际倒立摆系统中检测和执行装置的正负方向已确定，因而矢量方向定义如图2所示，图示方向为矢量正方向。

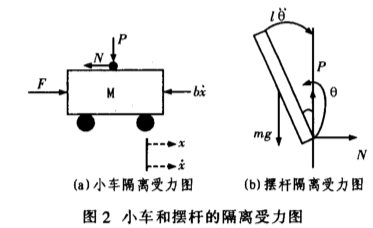
分析小车水平方向所受的合力，可得方程为：

MX=F—bi—N

由摆杆水平方向的受力进行分析，可得：

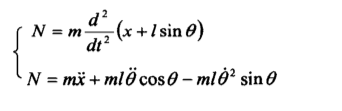
2．2 状态空间方程

由方程组（8）对x，φ解代数方程，整理后得：

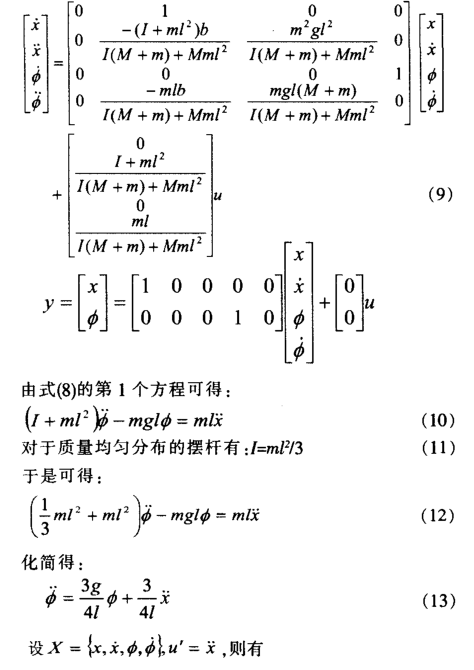
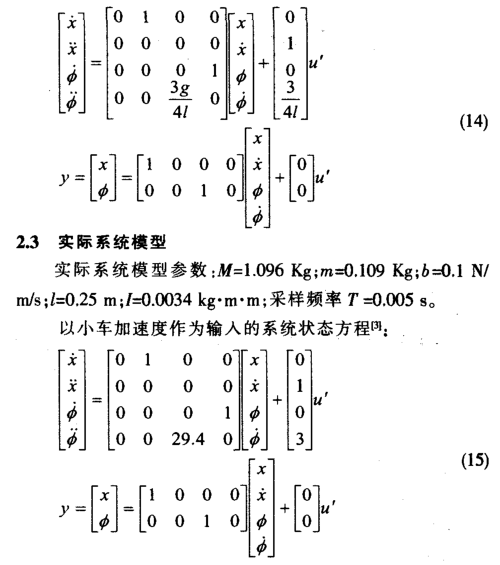
3、 状态空间极点配置

4 、仿真验证

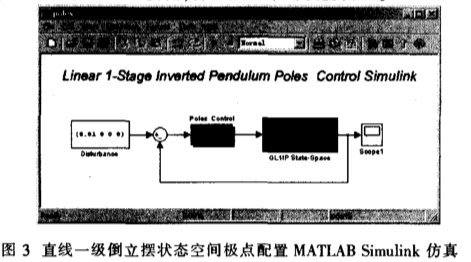
建立直线一级倒立摆的仿真模型如图3所示。“GLlIPState—Space”为直线一级倒立摆的状态空间模型。双击图3中的“Poles Control”模块，打开图4中的设置窗口。

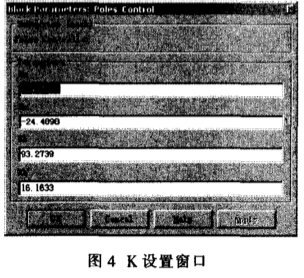
把计算得到的K值输入到上面的窗口。可得图4所示的仿真运行结果。

由图5可见，在存在干扰的情况下，系统在3 s内基本上可以恢复到新的平衡位置。

5、 实时控制

将仿真得到的K参数输入到实际系统的控制模块中，可得图6所示实时控制曲线。在给定倒立摆干扰后，系统响应图7所示。

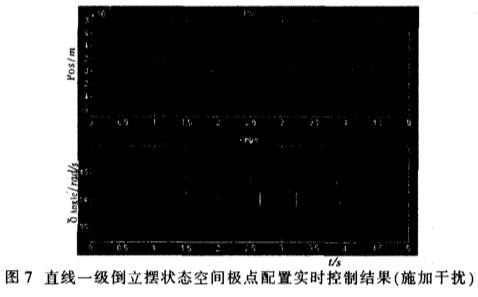
6、 结语

采用极点配置法设计的用于直线型一级倒立摆系统的控制器，可使系统在很小的振动范围内保持平衡，小车振动幅值约为4×10-3m，摆杆振动幅值约0．05 rad，系统稳定时间约3 s。

责任编辑：gt