因果推断和机器学习已有的联系以及应该建立哪些联系

本文认为机器学习和人工智能领域中的待解难题本质上与因果关系有关。

图灵奖得主、贝叶斯网络之父 Judea Pearl 曾自嘲自己是「AI 社区的反叛者」，因为他对人工智能发展方向的观点与主流趋势相反。Pearl 认为，尽管现有的机器学习模型已经取得了巨大的进步，但遗憾的是，所有的模型不过是对数据的精确曲线拟合。从这一点而言，现有的模型只是在上一代的基础上提升了性能，在基本的思想方面没有任何进步。

那么，怎样才能推动 AI 社区解决这一问题呢？Pearl 认为，我们需要一场「因果革命」。研究者应该考虑采用因果推断模型，从因果而非单纯的数据角度进行研究。

近日，马克斯·普朗克智能系统中心主任 Bernhard Schölkopf 发表论文，谈论了因果关系和机器学习之间的联系，并科普了一些相关的重要概念。Judea Pearl 转发相关推文，表示「这是一篇非常全面、令人愉悦且极具启发性的论文」，适合所有人，而不仅仅是机器学习/人工智能从业者阅读。  

机器之心对这篇论文进行了摘要编译，感兴趣的同学可以查看原论文获取更多信息。

论文地址：https://arxiv.org/pdf/1911.10500.pdf

Judea Pearl 开创的图因果推断源自人工智能研究，长期以来与机器学习领域关联甚少。本文讨论因果推断和机器学习已有的联系以及应该建立哪些联系，并介绍其中的核心概念。本文认为机器学习和人工智能领域中的待解难题本质上与因果关系有关，并解释了该领域逐渐理解它们的过程。

引言

近年来，机器学习社区对因果关系的兴趣显著增长。我对因果关系的了解来自于 Judea Pearl 和一些合作者以及同侪，我将其中一些知识写在了与 Dominik Janzing、Jonas Peters 合著作品《Elements of Causal Inference》中。

我曾在多个场合谈论过这个话题，其中一些观点正在融入机器学习主流视角，比如「因果建模能够带来更稳健的模型」。

我很激动能够看到因果和机器学习的交集，这篇文章尝试表达我的思想，并绘制更广阔的图景。我希望本文不仅能够帮助探讨因果思维之于 AI 的重要性，还能够作为入门文章，引导机器学习群体了解图因果模型或结构因果模型的相关概念。

尽管近期机器学习取得了很大成功，但如果我们将机器学习能够完成的事与动物能做的事进行对比，就会发现机器学习对于动物擅长的一些技能表现并不好。这包括将解决问题的能力迁移至新问题，以及任意形式的泛化，这里不是指从一个数据点到另一个数据点的泛化（且数据点来自同一分布），而是从一个问题泛化至下一个问题。

二者虽然都是「泛化」，但后者难度更高。这个缺点并不令人吃惊，因为机器学习是忽视动物严重依赖的信息：对世界的干预、域偏移、时间结构，总体上，我们觉得这些因素很烦并尽量移除。

最后，机器学习还不擅长在想象空间中行动。我认为，关注对干预进行建模和推理的因果关系可以极大地帮助理解和解决这些问题，从而将机器学习领域推向新高度。

从统计模型到因果模型

独立同分布（IID）数据驱动的方法

我们的社区在使用机器学习解决大数据问题上取得了很多成功。这其中呈现出多个趋势：

我们拥有海量数据，这些数据通常来自模拟或大规模人类标注；

我们使用高容量机器学习系统（即具备很多可调整参数的复杂函数类）；

我们使用高性能计算系统；

问题是独立同分布的（IID，这一点经常被忽视，但是在涉及因果关系时，这很关键）。

这些设置通常要么一开始就是 IID（如使用基准数据集的图像识别），要么被人工处理为 IID，如为给定的应用问题精心收集合适的训练数据集，或者使用类似 DeepMind「经验回放」（experience replay）的方法，即强化学习智能体存储观测结果稍后再打乱以便后续训练。

IID 数据具备统计学理论中的强泛相合性（strong universal consistency），这确保学习算法可以最小风险获得收敛。此类算法确实存在，比如最近邻分类器和支持向量机。

从这个角度看，在提供足够数据的前提下，机器达到甚至超过人类性能也无可厚非。但是，当机器面对的问题不遵循 IID 假设时，那么即使这类问题对 IID 假设的破坏在人类看来微不足道，机器也通常很难解决。

当一个能以高准确率被正常识别的物体被放进与该物体出现场景呈负相关的场景训练集时，视觉系统很容易被误导。例如，此类系统可能无法识别站在沙滩上的奶牛。

更夸张的是，「对抗脆弱性」（adversarial vulnerability）现象强调，即使对 IID 假设作出非常微小但有针对性的破坏（这类破坏可以通过向图像添加精心选择的噪声来实现，而人类无法察觉此类更改），也会造成危险的错误，比如混淆交通标志。

近年来，「防御机制」和之后很快出现并重新确立问题的新型攻击展开了攻防战。总体上，大量（试图解决 IID 基准问题的）当前实践和大部分（关于 IID 设置泛化的）理论结果无法解决在不同问题上进行泛化这一待解难题。

为了进一步了解 IID 假设究竟哪里有问题，我们先来考虑一个购物案例。假设爱丽丝在网上查找电脑包，网店的推荐系统建议她搭配购买一台笔记本电脑。这看起来很奇怪，因为她很可能已经买过笔记本电脑了，不然她也不会先看电脑包啊。

在某种程度上，笔记本电脑是「因」，电脑包是「果」。如果有人告诉我某位顾客是否购买过笔记本电脑，那么我对顾客是否购买过电脑包的不确定性会减少，且反之亦然。二者对我的影响是同等程度的（互信息），所以因果之间的方向性丢失了。

然而，这种情况出现在生成统计相关性（statistical dependence）的物理机制中，例如使拥有笔记本电脑的顾客想要购买电脑包。推荐待购买物品构成了对系统的干预，超出了 IID 设置。我们不再处理观测数据分布，而是某些变量或机制已经发生改变了的分布。这就属于因果关系的范畴了。

Reichenbach (1956) 明确指出了因果关系和统计相关性之间的联系。他提出共同原因原理（Common Cause Principle）：如果两个观测对象 X、Y 具备统计相关性，则存在变量 Z 对二者造成因果作用，且通过使它们基于 Z 互相独立来解释二者之间的相关性。

在特殊情况下，变量 Z 可与 X 或 Y 重叠。假设 X 是鹳鸟的数目，Y 是人类出生率（在一些欧洲国家中，二者具备相关性）。如果是鹳鸟带来了人类婴儿，则正确的因果图是 X → Y。如果是婴儿吸引来了鹳鸟，则因果图是 X ← Y。如果某个其他变量引出了这两者（如经济发展），则因果图为 X ← Z → Y。

我们可以从中得出一个重要结论：在没有额外假设的情况下，我们无法利用观测数据区分这三种情况。在这三个案例中，X 和 Y 的观测分布类别（可通过模型得到）是相同的。因此，因果模型所包含的信息超出统计模型。

鉴于仅有两个观测对象的案例已经很难，我们会思考，包含更多观测对象的案例是否完全没有希望解决呢？

令人惊讶的是，事实并非如此：一定意义上这类问题变得更加简单了，因为这类问题中存在因果结构暗含的非平凡条件独立性（nontrivial conditional independence）属性。这类属性可以通过因果图或结构因果模型来描述，它们集成了概率图模型和干预（intervention）概念，最好使用直接的函数式父子（parent-child）关系来描述，而不是使用条件句（conditional）。

尽管现在看来其概念很简单，但它构成了理解因果关系的关键一步，正如 Pearl (2009a, p. 104) 后来所述：

我们研究用函数式父子关系 X_i = f_i(PA_i , U_i) 替代父子关系 P(X_i |PA_i) 的可能性，突然间一切就绪：我们最终得到了一个数学对象，我们可以将物理机制中的熟悉属性归因于它，而不是归因于那些狡猾的认知概率 P(X_i |PA_i)，它也是我们在贝叶斯网络研究中长期研究的对象。

结构因果模型（SCM）

对于更习惯于用估计函数而非概率分布来思考问题的机器学习研究者而言，SCM 比较直观。SCM 提供了一组观测对象 X_1, . . . , X_n（被建模为随机变量），它们与有向无环图（DAG）G 的顶点相关联。我们假设每个观测对象是一个任务的结果：  

该公式使用确定性函数 f_i，该函数依赖于 X_i 在图中的父亲 PA_i 和随机未解释变量 U_i。图中的有向边表示直接因果关系，因为父亲通过有向边与 X_i 相连，并通过公式 (1) 直接影响 X_i 的任务。噪声 U_i 确保整体目标 (1) 表示通用条件分布 p(X_i |PA_i)，噪声集合 U_1, . . . , U_n 是联合独立的。如果它们不是这样，则根据共同原因原理，应存在另一个变量引起它们的相关性，因而该模型不具备充足的因果关系。

如果我们指定 U_1, . . . , U_n 的分布，则对 (1) 的递归应用使得我们能够计算得到的观测联合分布 p(X_1, . . . , X_n)。该分布具备继承自图的结构属性：它满足因果马尔可夫条件，即基于其父亲，每个 X_j 都独立于其非后代。

直观上，我们可以将独立噪声想象为在图中扩展的「信息探针」（类似于在社交网络中蔓延的闲话的独立元素）。其信息互相纠缠，以条件依赖性的足迹呈现，反映出使用独立性检验从观测数据中推断出图结构属性的可能性。

就像刚才那个闲话的类比一样，该足迹不足以确定独特的因果结构。具体来说，如果只有两个观测对象，它肯定无法确定因果结构，因为任意非平凡条件独立性语句都至少需要三个变量。

过去十年，我们一直研究双变量问题。我们意识到通过额外的假设可以解决该问题，因为不仅图拓扑在观测分布中留下足迹，函数 f_i 也是如此。这一点对于机器学习而言非常有趣，在机器学习中大量注意力被倾注在函数类的属性上（如先验或容量度量），稍后我们再讨论这一点。

在讨论之前，我们需要注意 (1) 的其他两个属性。首先，SCM 语言可以直接将干预公式化为修改任务 (1) 子集的运算，如更改 U_i 或将 f_i（X_i）设置为常量。其次，具备噪声联合独立性的图结构说明可将从 (1) 得到的联合分布正准分解为因果条件句，这又叫做因果（或解纠缠，disentangled）分解  

尽管存在很多其他纠缠分解，如  

但公式 (2) 是唯一一个将联合分布分解为结构任务 (1) 对应条件句的分解形式。我们认为它们是解释观测对象之间统计相关性的因果机制。因此，与 (3) 相反，该解纠缠分解将联合分布表示为因果机制的积。

统计学习的概念基础是联合分布 p(X_1, . . . , X_n)（其中通常存在一个 X_i 是 Y 指定的反应变量），我们假设要逼近的函数类是回归 E(Y |X)。因果学习考虑更多类的假设，且寻求利用联合分布具备因果分解 (2) 这一事实。它涉及因果条件句 p(X_i | PA_i)（即 (1) 中的函数 f_i 和 U_i 分布）、这些条件句彼此之间的关联，以及它们容许的干预或更改。稍后我们将进行详细讨论。

因果建模的层级

我接受过物理学训练，喜欢将一组耦合微分方程作为建模物理现象的黄金标准。它帮助我们预测系统的未来行为，推断干预对系统的影响，以及通过适当的平均步骤预测耦合时间演化生成的统计相关性。此外，它还允许我们获得对系统的见解，解释其运作，尤其是获取其因果结构。下面是一组耦合微分方程  

其初始值 x(t_0) = x_0。根据皮卡-林德勒夫定理，如果 f 满足利普希茨条件，则至少在局部范围内，存在唯一解 x(t)。这表明，x 最近的未来值将由其之前的值决定。  

基于此，我们可以确定向量 x(t) 的哪些条目导致 x(t+dt)，即因果结构。这说明，如果我们拥有一个可使用此类常微分方程 (4) 进行建模的物理系统，且该系统的解为 dx/dt（该导数仅出现在公式 (4) 的左侧），则我们可以直接读取其因果结构。

微分方程是对系统相对完整的描述，统计模型则可视为较为粗浅的描述。它通常不会谈及时间，相反，它告诉我们在实验条件不变的情况下某些变量如何执行对其他变量的预测。例如，如果我们使用某种类型的噪声驱动微分方程系统，或者按时间进行平均，则 x 的组件之间可能出现统计相关性，并被机器学习利用。

此类模型不能预测干预的作用，但是其优势在于，它通常基于数据学得，而微分方程通常需要智慧的人类来提出。因果建模位于这两个极端之间，它旨在提供对干预的理解，并预测其影响。因果发现和学习试图在仅使用弱假设的前提下，以数据驱动的方式获得此类模型。

表 1 总结了整体状况，该表基于 Peters 等人（2017）的论文内容进行了改编。

表 1：模型的简单分类。最详细的模型（第一行）是机械/物理模型，通常以微分方程的形式呈现。而另一个极端（最后一行）是纯统计模型，它可从数据中学得，但无法对建模副现象（epiphenomenon）之间关联以外的事情提供见解。因果模型是中间派，既抽象了物理实在（physical realism）又保留了回答特定干预或反事实问题的能力。读者可以查阅 Mooij 等人（2013）的论文，了解物理模型和结构因果模型之间的正式联系。

独立因果机制

现在回到联合分布 p(X_1, . . . , X_n) 的解纠缠分解 (2)。根据因果图，当 U_i 是独立的时，该分解通常是可行的，但是我们现在要考虑 (2) 中因子之间的独立性这一额外概念。我们可以利用视错觉 Beuchet Chair 来非正式地介绍它，如图 1 所示。

图 1：Beuchet Chair 由两个单独物体构成，从破坏了物体和感知过程独立性的特定视角看，它们「组成」了一把椅子。

我们在感知物体时，大脑会假设该物体和其光线所包含信息抵达大脑的机制是相互独立的。我们可以从特定视角观看该物体，来破坏这一假设。如果我们这么做了，则感知会出错：在 Beuchet Chair 的例子中，我们感知到椅子的三维结构，而现实中并没有这样一把椅子。

上述独立性假设是有用的，因为在实践中，它符合绝大多数情况，因此我们的大脑依赖独立于特定视角和光照的物体。类似地，不应出现偶然巧合，比如以 2D 形式组合的 3D 结构，或者与纹理边界重合的阴影边界。在视觉研究中，这叫做通用视角假设（generic viewpoint assumption）。

同样地，如果我们围绕该物体移动，则特定视角随之改变，但我们假设整体生成过程中的其他变量（如光照、物体位置和结构）不受此影响。这是上述独立性所暗含的不变性，允许我们即使在没有立体视觉（运动恢复结构，structure from motion）的情况下也能推断 3D 信息。极端破坏此原则的一个例子是头戴式 VR 设备，它追踪感知者的头部位置，并对设备进行相应的调整。此类设备创建了与现实不对应的视觉场景。   我们再来看另一个例子，假设一个数据集包含海拔高度 A 和年均气温 T。A 和 T 具备相关性，我们认为其原因在于高度对温度有因果作用。假设我们有两个这样的数据集，一个是奥地利，一个是瑞士。则两个联合分布可能截然不同，因为海拔高度的边缘分布 p(A) 不同。

但是，条件句 p(T|A) 可能是类似的，因为它们描述基于高度生成温度的物理机制。然而，当我们仅关注整体联合分布，缺乏因果结构 A → T 的相关信息时，这种相似性就丢失了。因果分解 p(A)p(T|A) 包含的组件 p(T|A) 可泛化至不同国家，而纠缠分解 p(T)p(A|T) 不具备这种稳健性。

当我们考虑系统中的干预时，也会出现相同的情况。对于正确预测干预作用的模型，它需要具备稳健性，能从观测分布泛化至特定干预分布。

我们可以将以上见解表述如下：

独立因果机制（ICM）原理。系统变量的因果生成过程由多个自主模块构成，它们彼此之间不会互相影响。在概率案例中，这意味着每个变量基于其原因（即机制）的条件分布不会影响其他机制；

机制相关性度量（measures of dependence of mechanisms）。注意 p(X_i |PA_i) 和 p(X_j |PA_j ) 这两个机制的相关性不与随机变量 X_i and X_j 的统计相关性重合。在因果图中，很多随机变量具备相关性，即使这些机制是完全独立的。

图 2：如果 f 和 p_x 是独立的，则 p_Y 的峰值可能出现在 f 斜率较小、f^−1 斜率较大的区域。因而 p_Y 包含 f^−1 的信息。  

因果发现

我们回到从观测数据中发现因果关系的问题。如果存在合适的假设，如忠实性，则我们有时可通过执行条件独立性检验从观测数据中恢复底层图的属性。但是，该方法存在一些问题。其中之一是，在实践中，数据集通常是有限的，条件独立性检验是非常困难的问题，尤其是当条件集连续多维时。

因此，尽管原则上不论 SCM 中的函数具备怎样的复杂度，遵循因果马尔可夫条件的条件独立性都成立，但对于有限数据集，条件独立性检验在没有额外假设时是非常困难的。另一个问题是，在仅具备两个变量的案例中，条件独立性的三元概念不成立，因此马尔可夫条件没有有效作用。

对函数类作出假设可以解决上述两个问题。尤其是对机器学习而言，我们都知道在机器学习中，不对函数类进行假设，则有限样本泛化不可能实现。具体而言，尽管一些学习算法是普遍一致的，即在无限样本限制下接近最小预期误差，但对于数据中的任意函数相关性，存在一些收敛很慢的情况。

因此对于给定样本数量，这取决于待学习问题是否达到低预期误差，统计学习理论以函数类复杂度度量提供概率保证。

回到因果关系，我们为 SCM 中函数假设对基于数据学习因果关系的必然性做出了直观解释。考虑一个仅具备两个观测对象的 SCM X → Y，则 (1) 变成：  

且。现在假设 V 是从函数集 F = {f_v(x) ≡ f(x, v) | v ∈ supp(V)} 中选择的随机选择器变量。如果 f(x, v) 以一种不平滑的方式依赖于 v，则从有限数据集中收集 SCM 相关信息是很难的，因为 V 不被观测，它在任意不同的 f_v 之间随机切换。这促进了对复杂度的限制。一种自然的限制是假设一个加性噪声模型  

如果 (7) 中的 f 平滑依赖于 V，V 相对密集，则对复杂度的限制可以通过局部泰勒展开式来促进。它极大降低了函数类的有效规模，如果没有此类假设，则后者会指数级依赖 supp(V) 的基数（cardinality）。

对函数类的限制不仅使从数据中学习函数变得简单，还能够打破双变量案例中因果之间的对称性：给定 X, Y 的分布（由加性噪声模型生成），无法在相反方向拟合加性噪声模型（即 X 和 Y 的角色互换）。这符合特定的泛型假设，U、X 是高斯分布，f 是线性函数的情况属于例外。它推广了 Shimizu 等人（2016）对于线性函数的结论，该观点可泛化至非线性重缩放、循环、干扰因子（confounder）和多变量设置等情况。我们收集了一组因果推断基准问题，目前已有大量方法可以检测出因果方向，其中一些方法基于上述 Kolmogorov 复杂度模型构建，一些则直接学习将双变量分布分类为因果和非因果。

因此，对函数类的假设有助于解决因果推断问题。它们还能够帮助解决基于条件独立性检验的因果发现方法的其他弱点。（条件）独立性检验的近期进展主要依赖核函数类，来表示再生核希尔伯特空间（RKHS）中的概率分布。

因此，我们收集了一些证据，证明机器学习中的想法可以帮助解决之前被认为很难的因果关系问题。但是，相反方向也同样有趣：因果关系能够帮助改善机器学习吗？目前的机器学习（以及现代 AI 的相当多部分）是基于统计建模的，但是随着这些方法变得普遍，其局限性也会更加明显。

不变性、稳健性、半监督学习

大约在 2009 或 2010 年，我们开始对如何利用因果关系改进机器学习感兴趣。具体而言，「神经网络坦克的都市传说」似乎可以说明些什么。在这个故事中，神经网络被训练用于以高准确率分类坦克，但之后发现该网络只是成功地聚焦于包含坦克类型信息的某个特征（如时间段或天气），问题出在数据收集过程中。在不同环境下拍摄的坦克照片上进行测试时，此类系统没有展示出一点稳健性。

我希望包含因果关系的分类器能够对此类变化具备不变性，关于这个主题我之前使用非因果方法研究过 (Chapelle and Schölkopf, 2002)。我们开始思考因果关系和协变量偏移之间的连接。我们知道因果机制应该具备不变性，类似地，任何基于学习因果机制获得的分类器也应该具备不变性。但是，很多机器学习分类器不使用因果特征作为输入，我们注意到它们的确更经常解决非因果问题，即使用结果特征来预测原因。

从 2010 年 4 月在雷伯格举办的院系 retreat 到 2011 年 7 月的 Dagstuhl 研讨会，我与 Dominik、Jonas、Joris Mooij、Kun Zhang、Bob Williamson 等进行了大量讨论，我们关于不变性的想法在此期间逐渐成熟。

当我收到 NIPS 会议 Posner 演讲邀请后，将这些想法构建成结论的压力明显更大了。那时，我需要建设新的马普所，很难匀出时间处理这件事并作出进展。因此，我和 Dominik 决定在黑森林度假屋待一周全力处理这件事。

在 2011 年 11 月的那一周中，我们完成了草稿 invariant.tex，之后不久我们将其投递到 arXiv 网站。这篇论文认为因果方向对于特定机器学习问题非常重要，对协变量偏移保持稳健性（不变性）是可以期待的，对于从因预测果的学习问题，迁移也变得更加简单，这为半监督学习打了头阵。

论文地址：https://arxiv.org/abs/1112.2738

半监督学习（SSL）

假设底层因果图是 X → Y，同时我们尝试学习映射 X → Y。则该案例的因果分解 (2) 为：  

ICM 原理认为联合分布因果分解中的模块无法彼此影响。这意味着，p(X) 不应包含关于 p(Y |X) 的任何信息，即半监督学习是徒劳的，除非它使用来自无标注数据的额外 p(X) 信息来改善对 p(Y |X = x) 的估计。那么反方向呢？半监督学习在相反的情况下是可能的吗？答案是「Yes」，参见第 5 章使用独立因果机制的因果推断研究。

该研究与 Povilas Daniušis 等人合作完成（2010），它提出对输入和给定输入的输出条件句之间相关性的度量方法，并展示了如果该相关性在因果方向上为 0 时，则它在相反方向上为正。因此，因果独立性和因果方向中的机制表明，在反方向中（即非因果学习），输入变量的分布应包含给定输入的输出条件句的信息，即机器学习通常关注的量。我之前研究过半监督学习，现在可以明确的是，当尝试使用无标注输入改进对输出的估计时，给定输入的输出条件句的信息恰是 SSL 所需要的。因此，我们预测 SSL 无法处理因果学习问题，但适合处理非因果问题。

之后的研究也证明了这一点（详情参见原论文）。

对抗脆弱性

你可以假设因果方向应该对分类器能否抵抗对抗攻击产生影响。最近，这类攻击变得流行，它们包含对输入进行的微小更改，人类观察者无法察觉此类更改，但它们确实改变了分类器的输出。

这在多个维度上与因果关系相关。首先，这些攻击明确构成了对预测式机器学习的底层 IID 假设的破坏。如果我们想做的是在 IID 设置下执行预测，则统计学习完全足够。而在对抗环境下，修改后的测试样本和训练样本不来自同一个分布：它们构成了干预，干预经优化后可用来揭示（非因果）p(y|x) 的非稳健性。

对抗现象还说明目前分类器所具备的稳健性与人类不同。如果我们知道两种稳健性度量，我们会尝试最大化其中一个、最小化另外一个。目前的方法可被视为对此的粗略逼近，将人类的稳健性有效建模为简单的数学集合，如半径 > 0 的球 l_p：它们通常试图找出给分类器输出带来最大改变的样本，不过需遵循一项限制，即这些样本必须在 l_p 球内（以像素度量形式）。这也导致对抗训练的步骤类似于在「虚拟」样本上训练分类器使其具备不变性的旧方法。

现在，考虑将模型分解为多个组件（参见 (3)）。如果这些组件对应因果机制，则我们预计模型具备一定程度的稳健性，因为因果机制是自然属性。具体而言，如果我们在因果方向上学习分类器，则该分类器具备一定的稳健性。你可能因此假设，对于因果学习问题（从因预测果），我们不可能或至少更难找到对抗样本。近期研究支持这一观点：通过建模因果生成方向来解决非因果分类问题是一种有效的对抗攻击防御方法，在视觉领域中该方法叫做合成分析（analysis by synthesis）。

更广泛来讲，对于具备两个以上顶点的图，我们可以推断出其结构由多个自主模块构成，如因果分解 (2) 所提供的组件，这类结构应该对置换或修改单个组件具备一定的稳健性。稍后我们再来讲这个话题。

稳健性还应该在研究策略行为时发挥作用，策略行为即考虑其他智能体（包括 AI 智能体）的动作后所做出的决策或动作。考虑一个试图基于一组特征预测成功偿还信用卡概率的系统。这组特征包括个人当前债务及其地址。为了得到更高的信用积分，人们会（通过偿还行为）更改其当前债务金额，或者将个人地址更换到更富裕的地区。前者对偿还债务的概率有正面的因果作用，而后者则相反。因此，我们可以仅使用因果特征作为输入，构建一个对此类策略行为具备更强稳健性的得分系统。

多任务学习

假设我们想构建一个在多个环境中解决多个任务的系统。此类模型可以利用学习视角作为压缩。基于训练集 (x_1, y_1), . . . ,(x_n, y_n) 学习函数 f（从 x 到 y 的映射）可被视为 y 基于 x 的条件压缩。其思路是，我们可以找出最紧凑的系统来基于 x_1, . . . , x_n 恢复 y_1, . . . , y_n。

假设爱丽丝想与鲍勃交流标签，二人均知道输入。首先，他们商定将要使用的函数 F 的有限集。然后爱丽丝从函数集中选出最优函数并告诉鲍勃（选取函数的数量取决于函数集大小，也可能取决于二人商定的先验概率）。此外，爱丽丝可能还要告诉鲍勃函数无法正确分类的输入 x_i 的索引 i，即 f(x_i) ≠ y_i。

在选择大量函数类（编码函数索引需要很多成本）和允许大量训练误差（需要分开编码）之间存在权衡。该权衡完美对应统计学习理论中的标准 VC 边界（standard VC bound）。

你可以将其泛化至多任务环境：假设我们有多个数据集，它们从类似但不相同的 SCM 中采样得来。如果这些 SCM 共享大部分组件，则我们可以通过编码 SCM 中的函数来压缩从多个 SCM 中采样得到的多个数据集。正确的结构（在双变量案例中，这应该等于正确的因果方向）应该是最紧凑的一个，因为它包含多个数据集共享的多个函数，因此只需要执行一次编码即可。

强化学习

将统计学习向因果学习推动的计划与强化学习也有关系。强化学习过去（现在通常也）被认为是很难处理现实世界高维数据的学习方法，原因之一是作为反馈的强化信号相比监督学习中的标签信息要稀疏很多。DeepQ 智能体取得了当时社区认为不可能实现的结果，但与动物智能相比它仍然存在一些显著缺陷。其中两个主要问题可以表述为：

问题 1：为什么强化学习在原始高维 ATARI 游戏中要比在降采样版本中更难？

对于人类而言，降低游戏屏幕分辨率会使问题变难，这正是 DeepQ 系统的运行原理。动物可以根据「共同命运」或对干预的共同反应，对像素进行分组，从而识别物体（在计算机游戏中这叫做「sprite」）。因此该问题与「物体由什么构成」这个问题相关，后者不仅关乎感知还涉及我们与世界的交互方式。我们可以捡起某个物体，但无法捡起半个物体。因此物体也对应可被单独干预或操控的模块化结构。物体由变换下的行为来定义，这个深刻观点不仅适用于心理学，也适用于数学。

问题 2：为什么在打乱重放（replay）数据后，强化学习会变得简单？

因为智能体在世界中游荡时，它对其看到的数据产生影响，因而统计数据随着时间发生改变。这破坏了 IID 假设，如前所述，DeepQ 智能体存储之前数据并在其上重新训练（作者将该过程比作做梦），从而利用标准 IID 函数学习技术。但是，时间顺序包含动物智能所使用的信息。信息不仅包含在时间顺序中，还包含在统计数据的缓慢改变能够高效创建多域设置这一事实中。

多域数据被证明有助于识别因果（也是稳健）特征，更广泛来讲，它可以寻找不变性，从而搜寻因果结构。这有助于强化学习智能体找到模型中的稳健组件，这些组件有望泛化至状态空间的其他部分。一种方式是使用 SCM 部署基于模型的强化学习，该方法可以帮助解决强化学习中的干扰问题，在这类问题中时间变化和时间不变的未观测干扰因子会影响动作和奖励。   在此类方法中，非平稳性是特征而非 bug，智能体积极寻找不同于已知区域的区域，以挑战现有模型，并了解哪些组件具备稳健性。这种搜索可被视为一种内在动机，该概念与动物行为学中的潜在学习（latent learning）有关，它在强化学习中得到了重视。

最后，因果学习中还有一个巨大的开放区域是与动态过程的连接。我们可能天真地以为因果关系通常与时间有关，但大部分现有因果模型并非如此。例如海拔高度与温度那个例子，底层的时间物理过程确保更高的地方温度更低。在涉及粒子运动的微观方程层次上，存在清晰的因果结构（如上所述，微分方程确切指明变量的哪些之前值对当前值产生影响）。   但是，在提及高度和温度之间的相关性或因果关系时，我们无需担忧时间结构的细节，我们使用的数据集没有出现时间信息，我们可以推断对温度或高度进行干预后，数据集会变成什么样。我们需要思考如何在这些不同的描述层次之间架起桥梁。

在推导出能够描述耦合系统干预行为的 SCM 方面已经取得了一些进展，耦合系统处于均衡状态，且可以用「绝热」方式干扰，并泛化至振动系统。为什么简单的 SCM 通常是可推导的？这不存在根本性原因。SCM 是对微分方程底层系统的高级抽象，此类方程只在合适的高级变量被定义时才能够被推导，这可能是例外而非规则。

相比机器学习主流，强化学习与因果关系研究更接近，因为它有时高效直接地估计执行某个行为的概率（在策略学习）。但是，一旦涉及离策略学习，特别是在批量（或观测）设置下，因果关系的问题就变得很微妙。

因果表示学习

传统的因果发现和推理假设单元是由因果图连接的随机变量。但是，现实世界观测结果通常无法在一开始就结构化为这类单元，如图像中的对象。因果表示学习这一新兴领域致力于从数据中学习这些变量，就像超出符号 AI 的机器学习，不需要为算法操控的符号提供先验。定义与因果模型相关的对象或变量等同于对更详细的世界模型进行粗糙模仿。   在合适的条件下，对微观模型的粗糙模仿可以产生结构模型，这些微观模型包括微观结构方程模型、常微分方程和时间聚合时序（temporally aggregated time serie）。尽管经济学、医疗或心理学中的每一个因果模型使用的变量是对较初级概念的抽象，但是表述粗糙变量容许因果模型（具备定义规范的干预）的通用条件是很有难度的。

识别容许因果模型的合适单元这一任务对于人类和机器智能都有难度，但是它与现代机器学习学习有意义的数据表示这一通用目标是一致的，「有意义」表示稳健、可迁移、可解释或公平。为了结合结构因果建模 (1) 和表示学习，我们应将 SCM 嵌入到更大的机器学习模型中，该模型的输入和输出可能是高维和非结构化的，但是其内在工作机制至少部分受 SCM 控制。实现这一点的一种方式是，将未解释变量实现为生成模型中的（潜在）噪声变量。   此外，还需注意 SCM 和现代生成模型之间存在自然连接：它们都使用重参数化技巧，包括使期望随机性作为模型的（外生）输入（在 SCM 中，这些是未解释变量）而非内在组件。

学习可迁移机制

复杂世界中的人工或自然智能体面临的资源有限。这涉及到训练数据，即每个任务/领域的数据有限，因此需要寻求池化/数据重用方法，这与人类执行大规模标注工作的当前行业实践形成鲜明对比。它还涉及计算资源的问题：动物的大脑规模存在限制，进化神经科学中有很多大脑区域被重新规划的示例。   类似的规模和能量限制也出现在机器中，因为机器学习方法嵌入的（小型）物理设备可能是电池供电。因此，未来稳健地解决大量现实问题的 AI 模型有可能需要重用组件，这要求组件对多个任务和环境具备稳健性。

实现该目标的一种优雅方式是，利用能够反映世界对应模块的模块化结构。换言之，如果世界确实是模块化的，那么一定程度上世界的不同组件在大量环境、任务和设置中发挥作用，模型需要谨慎利用对应模块。例如，如果自然光线的变化（如太阳、云的位置等）表明视觉环境的光照条件多达数个数量级，则人类神经系统中的视觉处理算法应利用能够因子化这些变化的方法，而不是针对每一种光照条件构建不同的人脸识别器。

如果我们的大脑能够通过增益控制机制弥补光线变化，那么该机制无需与带来光照变化的物理机制有任何关系。但是，它会在模块化结构中发挥作用，这对应于物理机制在世界的模块化结构中的作用。这会使向我们无法直接识别的世界展示特定形式的结构同构（structural isomorphism）的模型出现偏差，这很有趣，因为最终我们的大脑什么都没做，只是将神经元信号转换为其他神经元信号。

学习此类模型的合理归纳偏置是寻找独立因果机制，有竞争力的训练可以发挥作用：对于模式识别任务，Parascandolo 等人（2018）展示了学习包含独立机制的因果模型有助于在迥异领域中实现模块迁移。在这篇研究中，手写字符被一组未知机制（包括平移、噪声和对照倒置）扭曲。神经网络试图通过一组模块去除这些变换，这组模块中的每一个都专注于一个机制。

对于任意输入，每个模块尝试生成正确的输出，然后判别器来分辨哪个模块效果最好。获胜的模块通过梯度下降进行训练，进一步提升其对该输入的性能。最终系统学得平移、倒置或去噪等机制，这些机制可迁移至来自其他分布的数据，如梵语字符。近期，这已发展到新的阶段：将一组动态模块嵌入到循环神经网络中，注意力机制对此进行协调。这使得学习模块的动态过程大部分时间独立运转，但偶尔也会彼此交互。

学习解纠缠表示（disentangled representation）

上文我们探讨了 ICM 原理，它既表明 (1) 中 SCM 噪声项的独立性，又进而说明解纠缠表示具备可行性：  

以及条件句 p(S_i | PA_i) 可被独立操控，且在大量相关问题上具备强大的不变性。假设我们希望利用来自数据的独立机制 (11) 重建此类解纠缠表示，但是没有因果变量 S_i 作为先验，只有（可能是高维度的）X = (X_1, . . . , X_d)（下文中，我们将 X 想象为具备像素 X_1, . . . , X_d 的图像），基于此我们应构建因果变量 S_1, . . . , S_n (n << d) 以及机制（参见 (1)），  

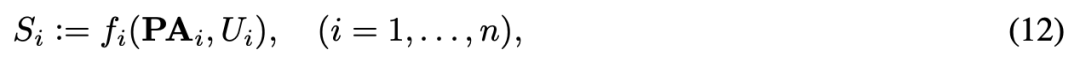
建模 S_i 中的因果关系。为此，我们首先使用编码器 q : R^d → R^n 将 X 输入潜在「瓶颈」表示，该表示包含未解释噪声变量 U = (U_1, . . . , U_n)。然后是结构化任务 f_1, . . . , f_n 确定的映射 f(U)。最后，我们使用解码器 p : R^n → R^d。如果 n 足够大，则该系统可利用重建误差训练，以在观测图像上满足 p ◦ f ◦ q ≈ id。为了使其具备因果关系，我们使用 ICM 原理，即我们应使 U_i 具备统计独立性，使机制 f_i 独立。这可以通过确保它们对多个问题具备不变性或可被独立干预来实现：如果我们操控其中一些，它们应该仍能生成有效图像，这可以通过生成对抗网络的判别器来训练。

我们完美地操控了完整机制 f_i，现在我们来讨论干预潜在噪声变量的特例。一种干预方式是用基于其他输入图像计算出的对应值替换噪声变量，该步骤被 Besserve 等人 (2018b) 称为「杂合」（hybridization）。在极端情况下，我们可以杂合每个组件都计算自另一个训练样本的潜在向量。对于 IID 训练设置，这些潜在向量具备统计独立性组件。

在此类架构中，编码器是识别或重建世界中因果驱动因素的非因果映射。这样，机制可被公式化，也可在不同任务中迁移。解码器在（驱动因果模型噪声的）低维潜在表示和高维世界之间建立连接，这部分构成了因果生成图像模型。ICM 假设表明，如果潜在表示重建真正的因果变量（以及驱动它们的噪声），则对这些噪声（以及被驱动的机制）的干预是允许的，且能够有效生成图像数据。

学习干预式世界模型（interventional world model）和推理

现代表示学习擅长为保留相关统计属性的数据学习表示。但是，这样做没有考虑到变量的因果属性，也就是说它不关心它所分析或重建变量的干预属性。我希望未来，因果关系可以在推动表示学习更进一步的道路上发挥重要作用，使其超出统计相关性结构的表示，向支持干预、规划和推理的模型前进，实现 Konrad Lorenz「像在想象空间中行动那样思考」的概念。   这最终需要回顾个人行为和设想其他场景的能力，可能需要自由意志。自我意识的生物功能可能与个人的 Lorenzian 想象空间中表示自身的变量有关，自由意志可能是交流该变量所执行动作的方式，这对社会和文化学习都很重要，这个话题尚未进入机器学习研究，尽管它是人类智能的核心。