

第二讲 逻辑代数基础
电子常识
描述
第二讲 逻辑代数基础
2.1 概述
2.2逻辑函数及其表示法
2 . 2 . 1 基本逻辑函数及运算
一、与逻辑
二、或逻辑
三、逻辑非
2.2.2 几种导出的逻辑运算
一、与非运算、或非运算、与或非运算
二、异或运算和同或运算
2.2.3 逻辑函数及其表示法
一、逻辑函数的建立
二、逻辑函数的表示方法
1.真值表
2.逻辑函数式
3.逻辑图
2.1 概述
布尔:英国数学家,1941年提出变量“0”和“1”代表不同状态。
本章主要介绍逻辑代数的基本运算、基本定律和基本运算规则,然后介绍逻辑函数的表示方法及逻辑函数的代数化简法和卡诺图化简法。逻辑代数有其自身独立的规律和运算法则,而不同于普通代数。
2.2逻辑函数及其表示法
2 . 2 . 1 基本逻辑函数及运算
1、与运算 ——— 所有条例都具备事件才发生

开关:“1” 闭合,“0” 断开
灯:“1” 亮,“0” 灭

真值表:把输入所有可能的组合与输出取值对应列成表。
逻辑表达式: L=K1*K2 (逻辑乘)
逻辑符号: 原有符号:
原有符号:
讨论与逻辑运算的逻辑口诀
逻辑功能口决: 有“0”出“0”,全“1”出“1”。
2、或运算 ——— 至少有一个条件具备,事件就会发生。


逻辑表达式:L=K1+K2 (逻辑加)
逻辑符号: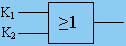
讨论或逻辑运算的逻辑口诀
逻辑功能口决:有“1”出“1”全“0”出“0”
3、非运算: — 结果与条件相反


逻辑表达式: 
逻辑符号: 讨论非逻辑运算的逻辑口诀
讨论非逻辑运算的逻辑口诀
2.2.2 几种导出的逻辑运算
一、与非运算、或非运算、与或非运算

二、异或运算和同或运算

逻辑表达式: 相同为“1”,不同为“0”
相同为“1”,不同为“0”
2.2.3 逻辑函数及其表示法
一、逻辑函数的建立
举例子说明建立(抽象)逻辑函数的方法,加深对逻辑函数概念的理解。
例2.2.1 两个单刀双掷开关 A和B分别安装在楼上和楼下。上楼之前,在楼下开灯,上楼后关灯;反之下楼之前,在楼上开灯,下楼后关灯。试建立其逻辑式。
表2.2.6 [例2.2.1]真值表

例2.2.2 比较A、B两个数的大小
二、逻辑函数的表示方法
1.真值表
逻辑函数的真值表具有唯一性。逻辑函数有n个变量时,共有 个不同的变量取值组合。在列真值表时,变量取值的组合一般按n位二进制数递增的方式列出。用真值表表示逻辑函数的优点是直观、明了,可直接看出逻辑函数值和变量取值之间的关系。
分析逻辑式与逻辑图之间的相互转换以及如何由逻辑式或逻辑图列真值表。
2.逻辑函数式
写标准与-或逻辑式的方法是:
(l)把任意一组变量取值中的1代以原变量,0代以反变量,由此得到一组变量的与组合,如 A、B、C三个变量的取值为 110时,则代换后得到的变量与组合为 A B 。
(2)把逻辑函数值为1所对应的各变量的与组合相加,便得到标准的与-或逻辑式。
3.逻辑图
逻辑图是用基本逻辑门和复合逻辑门的逻辑符号组成的对应于某一逻辑功能的电路图。
例2.2.3 已知真值表,试写出逻辑式并画出逻辑图。
- 相关推荐
- 热点推荐
- 逻辑
-
Protues教程第二讲:动态数码管2023-06-14 4763
-
matlab的经典课件-第二讲2016-09-01 543
-
第二章 逻辑门电路2016-05-20 770
-
高压示波器通俗讲座_第二讲_电源电路2016-05-05 455
-
逻辑代数运算规则2010-09-19 7748
-
逻辑代数和函数化简2010-05-26 778
-
《线性代数实践及MATLAB入门》第二版《线性代数实践》课件2009-10-24 1109
-
逻辑代数基础2009-09-24 3490
-
逻辑代数与逻辑函数2009-09-01 1175
-
逻辑代数基础及基本逻辑门电路2009-07-02 1291
-
第三讲 逻辑代数的基本定律和规则2009-03-30 5868
全部0条评论

快来发表一下你的评论吧 !

