考量运算放大器在Type-2补偿器中的动态响应

考量运算放大器在Type-2补偿器中的动态响应（第二篇）

03

FACT应用于Type-2补偿器

为高效地将FACT运用到Type-2补偿器，我们先考虑储能元件C1和C2。考虑到它们的独立状态可变—如它们不是串联或并联--这是个二阶系统。考虑非零准静态增益，该系统可表示为：  

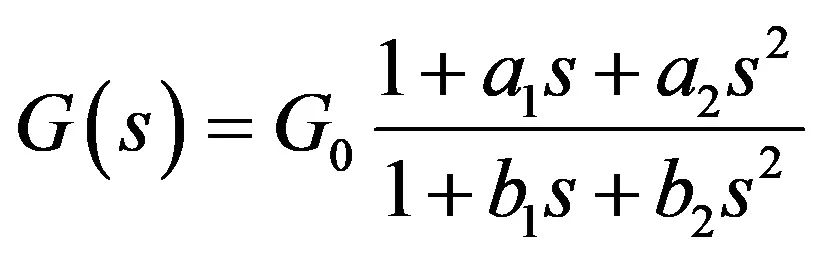
（11）

对于二阶系统，我们可证明分母遵循下列公式：  

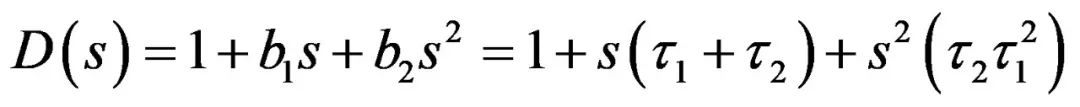
（12）

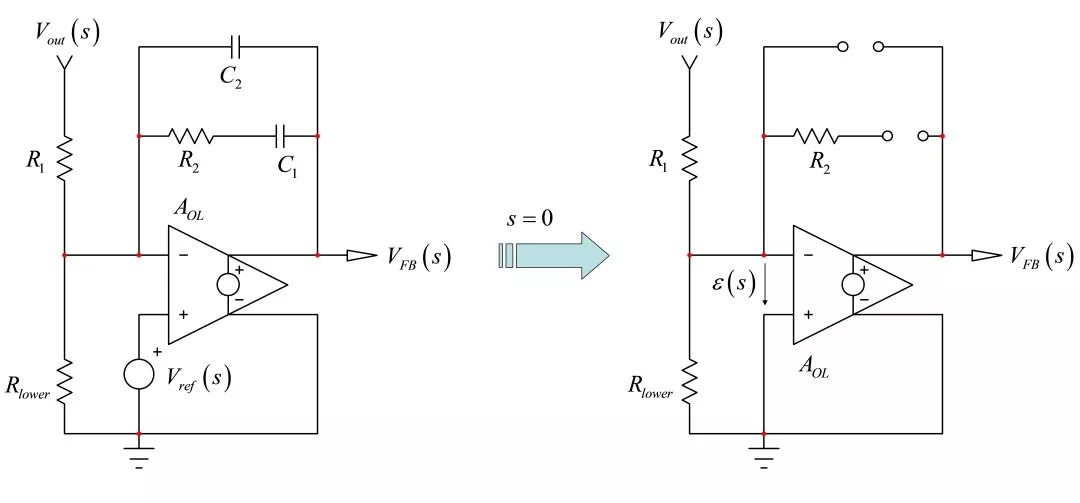
系数s仅是确定零点激励的时间常数之和。S²系数稍复杂，因其引入新符号。此符号意味着您“想象”的C2两端的阻抗，而C1由短路取代。乍一看有点难以理解，但我们稍解释就会明白。   按求解图2电路的途径，我们可研究s=0的系统(图7)。在分析的过程中，Vref是个完美的源及其动态响应为0（忽略我们应用的调制，其电压是固定的）。因此，它自然不存在于小信号电路，在交流分析中为短路的形式。  

图7：在直流条件下，断开所有的电容：运放运行于开环配置。

运放提供的电压相当于开环增益AOL的e倍。反相引脚的电压与低边阻抗Rlower有关，这时e是个非零的值：  

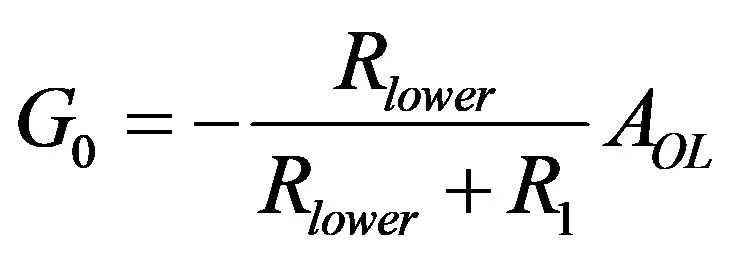
（13）

此电路有两个电容，因此有两个单独的时间常数。为确定与C2有关的第一个时间常数，我们将激励信号设为0，确定C2的阻抗，C2连接端子，而C1从电路中移除。   为确定由C2端提供的阻抗，我们可连接测试生成器IT，和确定其两端的电压VT。然后VT/IT会提供我们想要的阻抗。可写的第一个简单的等式与e有关。运放的输入引脚之间的电压是：  

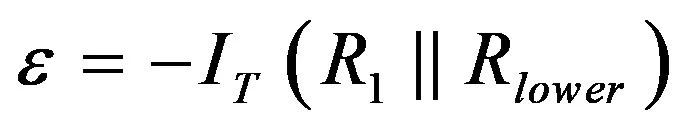
（14）

运放的输出为：  

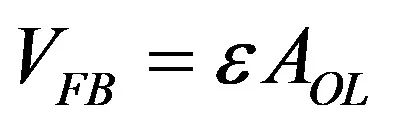
（15）

将(14)代入(15)得出：  

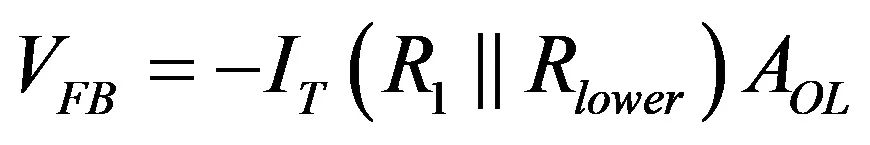
（16）

VT是电流源的电压：  

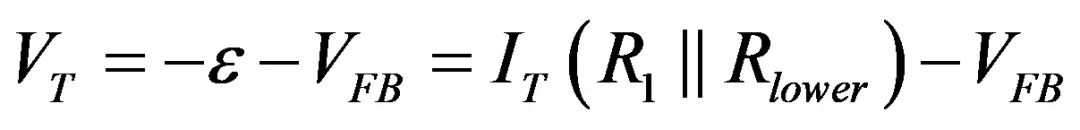
（17）

若从（17）提取VFB，结合（16）的结果，我们有：  

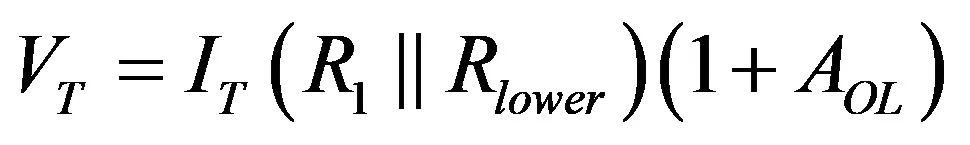
（18）

阻抗是：  

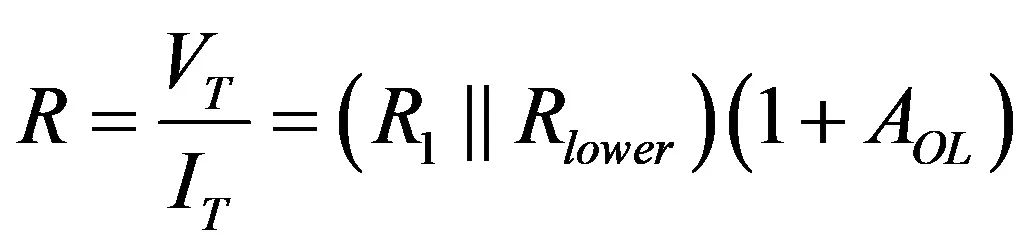
（19）

因此第一个时间常数t2表示为：  

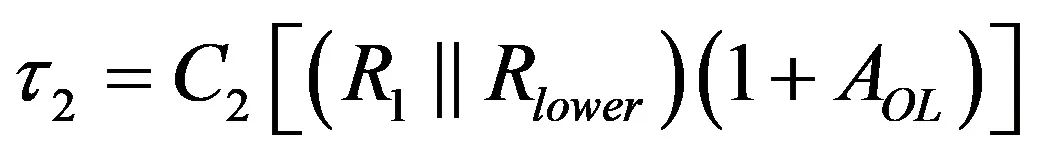
（20）

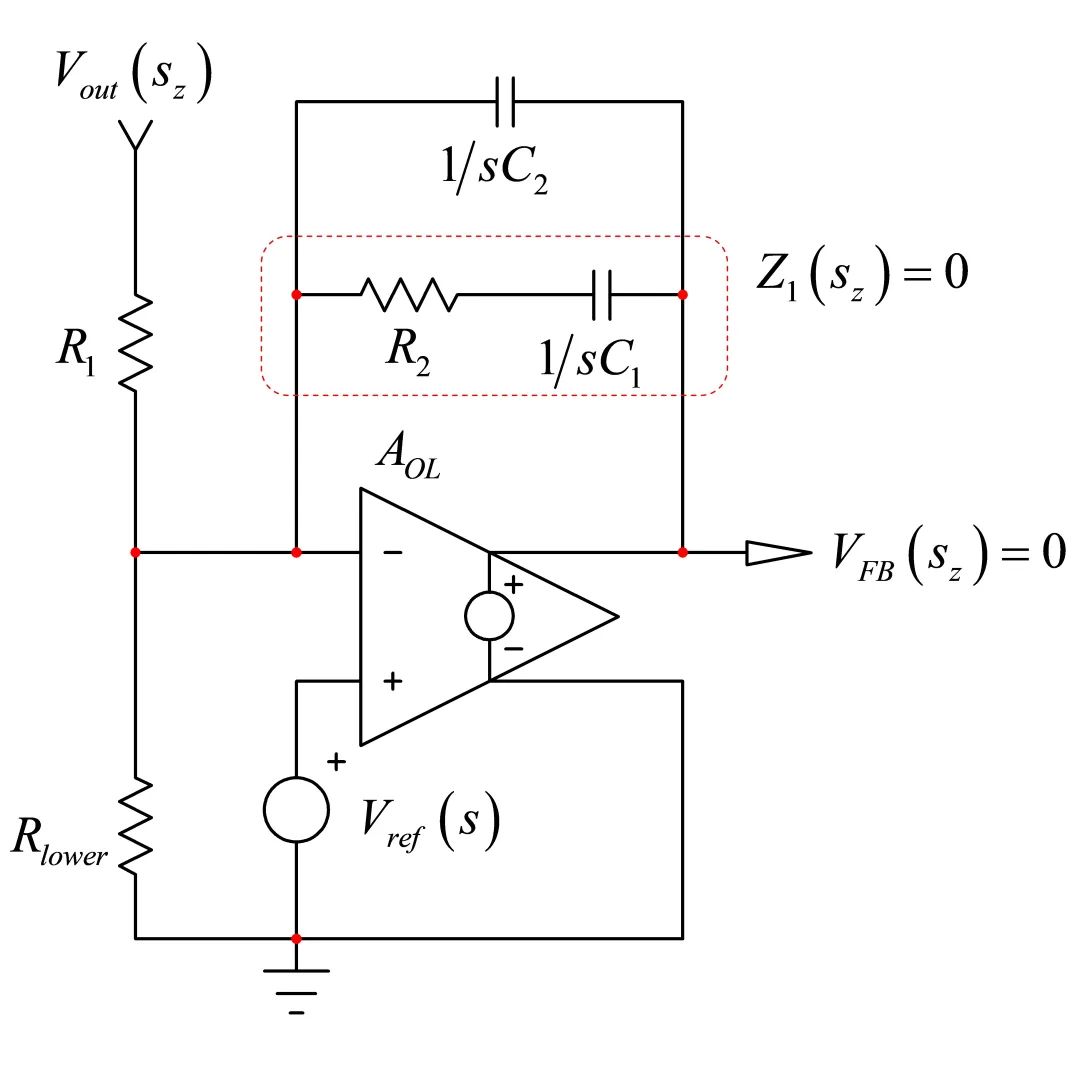
第二个时间常数与C1有关(图8)。我们未安装电流发生器，因为结果很明显：C1两端的电阻就是已确定的C2与R2串联后的电阻：  

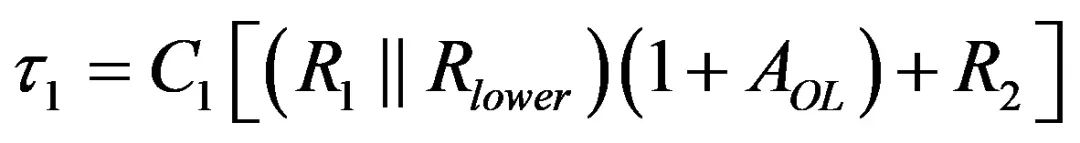
（21）

图8：立即确定第二个时间常数，因为它是C2与R2串联的驱动电阻。

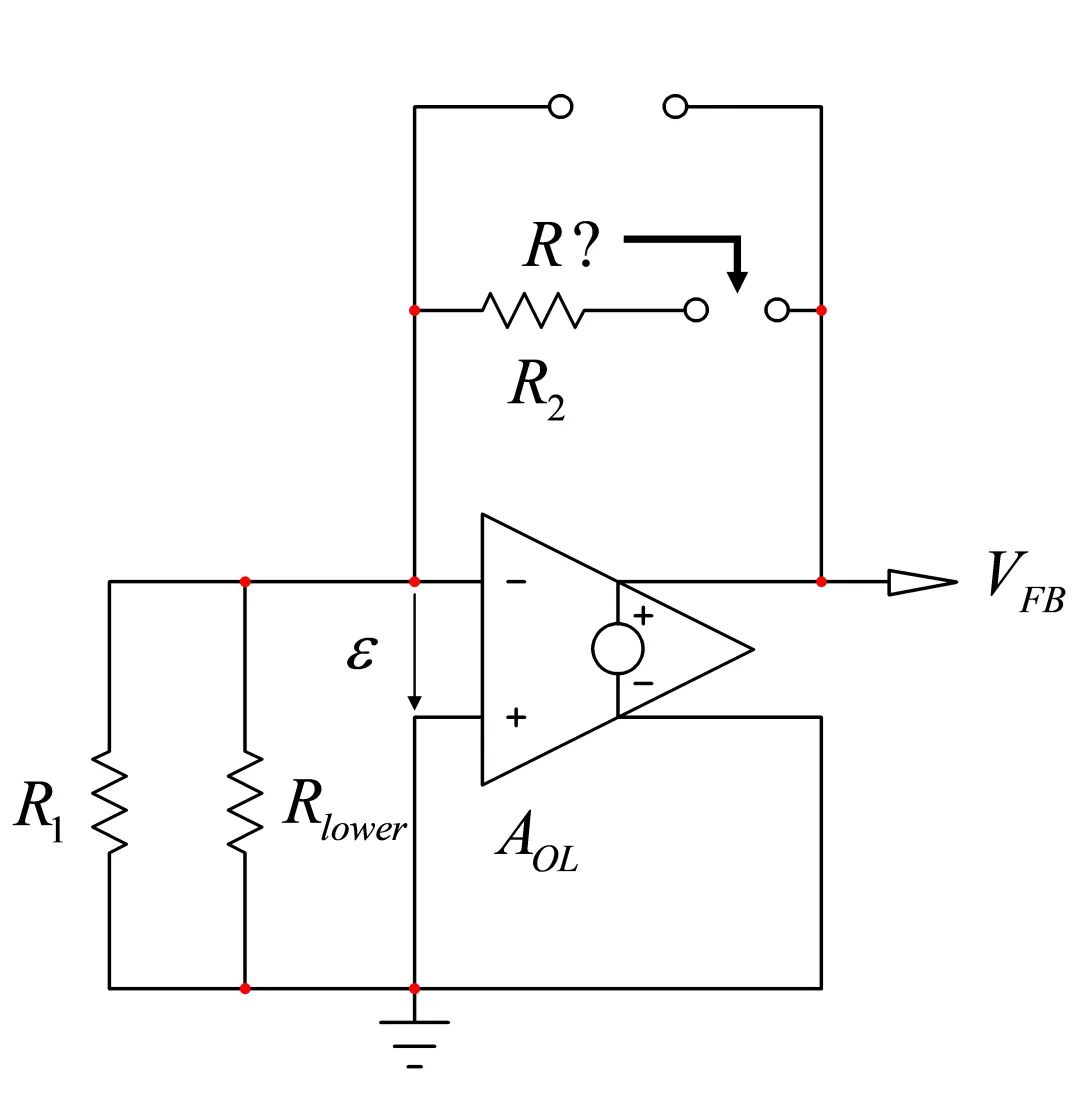
我们有两个时间常数，可进行第二阶项。我们需要评估，其中C2由短路代替，我们看C1端的电阻。既然我们在涉及R2的回路中有弗兰克短路，那么电阻R就是R2：  

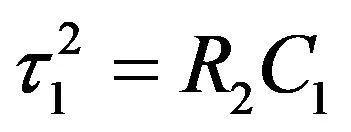
（22）

因此，若我们根据（12）组合时间常数，得出分母D(s) ：  

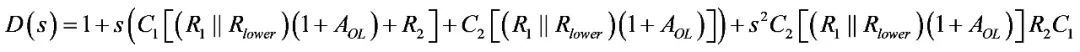
（23）

这二阶形式可重新排列，假设质量因子Q远小于1。此时两个极点完全分离：一个控制低频，而第二个位于频谱的上部。由（12）我们可证明，两个极点定义为：  

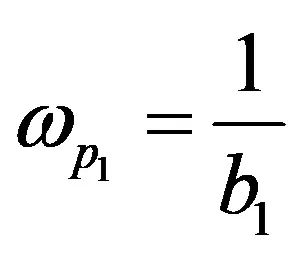
（24）

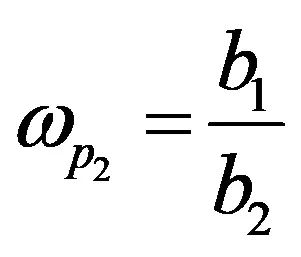
（25）

若我们将这些定义应用到（23），简化和重新排列，得到：  

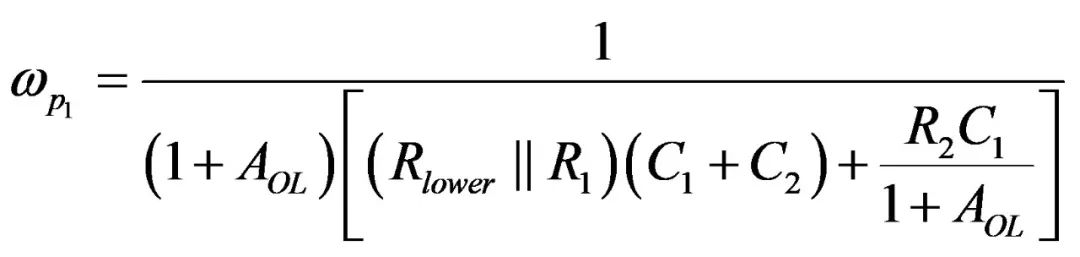
（26）

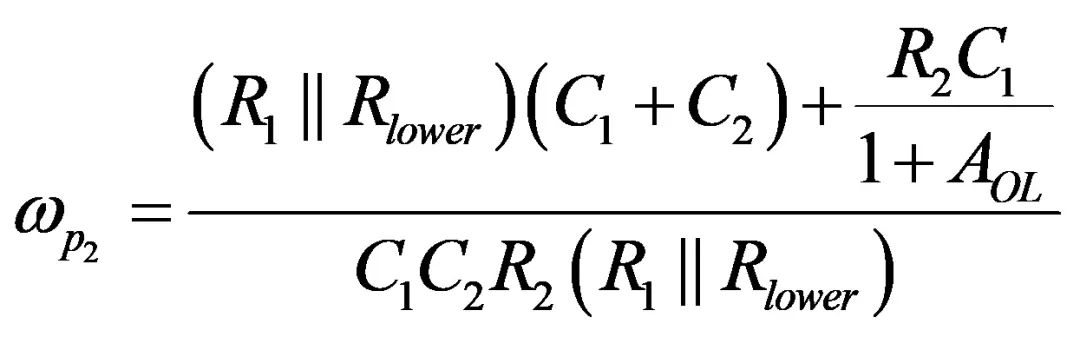
（27）

若我们想象使C1或C2或C1和C2短路，这三个配置有响应吗？若C1短路，我们有一个含R2和其他电阻的简单的逆变器：有个与C1有关的零点。若C2短路，则运放为0：C2没有零点。若两个电容器都短路，当然，没有响应。若C1和R2短路，那么响应消失(图9)：  

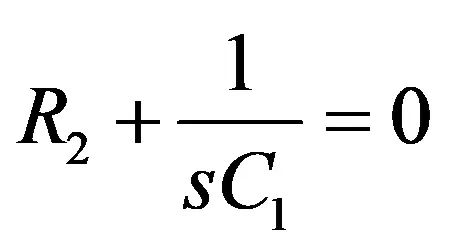
（28）

然后  

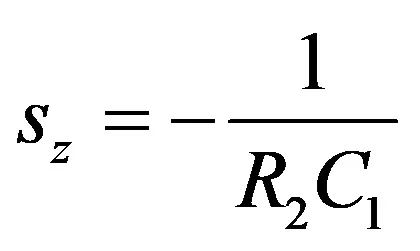
（29）

图9：若R2与C1的串连转换为短路，那是没信号的响应：这就解释了零点是如何产生的。

其中给出了零点位于：  

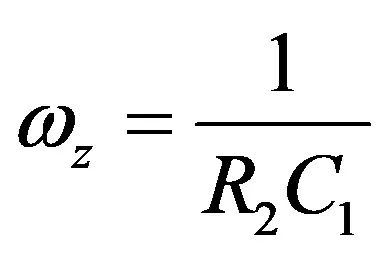
（30）

现在有最终的传递函数  

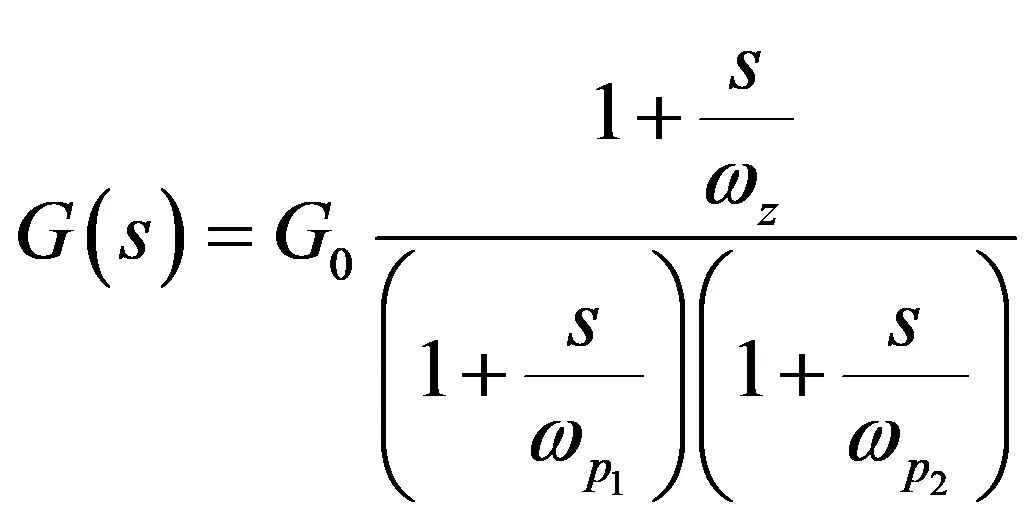
（31）

及  

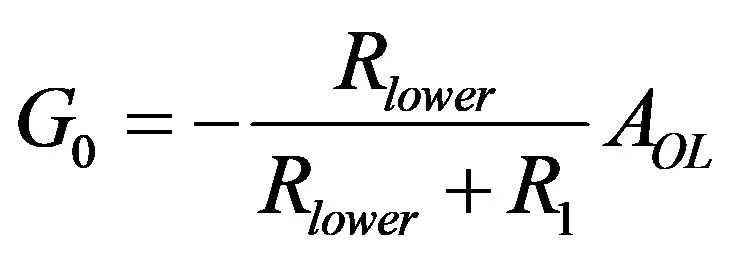
（32）

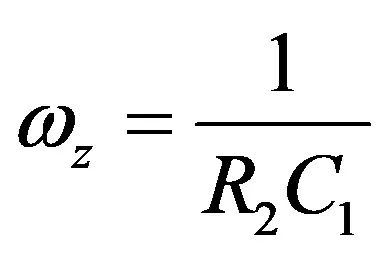
（33）

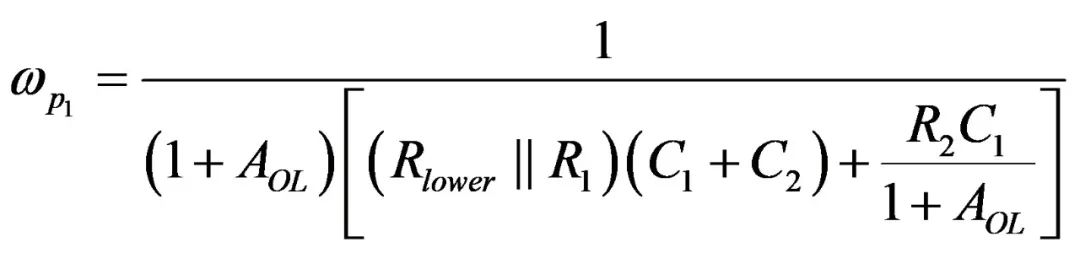
（34）

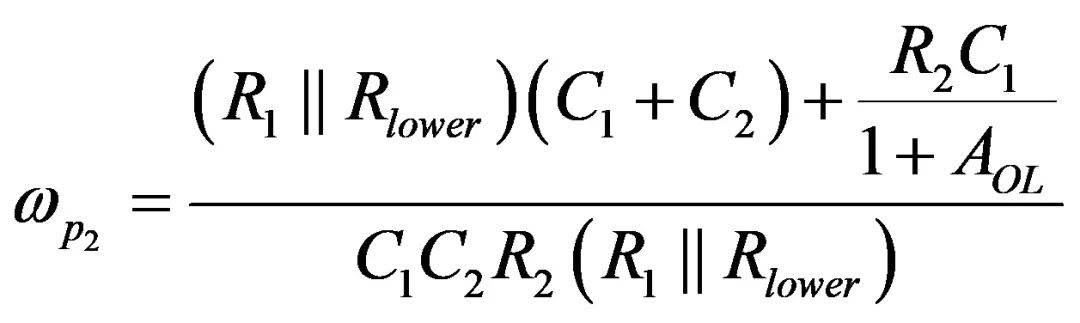
（35）

04

比较电路之间的响应

现在比较由type-2电路(其中我们考虑开环增益)带来的动态响应是有意义的， type 2完美的传递函数为：  

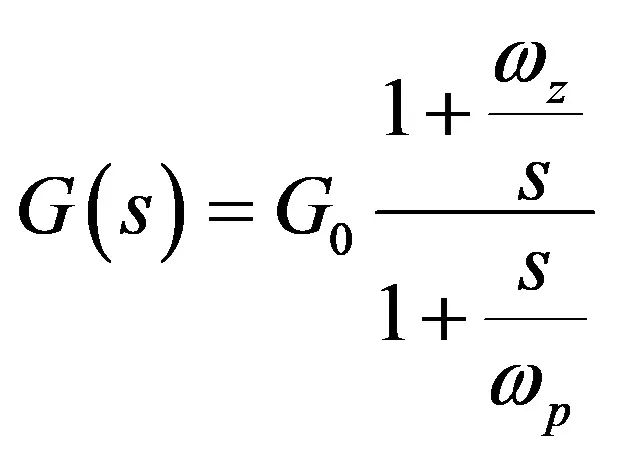
（36）

其中  

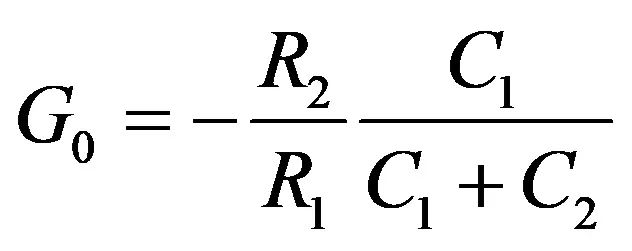
（37）

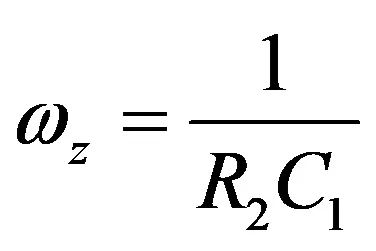
（38）

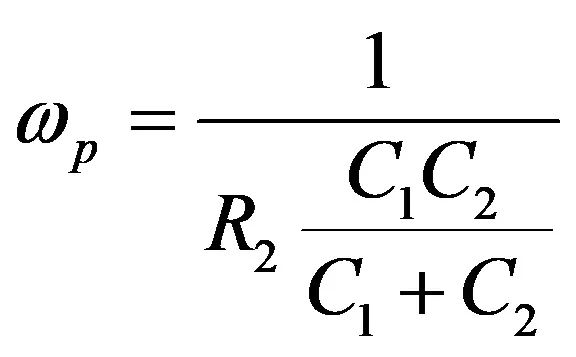
（39）

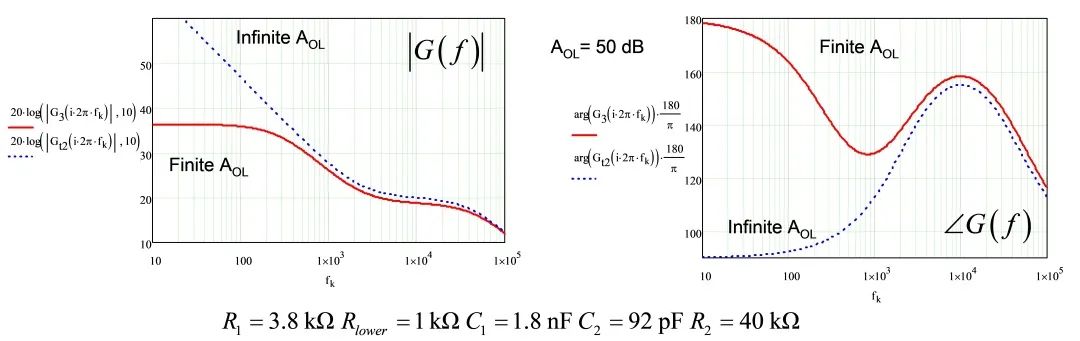
举例说明，我们对比理想的运放和开环增益为50dB的运放（例如TL431），此时补偿器必须满足以下目标：fc=10kHz和在此频率的增益补偿20dB，相位提升必须是65°。R1和Rlower计算用于12V输出和2.5V参考电压。（31）和（36）的两个动态响应如图10。交越增益和相位升压的偏差可忽略不计。   然而，在120赫兹频率时（31）的增益为35dB，（36）则为45dB。最后，有限的AOL的准静态增益仅36.4dB（»66），而无限时则为完美的运放。增益少两倍时，电源频率将影响控制系统的能力，抑制整流纹波。输出变量可能会受到此元件的影响，特别是在电压模式控制下。此外，若植入增益低，控制变量可能有显着的静态误差。若您现在选择具有更高AOL的运放如80dB，偏差消失，两曲线相互非常接近。  

图10：在type 2的波特图中，我们认为开环增益AOL和低边电阻Rlower并没有太大影响原完美的方程式。

05

总结

本文的前两篇，介绍一个补偿器采用一个非理想运放时开环增益的影响。假如运放不是完美的，您可看到动态响应中在低频范围内弱开环增益的影响，来评估这种情况导致的性能下降。