对称性和空间维度可对具有能隙的物态进行拓扑分类

半个世纪前固体能带理论的提出，让人们认识到材料为什么可以分为金属、绝缘体或者半导体，并促进了半导体产业的迅猛发展。现在人们认识到，系统的能带还可以根据对称性和空间维度，进行详细的拓扑分类。例如，考虑时间反演对称性、粒子-空穴对称性、手征对称性，以及不同的空间维度（d），绝缘态系统可以衍生出种类丰富的拓扑物态（见下表）。

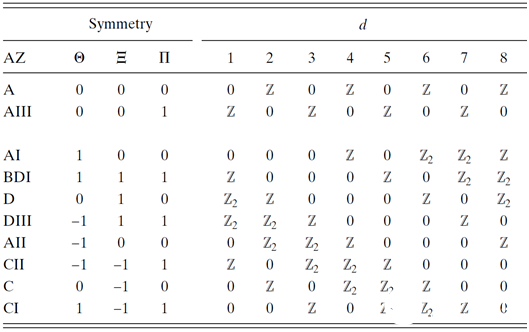
按照对称性和空间维度可对具有能隙的物态进行拓扑分类

拓扑材料具有拓扑保护的物理性质，不受杂质、缺陷等因素的影响，因而在低能耗、高速响应器件，量子计算等领域中具有巨大的潜在应用，在近十多年来受到了非常广泛的研究。人们已经在天然材料和人工材料中提出和验证了多种一维到三维的拓扑物态。例如，在破缺时间反演对称性（表中A类）的二维系统中，克劳斯·冯·克利青发现了整数量子霍尔态；在具备时间反演对称性的费米子系统中（表中AII类），人们发现了二维或者三维的拓扑绝缘态；考虑粒子-空穴对称性后可以出现一维到三维的拓扑超导态等。

我们生活的世界是三维空间，难以制备维度高于三维的材料系统，因此目前对高维度拓扑物态的研究还非常匮乏。

相比于天然材料，人工系统，特别是电路系统，具有若干优点。例如，系统的能带可以被精确设计和调控；系统具有自由的格点连通性，可以用来模拟任意维度的连接。因此，电路系统为实现有趣的高维拓扑物态提供了理想的实验平台。

近期，武汉大学余睿、南京大学赵宇心和斯图加特马克斯-普朗克研究所的Andreas Schnyder利用电路连接自由度高、不受空间维度制约的特性，用电容和电感器件构建了一个具有四维连接性质、满足经典时间反演对称的电路网络（如下图）。

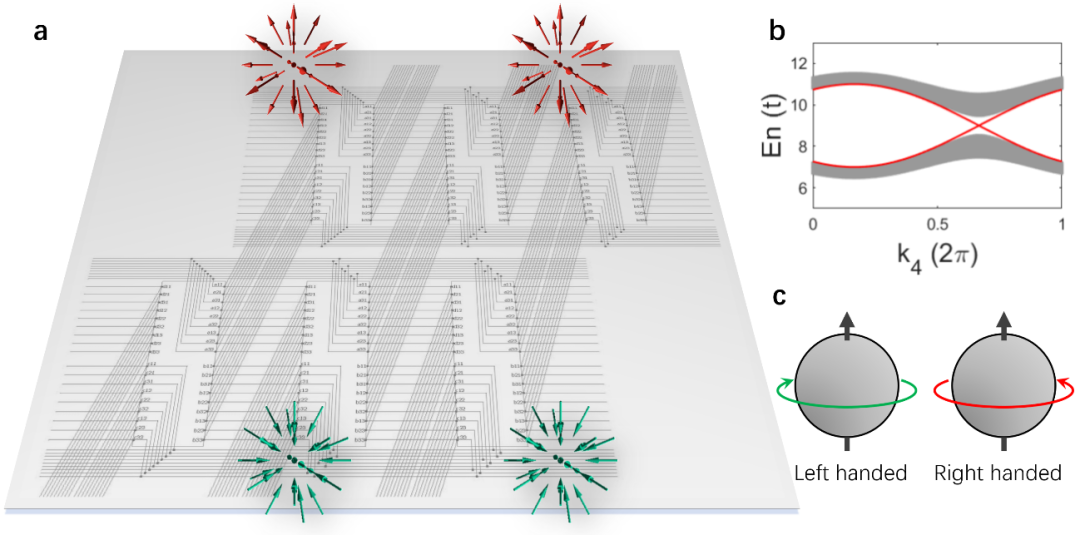
（a）四维电路投影到二维电路板上。其三维边界上可以存在一对手性相同的外尔点。（b）三维边界上体态（灰色部分）和外尔点的色散（红色部分）。（c） 外尔点手性示意图。

通过理论分析，研究者证明此系统属于上表中AI分类的四维拓扑绝缘态。拓扑绝缘体是一种很特殊的材料：系统体内绝缘，但表面因为存在拓扑保护的、无能隙的表面态而具备高度导电性。类似的，对于具有四维拓扑绝缘态性质的电路网络，其体内频谱具有能隙，但其三维表面上存在一对符合三维Weyl态特征的能隙闭合点（上图b）。

更重要的是，这种特殊的表面态起源于四维空间的拓扑数——第二陈数。拓扑数确定了Weyl态必须成对出现在边界上且具有相同的手征（上图a），即它们的内禀旋转自由度和传播方向遵循相同的左手或右手定则（上图c）。这些性质和低维材料中的表面态性质有很大不同。

研究人员通过电路仿真指出，这种四维拓扑态能够在电路板或集成电路晶圆上实现；系统表面的三维Weyl态的性质可通过电路节点电压表征和操控。

上述设计方案具有普适性，可用于实现任意维度的其它类型的拓扑物态，且这种方案具有实现简单、重构性强、可灵活控制等优点。研究人员期望该方案能够在拓扑相变、非线性效应、高维物态、非平衡现象以及开放量子系统（非厄密系统）的研究中起到重要作用。

该研究得到了科技部科研项目和国家自然科学基金的资助，相关成果发表于《国家科学评论》（National Science Review）。
       责任编辑:pj