

如何用电路证明傅立叶变换成立?
电子说
描述
自我感觉傅立叶变换和拉普拉斯变换很有趣,也很有用处就想和大家分享一下,由于是科普,我不打算用数学运算进行讲解,只拿大家身边的例子进行举例,大家可以简单看一下,粗略了解一下傅立叶变换及拉普拉斯变换是什么,如果感兴趣,可以看看奥本海姆的信号与系统。
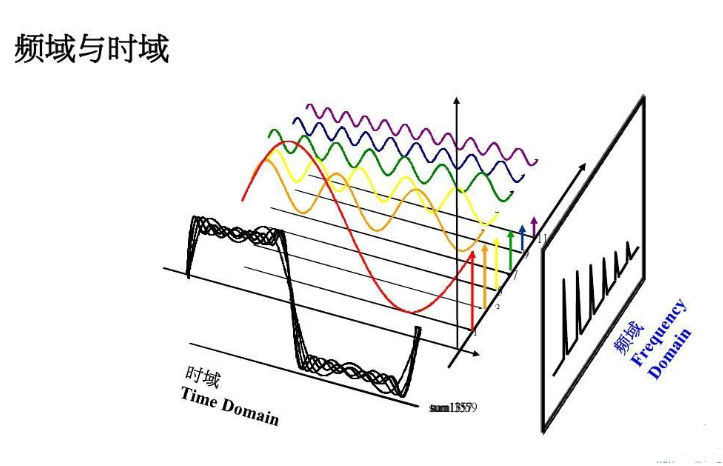
傅立叶认为任何信号都可以分解成无数个振幅不同,角频率不同的正弦波,因此提出了傅立叶变换,是时域到频域的一种变换。拿一首歌来举例,我们听到的声音就是时域,把这首歌用电脑录制下来将得到一连串的幅度随时间变化的波形,通过改变振幅可以改变这首歌的音量,但无法改变它的音调,因为音调是频域了,只能在谱曲时改变音符的方式进行改变。
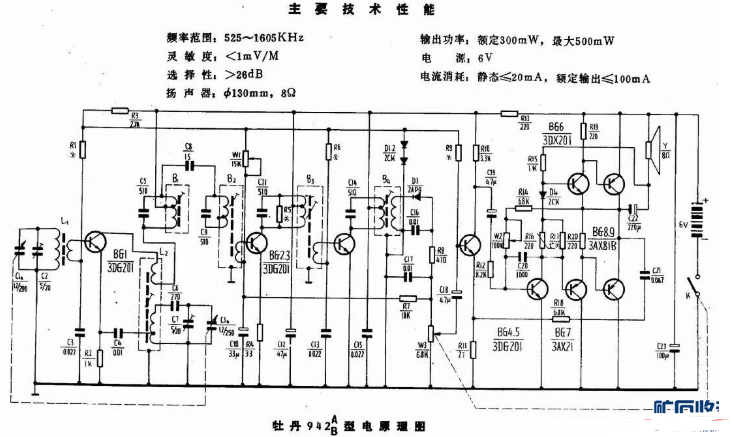
如何用电路证明傅立叶变换成立?图二是一个超外差收音机的电路图,在振荡电路中(振荡电路是一个引入正反馈的放大电路,只有输出端,通电就输出振荡信号),假设LC谐振频率为1MHz,那么它就会输出一个1MHz的正弦波振荡,为什么?此时不如分析一下工作原理:在通电瞬间,或由于电流瞬间冲击,或由于晶体管噪声,或由于外界干扰,VT1集电极所接的初级绕组中会有一个瞬间电流流过,根据法拉第电磁感应定律,初级绕组的电流变化会带来磁通量的变化,而磁通量的变化又会引起次级绕组(LC谐振电路)的电流变化,暂假设这个这个电流不能分解成无数振幅不同,角频率不同的正弦信号,则LC谐振电路就选择不出f=1MHz的频率,振荡就无法建立,电路就无法起振,可实际并非如此,这个电路确实可以起振,这就说明这个电流中有1MHz的频率,傅立叶变换成立。那么,傅立叶变换在生活中有什么应用?
乔碧萝奶奶的变声器就是一个例子,她的嗓音不可能那么甜,因为她的嗓音有很多谐波分量,此时把这些谐波分量去掉声音就纯净了。还有各种自拍软件的祛痘功能,图片是二维的,是亮度随时间变化的函数,反映脸型的肯定是低频频率,反映眼睛鼻子耳朵的肯定是较高的频率,那么反映连上细小缺陷都肯定是非常高的频率,把这个频率去除,就可以拿去照骗了。当然了,傅立叶变换在生活中还有很多我就不举了。
但傅立叶变换实际上有一个局限性,就是要求这个信号绝对可积,可实际上很多信号都不满足这一条件,于是拉普拉斯就说了,你将原时域函数乘上一个与 σ相关的衰减因子,不就行了吗?这就是拉普拉斯变换,所以傅立叶变换可以看做拉普拉斯变换的特殊形式,傅立叶变换就是 σ为0时的拉普拉斯变换,这就是二者的互通性。
另一个角度来看,傅立叶变换是将时域的函数变换到频域,即ω域。 拉普拉斯变换是推广到了复频域,即s域。 如果这个复数的实部为0,那么就回到单纯的频域。
-
傅立叶变换的条件的理解2023-09-07 8704
-
信号经过傅立叶变换所得频谱的物理意义讨论2022-11-25 2771
-
图像傅立叶变换的物理意义2022-06-06 3997
-
傅立叶变换是怎么变换的 傅立叶的理解2021-08-25 6075
-
简述FPGA的快速傅立叶变换2021-05-27 2742
-
labview短时傅立叶变换2020-06-13 3186
-
了解小波变换针对傅立叶变换的优点2020-05-07 6276
-
进行傅立叶变换的原因、定义、物理意义简述2018-04-06 24760
-
基于分数阶傅立叶变换的ARM检测技术2017-09-24 912
-
信号处理中的傅立叶变换2015-12-30 693
-
周期信号的傅立叶变换.ppt2009-09-16 813
-
傅立叶变换.ppt2009-08-26 831
全部0条评论

快来发表一下你的评论吧 !

