区块链干货：关于钱包的基础密码学

通过区块链，人类历史上首次通过技术彻底、纯粹地保障「私有财产神圣不可侵犯」。

让人沉思，让人兴奋的一段话。

可在这背后的基础技术「密码学」是如何工作，以及保障数字资产的安全呢？无论你是爱好者亦或投资客，应该需要多少了解背后的原理，免得误解，轻则闹笑话，重则损失资产。因为我们总会听到一些鬼扯的故事（帮我找回密码吧！私钥发到群里了诶！），皆是由于对钱包本质的不了解。

本文仅谈论钱包原型涉及的相关密码学，不包含 keystore，助记词，转账交易等。

钱包如何生成

这是以太坊黄皮书关于钱包（私钥、公钥、地址）的描述，仅仅 2 行文字。主要讲解私钥通过 ECDSA（椭圆曲线签名算法）推导出公钥，继而经过 Keccak 单向散列函数推导出地址。

分解为 3 个步骤：

1. 创建随机私钥 （64 位 16 进制字符 / 256 比特 / 32 字节）

2. 从私钥推导出公钥 （128 位 16 进制字符 / 512 比特 / 64 字节）

3. 从公钥推导出地址 （40 位 16 进制字符 / 160 比特 / 20 字节）

这是我从 ethereumjs/keythereum 中剥离出来的 JavaScript 代码，关于黄皮书上的公式的具体实现，仅仅 6 行代码。

这是一件很奇妙的事情，2 行文字，6 行代码承载着亿万级别的资产，但往往越简单，越奥妙。以上的 6 行代码，就已经囊括密码学中大多数技术，比如随机数生成器、非对称加密，单向散列函数等。以下我会为大家解剖这 6 行代码，逐一介绍背后相关的密码学知识。

随机数

随机数用于生成私钥，若随机数可以被预测或重现，则私钥就会立刻形同虚设。所以保证随机数拥有下列三项特征，至关重要：

随机性：不存在统计学偏差，完全杂乱的数列

不可预测性：不能从过去的数列推测下一个出现的数

不可重现性：除非将数列保存下来，否则不能重现相同的数列

软件本身是无法生成具有不可重现性的随机数，因为运行软件的计算机本身仅具备有限的内部状态。所以通过确定性的代码，在周期足够长的情况下，必然会出现相同的随机数。因此要生成具备不可重现性的随机数，需要从不确定的物理现象中获取信息，比如周围温度、环境噪音、鼠标移动，键盘输入间隔等。

在 Linux 内核中维护了一个熵池用来收集来自设备驱动程序和其它来源的环境噪音。熵（entropy）是描述系统混乱无序程度的物理量，一个系统的熵越大则说明该系统的有序性越差，即不确定性越大。

所以在选择生成私钥的随机数方法时，需要选择满足密码学强度的随机数方法，比如 Node 中的 crypto.randomBytes。当你调用 crypto.randomBytes（32） 方法时，它会等待熵池搜集足够的信息后，返回 64 位的随机数，即私钥。

另外，在以太坊中想要获得随机数是一件不容易的事情，因为矿工需要得到同样的结果，并经过验证提交到区块链上。但如果 EVM 存在 random opcode，矿工会生成不一致随机数，无法达成共识。

目前社区也提出相应的方案，Mist 的作者 Alex van de Sande 提出使用 blockhashes 生成随机数，但由于矿工拥有操纵区块数据的能力，如果有能力且愿意放弃 5 个区块的奖励，理论上可以间接影响随机数，所以不是完全足够安全可靠。

为了解决矿工有可能作恶的问题，国内社区提出 RANDAO： A DAO working as RNG of Ethereum 项目，构建一个人人可以参与的 DAO，通过经济激励，由所有参与者共同决定一个随机数。在 RANDAO 的基础上，Vitalik Buterin 也提出 RANDAO++ 方案，感兴趣可以看看。

非对称加密

在对称密码中，由于加密和解密的密钥相同，所以必须向接收者配送密钥用于解密。但发送密钥过程中，窃听者可以窃取密钥解密，不发送密钥吧，接收者无法解密，密钥必须发送，但又不能发送，这问题称为密钥配送问题。一般采取事先共享密钥、密钥分配中心、Diffie-Hellman 密钥交换等方案来解决，但直到非对称加密方案的出现，无需向接收者配送解密密钥，密钥配送问题才完美解决。

在非对称加密中，将密钥分为加密密钥和解密密钥，也就是我们常说的公钥和私钥。公钥和私钥一一对应，由公钥加密的密文，必须使用公钥配对的私钥才可以解密。

看似有点复杂，我们祭出密码学的男女主角 Alice 和 Bob，来通俗地梳理一下：

发送者： Bob，接收者：Alice，窃听者：Eve

1. Alice 生成密钥对（私钥和公钥），私钥由 Alice 自身妥善保管

2. Alice 将自己的公钥发送给 Bob，即使被 Eve 窃取也没关系

3. Bob 使用 Alice 的公钥对消息加密，发送给 Alice

4. 密文可能被 Eve 窃取，但他无法使用公钥解密

5. Alice 使用自己的私钥解密密文

当我们调用 secp256k1.publicKeyCreate 获得公钥时，实际使用的是非对称加密中的椭圆曲线算法。通过该算法可以从私钥推导出公钥，这是一个不可逆的过程：K = k * G。给出常数点 G 时，使用已知私钥 k 求公钥 K 的问题并不困难，但反过来，已知公钥 K 求私钥 k，则非常困难。这就是椭圆曲线算法上的离散对数问题，也是为什么你可以分享地址（或公钥）给别人，但不能暴露自己的私钥。

const publicKey = secp256k1.publicKeyCreate（privateKey， false）.slice（1）

// publicKey.toString（‘hex’）： 1e3f1532e3285b02.。.45d91a36a8d78cb6bef8

为了形象的表现椭圆曲线算法如何将私钥推导出公钥，我们将使用简单的整数作为私钥 k，找到公钥 K = k * G，也就是 G 相加 k 次（数学原理一致）。在椭圆曲线中， 点的相加等同于从该点画切线找到与曲线相交的另⼀点， 然后映射到 x 轴。下图展示了从曲线上获得 G、2G、4G、8G 的几何操作。

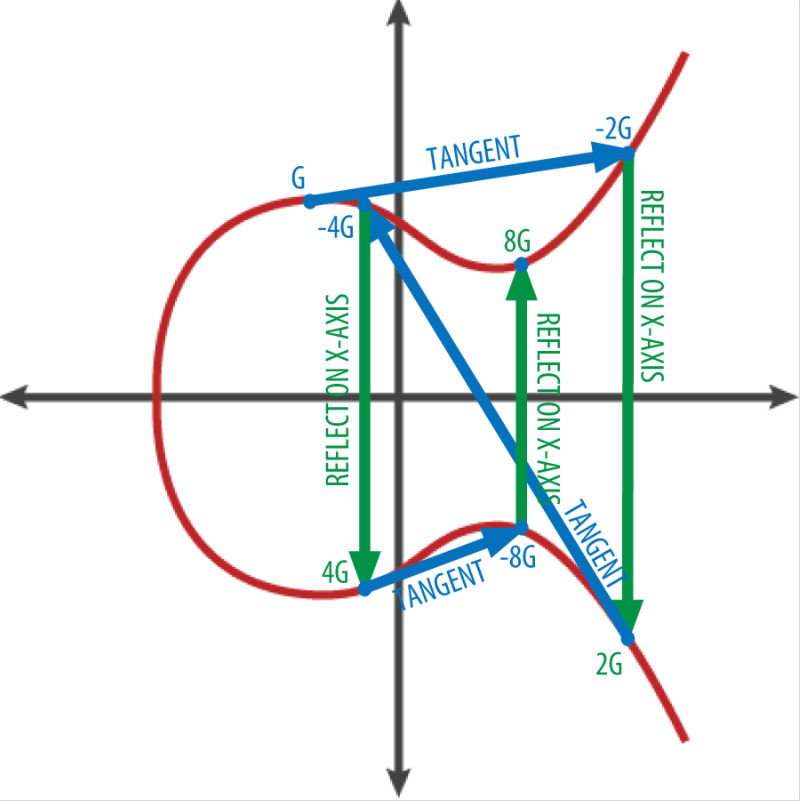
单向散列函数

单向散列函数 （one-way hash function） 有一个输入和一个输出，其中输入称为消息 （message） ，输出称为散列值 （hash value） 。散列值也称为消息摘要 （message digest） 或者指纹 （fingerprint） 。单向散列函数可以根据消息的内容计算出散列值，而散列值就可以用来检查消息的完整性。

单向散列函数拥有下列四项特征：

1. 根据任意长度的消息计算出固定长度的散列值

2. 能够快速计算出散列值

3. 具备单向性

4. 消息不同散列值也不同

当我们调用 createKeccakHash（“keccak256”） 方法时，Keccak 使用海绵函数，对公钥与初始的内部状态做 XOR 运算得到 32 字节散列值，取其后 20 字节，转成 40 位的 16 进制字符，即为地址。

在以太坊中还有许多地方应用了单向散列函数，例如：

1. 矿工需要不断计算特定数据的散列值，当散列值满足难度要求时，矿工便可以广播该区块，获得奖励。

2. 根据默克尔树根哈希的值前后是否一致来判断区块中的交易是否被篡改

题外话，有一阵子我很好奇单向散列函数或哈希函数中的 ”Hash“ 代表什么意思呢？后来经过查询得知， ”Hash“ 在古法语中的原意时「斧头」，后来被引申为「剁碎」，正好形象的比喻单向散列函数，将消息剁碎，混合成固定长度的散列值。后来通过 Herbert Hellerman 的《Digital Computer System Principles》成为广为流传的术语。