研究微分系统的整体性质及其在扰动中的变化

微分在数学中的定义：由函数B=f（A），得到A、B两个数集，在A中当dx靠近自己时，函数在dx处的极限叫作函数在dx处的微分，微分的中心思想是无穷分割。微分是函数改变量的线性主要部分。微积分的基本概念之一。

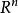设f是从欧几里得空间（或者任意一个内积空间）中的一个开集射到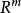的一个函数。对于中的一点x及其在中的邻域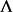中的点x+h。如果存在线性映射A使得对任意这样的x+h，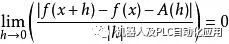

那么称函数f在点x处可微。线性映射A叫做f在点x处的微分，记作。

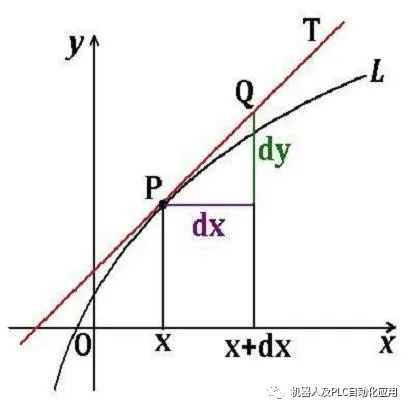
如果f在点x处可微，那么它在该点处一定连续，而且在该点的微分只有一个。为了和偏导数区别，多元函数的微分也叫做全微分或全导数［2］。

当函数在某个区域的每一点x都有微分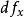时，可以考虑将x映射到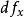的函数：

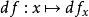
这个函数一般称为

微分函数

微分系统是系统科学的一个数学分支。主要研究随时间演变的微分系统的整体性质及其在扰动中的变化。

微分控制，即D控制，是指以微分为控制规律的控制过程和方法。基本控制规律有比例P、微分D、积分I三种。

D控制能够在早期修正信号，增加系统的阻尼程度，改善系统稳定性，但对稳态性能没有影响，且对噪音敏感，容易出现过操作。

微分控制是对输入量的变化量进行反应的，也就是说，D控制不对输入量本身有反应，而仅对输入量的变化有反应。基于这个特点，微分控制的优缺点也十分明显。

微分控制的优点是，能够敏感感知输入量的波动，使控制器尽早做出反应，增加了系统的阻尼程度，提高了系统的响应速度，提高了系统的动态性能。用于串联校正时，实际上使系统增加了一个开环零点，使系统的相角裕度提高。

微分控制的缺点是，若系统的输入量不变，即使输入量和输出量之间存在偏差，微分控制也无法作用；同时，若出现了变化率很大的噪声，微分控制会有过度的反应，影响控制器的工作。

因此，微分控制仅对动态过程起作用，对稳态过程没有影响，且对系统噪声敏感，一般不会使用单独的D控制。
        责任编辑:pj