

一文详谈伊辛模型:描述物质的铁磁性
电子说
描述
100年前,一个名叫恩斯特·伊辛(Ernst Ising)的物理学家提出了一个模型,称为伊辛模型。这个模型是作为一种犹如卡通图景提出的,用于描述物质的铁磁性,如下图片所示。
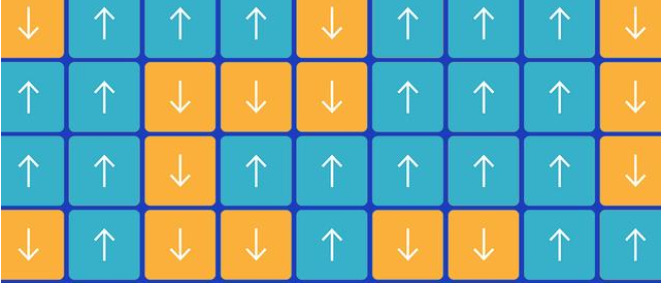
1920年,在一个从当时全球流感大流行中恢复过来的世界中,一位名叫威廉·伦茨(Wilhelm Lenz)的德国物理学家,着手理解为什么加热磁铁超过一定温度会导致其突然失去吸引力,就像著名的物理学家皮埃尔·居里(Pierre Curie)在当时25年前就发现的那样。
伦茨将一块磁铁想象成一个如上面动画所示的小箭头的格子,每个箭头指向上方或下方,代表原子。原子本质上是磁性的,具有北极和南极,因此可以认为它们具有方向。箭头会影响它们的邻居,并试图磁性翻转它们以匹配其自身的方向。
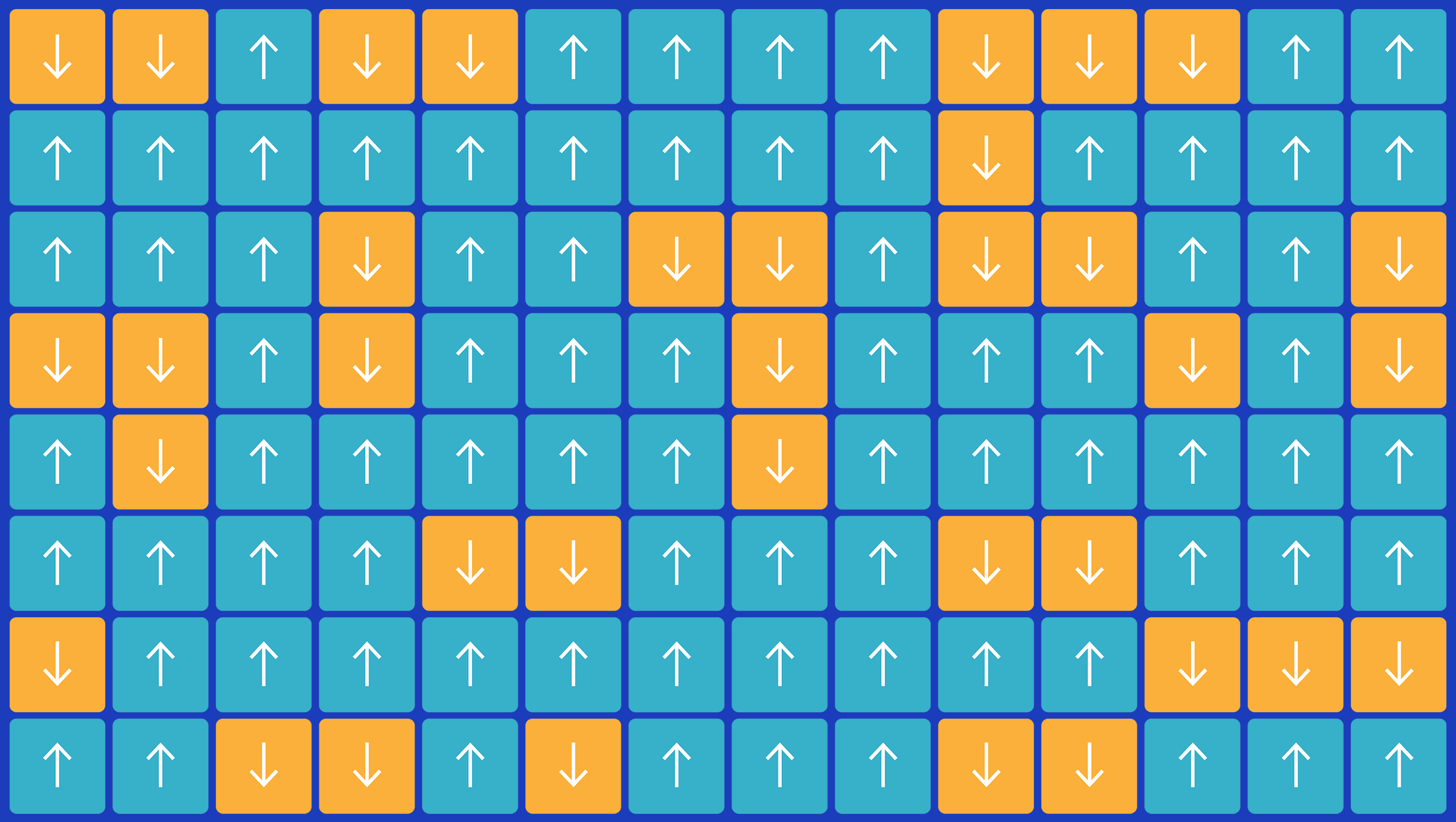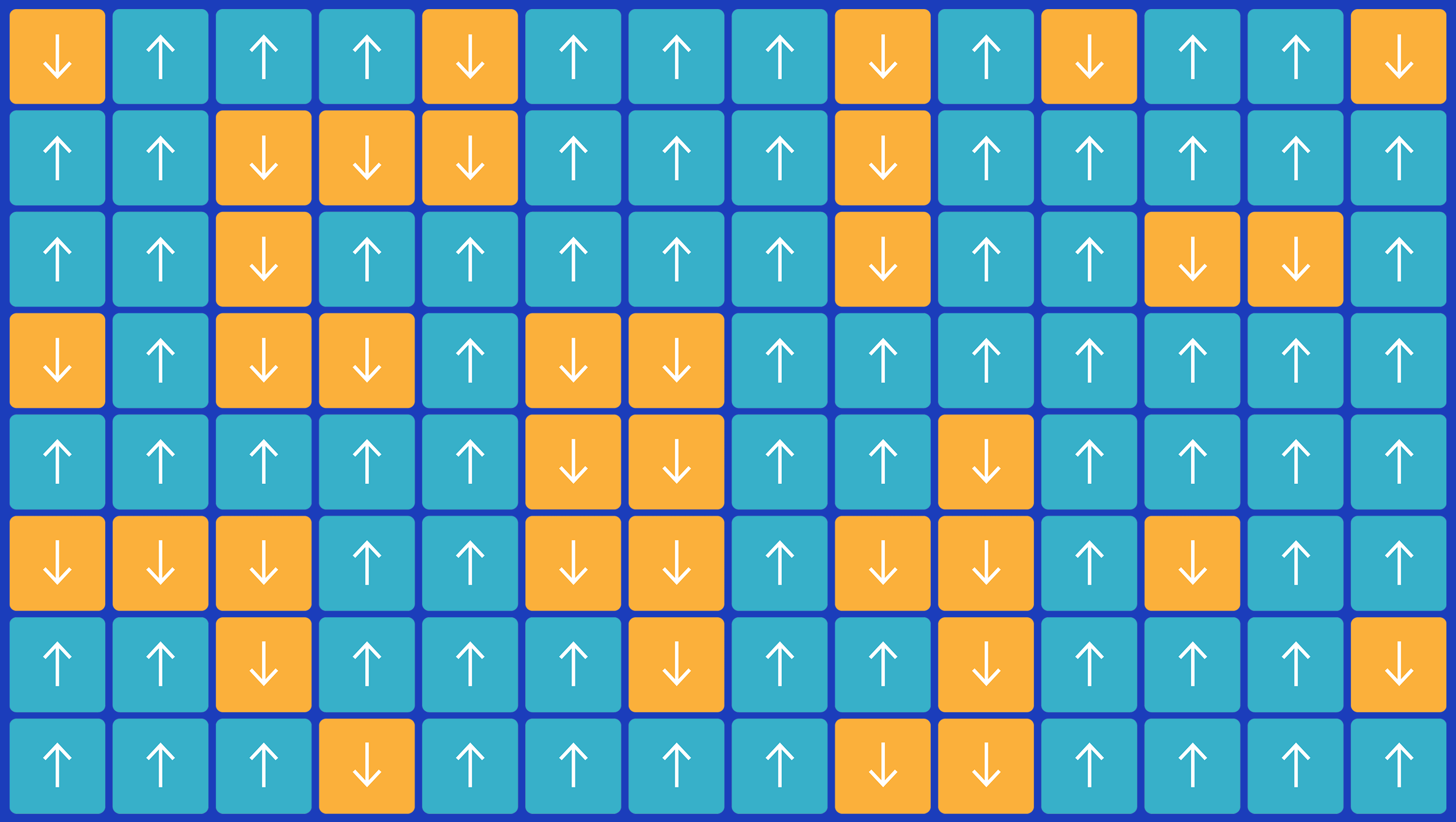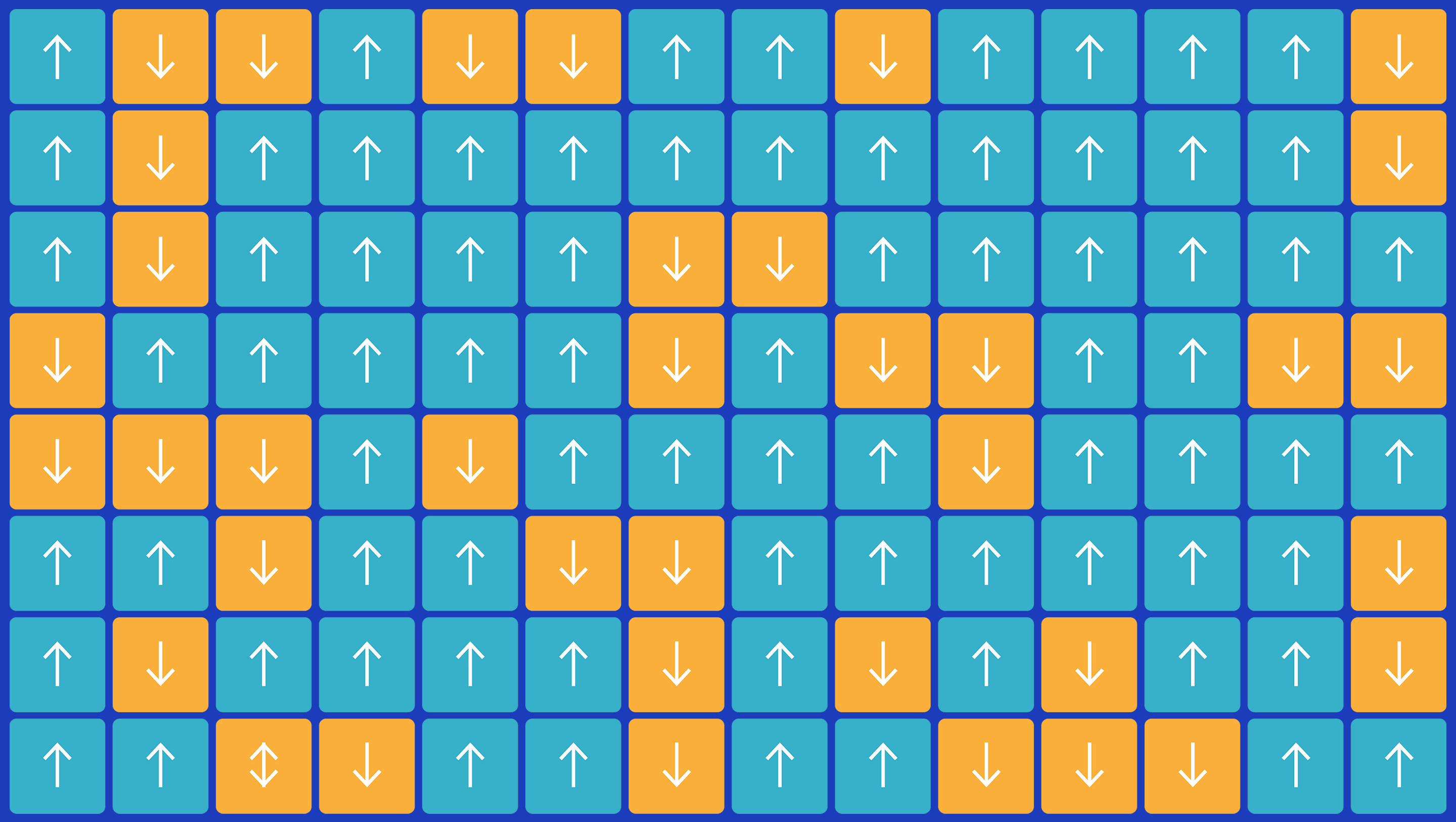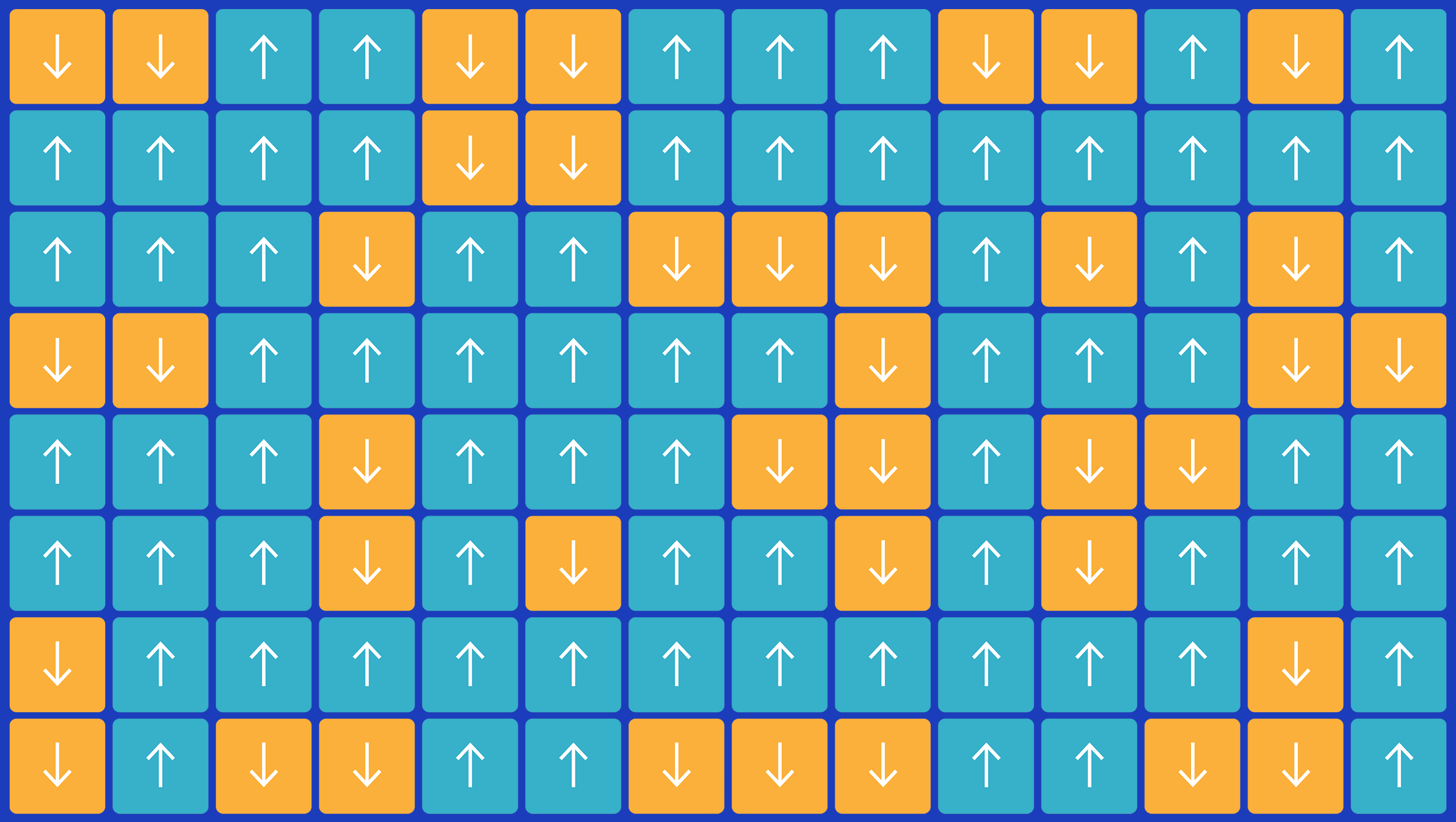
伦茨指出,如果大多数原子指向一起,它们的微小磁场将会融合,并且整个材料的作用就像一块磁铁。但是,如果“向上”原子与“向下”原子均匀混合,它们将被中和,而不会出现大范围的磁性。
为此已经发表有数千篇物理学论文,一直在尽力理解这种晶格内的热与磁之间的特征。热量,代表的是颗粒的随机而无序晃动;然而磁性却与这种混乱相违抗。伦茨认为,在低温下磁性的有序应该会获胜。然而,有了足够的热量,随机撞击将破坏原子的合作,这解释了居里的观察,即热磁铁失去了磁的魔力。
为此伦茨委托其研究生恩斯特·伊辛(Ernst Ising)具体深入研究。实际上磁体是三维的,但伊辛将此研究课题简化为线性的箭头链,每个箭头都可以感知其两个最近的邻居。伊辛在他一篇1924年的论文中求得了一维线性箭头链的伊辛模型的解析解。他和伦茨假定结果同样适用于二维平面箭头和三维立体箭头,结果该模型无法捕获真实磁体的行为。这个理论似乎走到了一个死胡同被搁置在了一边。
尽管如此,伊辛模型还是由于数学上的新奇而幸存下来。直到1940年代,它引起了理论物理学家和最终的诺贝尔奖获得者拉斯·昂萨格(Lars Onsager)的注意。昂萨格努力解决二维情况下的伊辛模型,即计算在任何给定温度下可能指向“向上”的原子的比例,其中每个二维箭头不是临近有两个而是有四个邻居。
无论解决一维还是二维这两种情况,都需要考虑每个箭头对其它每个箭头的影响,比如邻居的邻居的邻居等的无限地作用于每个邻居的间接影响力会出现。在二维平面情况下,这种情况远比一维线性复杂得多。昂萨格于1944年发布了他的解决方案。计算机科学家索林·伊斯特拉伊(Sorin Istrail)评价说,这一解决方案代表了一项“非人类”的数学工作——至今仍难以理解。“当您一步一步地沿着这个方案走下去,除了证明是正确的以外,在证明的末尾也什么也没有。”
昂萨格的证明表明,就像伦茨所怀疑的那样,在二维模式下,箭头在低温下对齐并且磁场保持着状态,而在系统超过“临界温度”后,无序状态就出现了。互连的箭头的简单网格说明了相变。就像许多物理学家所认为的那样,不需要合并真实粒子的混乱。
看来,模型仍然似乎简化得太多,得到了现实的嘲弄。丹麦罗斯基勒大学的物理学史学家马丁·尼斯(Martin Niss)评价说:“这样的模型看起来仍有点可疑。”
在昂萨格解决方案之后,杨振宁和李政道研究了温度接近临界温度时分配函数变得奇异的方式指出:在统计力学和统计场论中,有些铁磁配分函数的零点都是虚数,而取名为杨-李定理。
伊辛模型的状况直到科学家努力测量氩气和氦气后,一切都改变了,表明昂萨格的解决方案抓住了这些物质的“关键指数”。这些指数,如1/8和7/4之类的数字,描述了从预热到相变的各种特性,例如热容量变化的速度。尼斯指出,到1965年,大多数物理学家已经了解了伦茨和伊辛的箭头,尽管仍不清楚物理上不现实的图景是如何抓住这些具体细节的。
问题的答案不在于模型,而在于自然。伊辛模型之所以强大,是因为一系列无关的物质以相同的临界指数转化,这种现象现在称为普遍性。
美国物理学家肯·威尔逊(Ken Wilson)于1971年制定了通用性数学,并因此获得了诺贝尔奖。威尔逊表明,尽管在高温下箭头指向了它们喜欢的任何方向,但随着系统冷却并接近其相变,相邻点之间的磁引力会形成越来越大的有序“孤岛”,所有箭头都指向一起。关键指数描述了这一过程的细节,例如最大的岛如何成长。
如图所示包含所有大小的黑白区域的网格,当伊辛模型处于临界温度时,它包含所有大小的对齐箭头的“岛”。

在临界温度下,从点到片,各种大小的岛共存。在这里,一个箭头可以翻转另一条遥远的箭头,尽管它们并不是相邻的箭头,这表明该系统的宏观特性已经脱离了其微观细节。这种超脱是普遍性的魔力。具有相同数量的尺寸和相同的对称性的所有系统都会经历相同的相变,无论其微观部分是铁原子、水分子还是小箭头。
普遍性意味着,只要研究人员想要了解具有许多相互作用的实体的情况,并可以用相反的标签,例如“上”和“下”或“存在”和“不存在”等来描述,那么他们可能会从伊辛开始。加州大学伯克利分校的凝聚态物理学家弗朗西斯·赫尔曼(Frances Hellman)说:“有一种方法可以使伊辛模型成为最简单的可解模型。” “但这使您有很长的路要走。”研究人员还可以比如通过使箭头在平面中自由旋转来扩展模型以适合其他物理系统。
但是,即使伊辛模型改变了物理学家对材料的理解,研究人员仍在努力解决三维版本的难题,即找到一个清晰的公式,以了解在任何给定温度下三维箭头晶格如何磁化。甚至著名理论物理学家理查德·费曼(Richard Feynman)都未能完成伊辛最初的1920年所提出的任务。
如今,计算机可以模拟三维伊辛模型,并以合理的精确度逼近其关键指数,因此没有紧迫性来寻找确切的解决方案,然而渴望仍然存在。物理学家的一项合作于2012年宣布,在探索逻辑上可能的物理学理论的空间,即每个点与一组关键指数匹配时,他们确定了一个包含三维伊辛模型的确切关键指数的区域。此后,该小组进一步缩小了该区域。在12月,他们运用其方法解释了1992年航天飞机飞行中令人费解的液氦测量结果。
参与这项工作的法国高等科学研究院的物理学家拉瓦·里奇科夫(Slava Rychkov)说,要弄清楚三维关键指数的其他小数位是不可能的。在其可能的物理理论图上的其他地方,存在伊辛扩展,带有奇异粒子的奇异宇宙理论,甚至可能是真实宇宙中难以捉摸的引力量子理论。 伊辛模型表示此抽象“理论空间”中最简单的位置之一,因此可以作为开发探索未知领域的新颖工具的试验场。
里奇科夫说,如果能够精确确定其关键指数的确切值,“它将通过某种完全未知、然而全新的解决方法来实现”。 “这必将是一场革命。”
据报道,中国科学院金属研究所研究员张志东推定出三维伊辛模型的精确解。至今尚待得到国外学术界的一致认可。
可以肯定的是,伊辛模型代表了有序和无序的自然界普遍存在的两种状态,两个状态转变之间存在一个临界点,临界点附近有许多有趣的临界现象。
这样的两个状态的转变现象是普遍性的,铁磁材料从顺磁态到铁磁态的转变,超导体从正常态到超导态的转变,水以及许多液体材料的液态与气态,甚至生物体中DNA的折叠、病毒的传播、人工智能体系的计算、大脑神经细胞的激活与不激活状态等,都存在着有序和无序的相变和临界现象。
伊辛模型,描述的就是临界现象的一个基本模型,它考虑每一个自旋有两种可能的状态,自旋和自旋之间存在相互作用。这一模型可被推广用于研究连续的量子相变、基本粒子的超弦理论、动力学临界行为等,以致可以描述森林火灾、交通堵塞、股市涨落、舆情传播等社会经济现象。
伊辛模型提出一百年来,其应用范围已经远远超出了当初的磁性的简单模型描述,扩展应用到理解从磁铁到大脑的许多方面,影响与改变着科学。
-
一种检测润滑油中铁磁性磨粒的仪器2009-07-18 640
-
一种基于检索频度的网格资源描述模型2009-09-03 423
-
铁磁性钢丝绳电磁检测方法2010-03-30 1212
-
磁性材料2009-04-10 2466
-
磁性元件内部资料2011-06-14 1157
-
如何制作一个没有磁性的指南针?2018-08-03 15760
-
磁控溅射铁磁性靶材的主要方法2019-04-29 10005
-
一文详谈波峰焊接工艺资料下载2021-04-29 1276
-
具二维亚铁磁性石墨烯系统首次合成2022-12-21 717
-
铁磁性材料的性能以及分类2023-02-13 16965
-
首次实现二维氮化物基宽禁带半导体的室温铁磁性2023-02-22 1311
-
一文了解如何应用QUBO模型来建模2023-04-06 20609
-
磁性材料在新能源汽车中的应用2023-07-26 2487
-
铁磁性的概念、产生机理、应用2024-12-06 4919
-
永磁电机中磁性材料的选择2025-11-11 395
全部0条评论

快来发表一下你的评论吧 !

