

基于分裂式ADC的LMS算法实现数字后台校正
模拟技术
描述
引言
模数转换器(ADC)是连接模拟世界与数字世界的桥梁,在纳米工艺节点下,SAR ADC具有功耗低、结构简单、易集成等特点成为研究热点。但由于工艺误差,电容的匹配精度难以高于0.1%,成为影响ADC线性度的主要因素。
为了消除电容间的失配,除了较好的电容阵列版图之外,还需要对电容进行校正。校正方式包括数字校正与模拟校正。数字校正是指电容失配的消除在数字域完成,每一个电容的权重都对应一个数字码字。校正的目的是让数字权重逼近电容制造完成后在总电容阵列中所占的比重(即真实权重),从而消除电容失配。数字后台校正是指没有特定的校正模式,校正的过程完全在后台自动进行。
由于电容校正的应用十分广泛,在不同应用场景下对于校正方式与要求也不同,国内外很多人对此进行了研究。文献[1]采用了模拟域校正方法来消除非线性,但是额外的模拟模块会增加电路的噪声并增加硬件复杂性,且模拟电路不会随着工艺的进步带来性能的显著提高。文献[2]提出了一种数字校正方法,但是在前台进行的,校正工作时需将正常采样过程停止,且校正系数不能随外部环境变化更新可能导致不准确。文献[3]提出了一种数字后台校正技术通过将伪随机噪声注入到输入中,但是减小了输入信号范围。
针对上述问题,本文提出了一种Vcm-based SAR ADC的数字后台校正方法,通过对输出码字在数字域的处理来补偿模拟域的非理想特性。校正过程在后台进行,不影响ADC的正常采样和量化。文章第2节主要描述该方法的工作原理及流程;第3节给出仿真结果;第4节给出最终结论。
1、 数字后台校正方法原理
LMS(Least Mean Square,最小均方)算法来源于自适应滤波器的设计,但也可以应用在ADC的数字校正中。一种方案是提供一个输出所要趋近的理想信号d(n),一般是由精确的参考ADC提供,如单斜式ADC或Σ-ΔADC,其精度较高但采样率较低。因此参考ADC的采样频率为主ADC的L分之一,即主ADC在L次采样后才能进行一次迭代计算。
这种基于参考ADC的LMS校正算法增加了电路的面积、功耗、以及复杂度,一种改进的方案是采用分裂式ADC的LMS算法。即把原来的ADC分为两个结构相同的ADC,电容值减半,两个子ADC同时对输入信号进行采样和量化,输出的平均值作为系统最终的输出。虽然电容值减半噪声会随之加倍,但平均操作也会使噪声减半,因此噪声和功耗相比原ADC不会增加。
当一个N位的ADC在量化结束后,输入信号模拟值可表示为:

式中, D i 代表每一位量化后的码字, ω i 为该位对应的权重值,V REF 为电容阵列的参考电压。当电容没有失配时, ω i 组成一组二进制权重序列,如果不考虑其他非理想因素, D i 就是输入信号 V in 正确的量化后的码字。但由于电容在制造过程中存在随机失配,权重 ω i不再是二进制权重序列,非理想的权重序列会导致量化码字出错,从而无法还原出真实的模拟输入信号。
采用分裂式ADC的框架图示意图如图2.1所示。
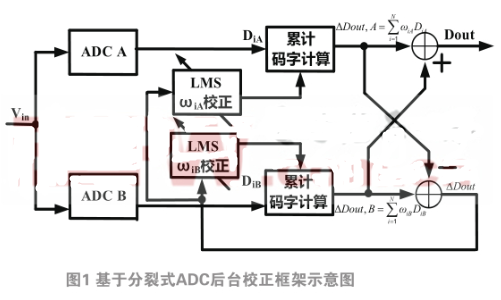
图中分裂式SAR ADC包括两个ADC子模块,每个ADC模块中DAC电容阵列采用非二进制编码电容阵列,两个ADC分别对同一输入信号进行采样和量化,它们的失配情况互不相同。
假设分别的实际权重为 ω iA 和 ω iB ,则输入信号可分别表示为:
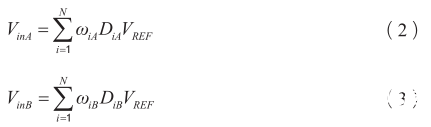
如果将实际权重表示为理想权重 ω i,ideal和误差权重ξ i 的和,则:

因此可以根据两个ADC量化后输出的码字将输入信号重写为:
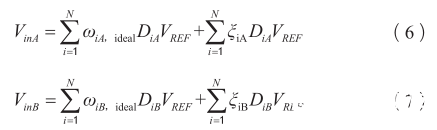
因为两个ADC是对同一个模拟输入信号进行采样和量化,在不断迭代权重更新后,量化码字D iA 和D iB 会趋于相等,所以量化后的输入模拟差值可表示为;
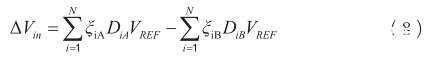
如果差值为零,则权重 ω iA 和 ω iB 就是真实的权重,所得到的量化后的模拟值也是正确的,权重的迭代可以表示为:

其中 μ 为LMS的迭代系数,控制着迭代的速度与精度,一般取2的指数次方。较大的值能使权重更快逼近实际权重,但是容易受到系统噪声的干扰,可能出现迭代错误。较小的值可以得到更精确的权重值,但是需要更多迭代次数,因此需要在速度与精度之间折中考虑。
综上所述,本文提出的电容阵列如图2.2所示。为了简化这里只画出单端示意图,另一端与此相同。
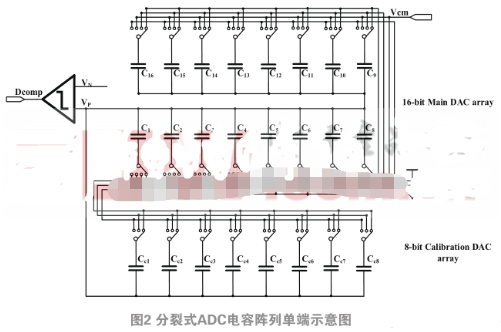
图中电容阵列包括16位主DAC电容阵列与8位辅助校正DAC电容阵列,采样方式为电容下级板采样,电容上级板均接在比较器的P输入端。主DAC电容阵列按高位到低位的顺序C 1 ~C 16 的电容值分别为5223C、5223C、5223C、2735C、1432C、750C、393C、206C、108C、57C、30C、16C、8C、4C、2C、1C,其中C为单位电容。辅助DAC同样按照高位到低位的顺序C C1 ~C C8 的电容值分别为8192C、4096C、360C、188C、98C、51C、27C、14C。
基于分裂式ADC的校正算法中两个ADC的工作模式不能完全相同,否则当电容失配方向一致时,码字误差始终为零,无法被校正。为了改变ADC的工作模式,这里通过辅助校正DAC向主DAC注入了一个随机偏移量,从而改变ADC的量化轨迹,提升ADC的线性度和动态范围。同时电容阵列为非二进制编码,引入了冗余量,可以弱化系统在量化过程中引入的动态误差,保证了DAC失配误差校正的可行性。
输入信号同时经过两个子ADC模块采样,采样结束后DAC电容上级板电压可表示为:
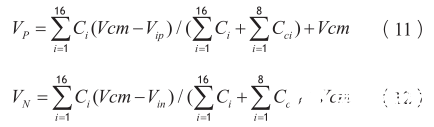
由于SAR ADC的第一次比较结果只与采样值有关,电容还没有开始切换,这样会导致两个ADC最高位的电容会朝着一个方向切换,因此就无法被校正。这里需要对最高位电容的切换进行单独处理,具体流程如下所述。
采样结束后首先随机切换辅助校正DAC电容阵列最高位电容C C1 ,由于ADC为双端电容阵列,比较器的两个输入端分别连接了DAC电容阵列,因此P端往上切,N端往下切,即P端连接的DAC电容阵列的最高位电容下极板从共模电压切换到更高的电源电压,N端连接的DAC电容阵列的最高位电容下极板从共模电压切换到更低的地电压。因此切换后N端上级板电压小于P端上级板电压,DAC电容阵列的上级板电压变化如图2.3所示。
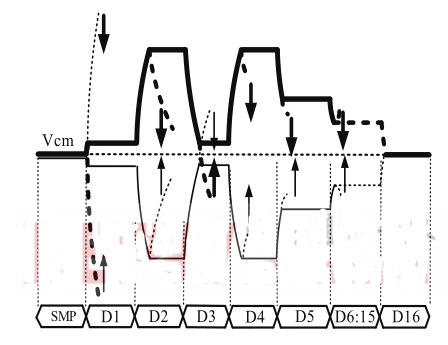
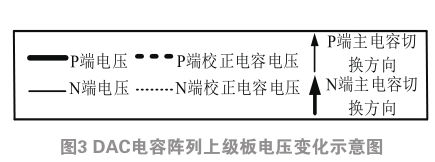
由于P端电压大于N端,因此第二次比较器比较结束后,P端主DAC电容阵列的最高位电容C 1 下极板会从V cm 接到低电位地,N端电容C 1 下极板会从V cm 接到高电位V REF ,同时PN两端的辅助电容阵列次高位电容CC2 继续朝相反方向随机切换。
假设第二次电容切换后P端电压仍大于N端电压,在第三次比较结束后,P端主DAC电容阵列的次高位电容C 2 下极板会从 V cm 接到低电位地。N端电容C2 下极板会从 V cm 接到高电位V REF ,同时PN两端的辅助电容阵列次电容C C3 继续朝相反方向随机切换。即主DAC电容阵列的切换一定是朝着V cm 的方向进行,而辅助DAC电容阵列的切换一直都是随机并且PN两端朝着相反的方向切换。
以此类推,直到8次比较以后,辅助DAC电容阵列下极板均连接 V cm ,主DAC电容阵列剩下还未切换的电容按着 V cm -based切换方式进行切换,最终得到两个ADC分别量化产生的不同的16位码字 D iA 和 D iB 。将两个输出码字 D iA 与 D iB 的差值作为误差信号连接到LMS ω iB 模块与LMS模块并按照公式2-9与公式2-10进行一次迭代处理。初始权重为设计电容值对应的二进制序列,迭代系数值取2 -16 。通过每次量化结束后的不断迭代,直到最终输出码字D out 的线性度达到要求,即可认为接近实际电容值,消除了电容间的失配。
2、 仿真结果
基于第2节的原理介绍,在MATLAB仿真环境中进行了行为级验证,证明了本方法可以有效地消除ADC中电容之间的失配,图3.1与图3.2为一个16位的SAR ADC经过数字后台校正后的结果,单位电容给3%的失配大小,在无校正的情况下有效位数(ENOB)为12.1位,在校正之后提升至14.8位。在无校正的情况下无杂散动态范围(SFDR)为81dB,在校正之后提升至100dB。
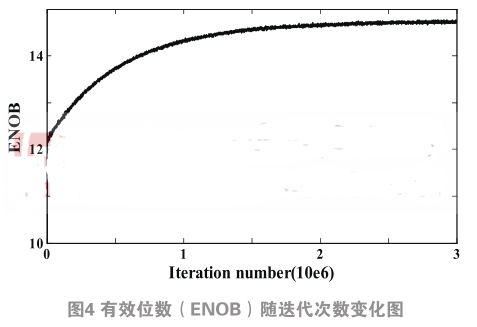
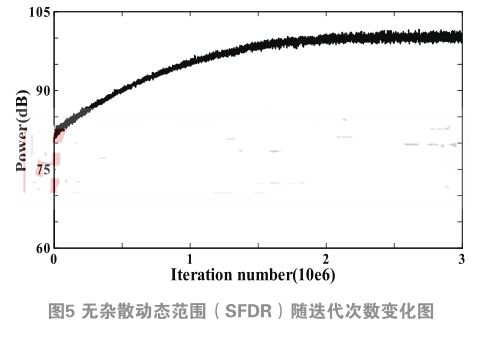
3、 结论
随着制造工艺的特征尺寸进入纳米量级,数字电路的集成度越来越高,同时电源电压也逐渐降低。但模拟电路并未像数字电路一样受益于工艺的进步,相反随着MOS管尺寸和电源电压减小,精确匹配、高增益和大摆幅等指标更难实现,因此,采用数字信号处理的方式来解决模拟电路中的非理想因素是一种趋势。本文提出了一种电容失配的数字后台校正方法,能实时跟随环境参数的变化,适用于SAR ADC,能有效消除电容之间的失配,明显地提高ADC性能。
责任编辑:gt
-
基于数字后处理算法的并行交替采样ADC系统2021-09-17 790
-
Matlab-LMS算法演示2021-08-17 1984
-
基于FPGA的自适应LMS算法的实现2021-05-28 1068
-
基于FPGA的定点LMS算法的实现讲解2021-04-28 997
-
什么是CORDIC算法?如何实现FPGA的数字频率校正?2019-09-19 2115
-
自适应LMS算法的C语言实时处理实现方法2019-05-21 2541
-
LMS自适应算法的FPGA设计与实现_陈亮2017-03-19 1080
-
时间交织ADC时间失配后台数字校准算法_邓红辉2017-01-08 814
-
浮点LMS算法的FPGA实现2011-09-19 1757
-
matlab实现LMS算法2011-08-31 1856
-
基于FPGA的横向LMS算法的实现2010-12-07 960
-
改进的LMS算法自适应滤波器的DSP实现2010-09-01 958
-
变步长LMS自适应滤波算法及其分析2010-04-26 3550
全部0条评论

快来发表一下你的评论吧 !

