基于DSP的MEMS陀螺误差建模与滤波方法分析

　　引言

　　随着微机电和惯性技术的发展，MEMS惯性器件技术越来越成熟，MEMS陀螺以其性能高、尺寸小、能耗低、可靠性高、重量轻、价格低等优点，在低成本姿态测量系统中的应用越来越广泛。但MEMS陀螺受制造工艺的限制，与传统工艺制造的惯性陀螺相比，在受到温度、外围电路的影响时，输出数据存在较大的随机噪声，影响其测量精度。为了降低随机噪声对系统测量精度的影响，必须根据大量的陀螺实际测量数据，建立准确的随机噪声模型，根据噪声模型选择合理有效的方法进行滤波补偿，提高系统的测量精度。在近几年MEMS陀螺的应用过程中，陀螺随机噪声模型建立的方法主要有小波分析、神经网络和时间序列分析法，滤波方法则是根据模型展开一定的数据处理，针对以上建模方法采用的主要滤波技术有质子滤波、鲁棒滤波、Kalman滤波以及改进滤波技术等［46］。

　　MEMS陀螺在姿态测量系统的实际应用中，为了实时采集系统的姿态信息，数据采集、处理、解算必须满足系统的实时性要求，小波分析、神经网络等方法建立的噪声模型通常具有较高的阶数，难以工程实现和满足系统的实时性要求。采用时间序列分析法，通过对陀螺随机噪声的AR建模，可以有效地建立常规陀螺的随机噪声模型。本文以小型无人机姿态测量系统应用为背景，根据系统设计中MEMS陀螺的实际测试数据，详细研究了针对其随机噪声数据的建模方法和Kalman滤波方法。

　　1陀螺误差建模

　　1.1原始数据采集

　　系统主控制器通过串行数据接口SPI与MEMS陀螺通信，陀螺角速率采样周期为20ms，在陀螺静止状态下进行20min的试验数据采集，图1为陀螺z轴在零点时的噪声原始数据，共10000组采样数据。

　　

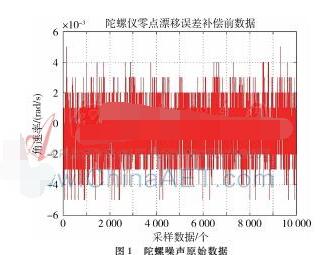
　　通过对MEMS陀螺噪声原始数据的分析可以得知，噪声包含随机漂移分量和常值项，去掉噪声中的常值项，所得的噪声样本序列是一个随机时间序列。根据时间序列分析方法对随机时间序列样本进行建模，该模型可以用来逼近真实的噪声数据，用时间序列模型对陀螺噪声进行预报，从而采用滤波技术去除噪声特性，提高系统测量精度［79］。

　　1.2数据预处理

　　MEMS陀螺噪声原始数据中包含常值分量和随机分量。常值分量可以通过均值方法提取，陀螺短时间工作时，可以通过这一方法进行补偿，长时间工作时，需要考虑自身的常值漂移量，简单地采用均值方法去除常值分量，无法得到有效的随机漂移序列。通过对陀螺测量数据进行分析，考虑陀螺原始数据采样周期和陀螺数据使用周期，本文采用实时移动平均算法对陀螺原始数据进行处理，以实时采集值和前面9个采样点的平均值作为当前时刻常值分量。采样点数的选择需要考虑实际应用的实时性和陀螺常值漂移特性，点数太少，则平均效果不好；点数太多，则直接影响陀螺测量的实时性，在无人机姿态控制中，直接影响系统的机动性和稳定性。

　　去除常值后的序列即为MEMS陀螺的随机噪声信号，是时间序列分析建模对象，在建模之初，对预处理后的MEMS陀螺仪随机噪声信号的平稳性、正态性进行判断，以确定预处理后的数据确实符合时间序列的建模要求。

　　1.3陀螺误差建模

　　经过数据预处理，对陀螺噪声数据进行时间序列建模，本文结合工程实际应用，考虑系统的实时性、适用性，结合考虑AIC准则，确定选用时间序列分析法的AR模型对陀螺随机噪声进行建模。

　　AR（p）模型一般格式为：

　　其中ap为模型回归系数，x（k）为模型输出，w（k）为模型噪声序列，p为模型阶数。

　　根据AIC最小标准确定陀螺漂移的数学模型，通过陀螺噪声特性的试验数据分析，选择AIC值最小的AR（1）作为陀螺漂移的模型。

　　陀螺AR（1）模型为：

　　x（k）=a1x（k－1）+w（k）（2）

　　其中a1为模型回归系数，x（k）为测量值，w（k）为噪声序列。

　　AR（1）模型回归系数a1可以通过陀螺在静止状态下测得的10000组噪声数据计算得到，通过MATLAB软件中Yule-Walker计算方法，得模型回归系数a1=0.77。

　　2卡尔曼滤波

　　2.1卡尔曼滤波方程的建立

　　Kalmann滤波在随机信号处理过程中根据系统噪声和观测噪声特性，以系统的观测量作为滤波器的输入，以所要估计值作为滤波器的输出，滤波器根据状态方程和观测方程估计出所需要的处理数据，在工程应用中简单且易于实现，是一种实时递推的最优估计方法。本文在建立陀螺噪声模型的基础上，以试验数据为系统观测量，采用Kalman滤波方法对陀螺噪声进行滤波。

　　根据建立的一阶AR（1）模型，通过离散Kalman滤波对陀螺采样数据进行最优估计，其状态方程为：

　　设Vk为测量噪声序列，则系统的观测方程为：

　　Zk=CXk+Vk（4）

　　式中C=［1，0］；Xk为根据陀螺采样数据获得的状态估计值，Wk为系统噪声，Zk为陀螺噪声测量值，Vk为观测噪声。根据陀螺静止状态的试验特性，可假设其系统噪声Wk和观测噪声Vk（k=0，1，2，3，…）的数学统计特性为E（Vk）=E（Wk）=0。

　　2.2滤波递推公式

　　根据状态方程、观测方程和Kalman滤波递推公式，可以得到整个系统的滤波算法。滤波器的输入Zk为零漂数据，设初始条件P0为二阶单位阵，0为［0，0］T。

　　实时状态预测阵：

　　k/k－1=Φk－1

　　协方差阵一步预测为：

　　Pk/k-1=ΦPk-1Φ+HQHT

　　滤波增益：

　　Kk=Pk/k-1CT（CPk/k-1CT+R）-1

　　状态估计：

　　k=k/k-1+Kk（ZK-Ck/k-1）

　　协方差阵估计更新：

　　Pk=（1-KkC）Pk/k-1

　　其中，各变量的意义如表1所示。

　　

　　3数据分析

　　

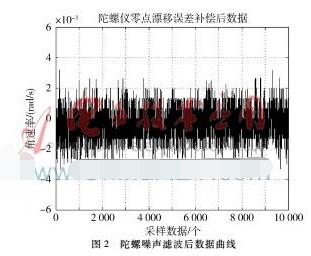
　　通过MATLAB对实测数据进行Kalman滤波分析，图2为Kalman滤波后陀螺仪零点数据输出曲线。陀螺噪声数据滤波前后的均值和方差见表2，滤波后噪声均值比滤波前减小30%，其方差与滤波前比较，小了1~2个数量级，通过均值和方差的分析比较可以看出，基于陀螺噪声AR（1）模型采取的Kalman滤波方法，可以有效降低陀螺噪声特性，其噪声分散程度也显著地减小了。陀螺噪声虑波后的数据曲线如图2所示。通过对比图1与图2的陀螺噪声曲线，可以直观地看到滤波前后数据变化。

　　4结论

　　本文通过试验仿真研究了MEMS陀螺的噪声特性，以真实的陀螺噪声数据为处理对象，设计实时性较好的数据预处理方法，对预处理后的数据采用时间序列分析法进行建模，通过Kalman滤波技术进行滤波处理。仿真试验表明，采用的噪声建模方法和滤波处理技术可以有效降低陀螺随机噪声特性，减小噪声随机分散程度，提高陀螺在姿态测量系统中的测量精度，提高MEMS陀螺的应用价值。