

基于FPGA器件实现乘法器因子求取模块的RS编码优化设计
可编程逻辑
描述
引言
里得-所罗门码(Reed-Solomon,RS)是由REED I S和SOLOMON G在1960年提出的一种特殊的非二进制BCH码,是所有(n,k)线性分组码中纠错能力最强的码型,可同时纠正随机错误和突发错误。随着大规模集成电路技术的发展,RS码凭借其优异的性能广泛应用于深空通信、移动通信、军用通信、光纤通信、磁盘阵列及光存储等领域,另外RS编码也可应用于保密通信中。
1、RS编码原理
对于码长为n=2m-1(n>2)的RS(n,k)码,其码元符号均取GF(2m),其信息段具有k个符号,监督段具有n-k个符号,可纠正t个突发错误,其生成多项式为:
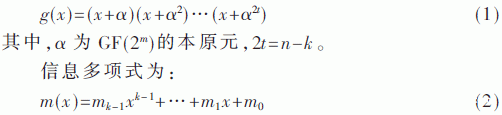
RS(n,k)编码的码多项式为:

其中,r(x)为RS(n,k)编码的校验多项式。
在实际应用中采用的RS码均为系统码,c(x)可被g(x)整除,mod为求余运算,则:

2、RS编码电路
根据RS编码原理可知,RS码的编码电路主要根据生成多项式g(x)进行设计,实际应用中的常用RS编码电路如图1所示。

图1中, g2t-1,g2t-2,…,g1,g0为生成多项式g(x)的系数:

电路工作前将所有寄存器清零,开关SW1接至mr处,开关SW2接至m处,信息码mk-1,…,m1,m0依次进入编码电路,并同时由输出端进行输出。当m(x)送入电路后,开关SW1接至0处,开关SW2接至r处,依次输出寄存器R2t-1,…,R1,R0的值,即校验子rn-k-1,…,r1,r0的值,从而完成RS(n,k)编码。
3、 基于FPGA的RS编码优化


其中,矩阵C为乘法器因子矩阵。观察RS编码电路可知,每个乘法器的系数gk为固定值,即RS编码电路每个乘法器的乘法器因子为固定值。因此,可以在编码前根据生成多项式g(x)的系数g2t-1,g2t-2,…,g1,g0的值生成乘法器因子矩阵C2t-1,C2t-2,…,C1,C0用于后续的RS编码。例如,RS(255,239)的生成多项式系数g15=118,对应的乘法器因子矩阵C15为:


由此证明通过乘法器因子矩阵可以把RS编码中信息码与生成多项式系数gk在伽罗华域上的乘法转换转为信息码数据位之间的加法运算。根据伽罗华域的加法运算法则,信息码数据位之间的伽罗华域加法运算在FPGA实现时可由异或操作(^)完成,从而使得FPGA实现伽罗华域的乘法运算简化,数据运算量减少。

4、RS编码优化后的FPGA实现
4.1 乘法器因子求取模块的FPGA实现

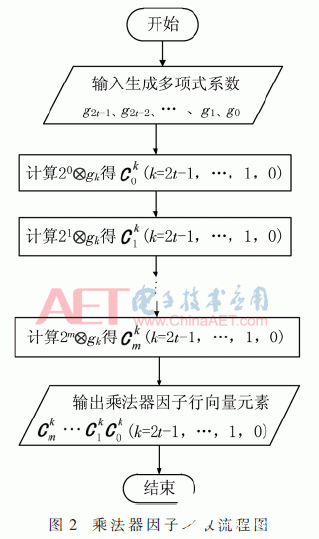
在FPGA中实现GF(28)域中RS(255,239)乘法器因子求取的结果如图3所示。

4.2 RS编码的FPGA实现
为了验证乘法器因子模块的有效性,采用所得的乘法器因子进行RS编码,将编码结果与MATLAB计算的理论结果进行对比验证[15]。
RS编码的RTL原理图如图4所示,包括信息码数据缓存模块m_fifo、控制模块control、校验码生成模块R_top、编码数据输出模块c_fifo。其中,校验码生成模块R_top中包含乘法器因子求取模块,由其完成乘法器因子的求取。
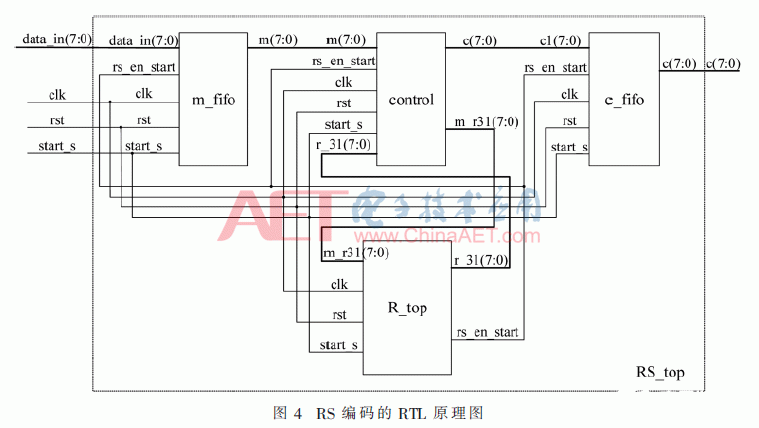
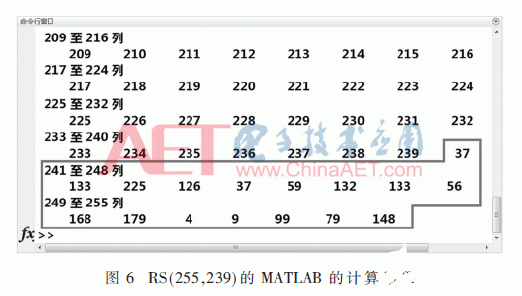
采用乘法器因子模块所得的乘法器因子实现的RS(255,239)编码的测试结果如图5所示。当输入信息码data_in为(1,2,3,…,238,239)时,校验码生成模块R_top生成的16个校验子为(37,133,225,126,37,59,132,133,56,168,179,4,9,99,79,148)。图6为MATLAB对(1,2,…,239)进行RS(255,239)编码输出的计算结果,将图6的输出结果与图5的输出码字c进行对比,可以验证采用乘法器因子求取模块实现的RS编码无误。

4.3 乘法器因子求取模块的适应性验证
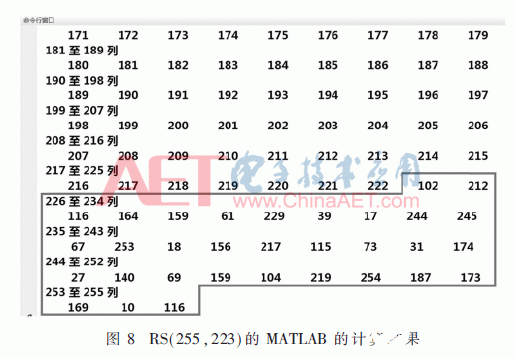
为了验证乘法器因子求取模块的适应性,采用乘法器因子求取模块完成RS(255,223)的乘法器因子求取,输入data_in为(0,1,2,…,222),RS(255,223)编码测试结果如图7所示,编码输出的32个校验子为(102,212,116,164,159,61,229,39,17,244,245,67,253,18,156,217,115,73,31,174,27,140,69,159,104,219,254,187,173,169,10,116)。将编码输出与图8所示RS(255,223)编码计算结果进行比对,可验证编码无误,证明采用乘法器因子求取模块优化的基于FPGA的RS编码可适应不同的生成多项式,完成有效RS编码。

5、 结论
RS编码是一类很好线性纠错码,在工程实践中有着广泛应用。本文通过设计乘法器因子求取模块,将RS编码中信息码与乘法器系数在伽罗华域上乘法转换转为信息码数据位之间的加法运算,降低FPGA实现时的运算复杂度、减少运算量,且可根据不同的乘法器系数生成相应的乘法器因子,完成不同码长和校验子的RS编码,可广泛应用于短码及中长码通信领域,具有很好的实际应用价值。
责任编辑:gt
-
E203在基于wallace树+booth编码的乘法器优化后的跑分结果2025-10-27 112
-
关于E203内核高性能乘法器优化(一)2025-10-23 124
-
蜂鸟E203内核乘法器的优化2025-10-22 103
-
优化boot4乘法器方法2025-10-21 147
-
FPGA常用运算模块-加减法器和乘法器2023-05-22 7162
-
基于FPGA的16位乘法器的实现2021-06-01 1737
-
乘法器原理_乘法器的作用2021-02-18 28081
-
怎么设计基于FPGA的WALLACETREE乘法器?2019-09-03 2010
-
使用verilogHDL实现乘法器2018-12-19 11507
-
FPGA乘法器设计2018-02-25 4915
-
基于FPGA的WALLACE TREE乘法器设计2011-11-17 5837
-
基于IP核的乘法器设计2011-05-20 1027
-
乘法器的基本概念2010-05-18 15368
全部0条评论

快来发表一下你的评论吧 !

