

人脸识别的过程_人脸识别方法
触控感测
描述
人脸识别的过程
人脸识别是现下非常火热的话题,市场前景被看好,随着生物识别技术的普及以及运用,人脸识别也揭开了其神秘的面纱,今天就带大家了解一下人脸识别技术的流程。
说起人脸识别流程,其实概况来说主要是人脸图像采集及检测、人脸图像预处理、人脸图像特征提取以及匹配与识别。一起来简单了解每一个部分。
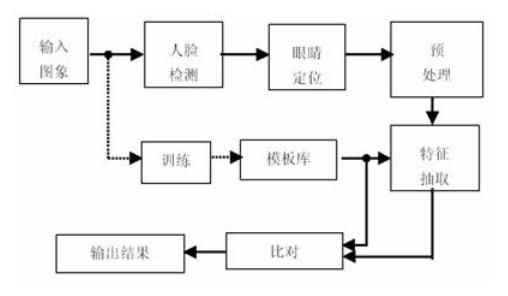
人脸图像采集及检测
顾名思义就是人脸录入系统,一般是批量录入,用户主动通过录入端口上传导入自己的人脸。另外一种就是现场视频人脸图像采集,类似于办身份证,当场摄像头采集面部,当人人脸识别的采集需要在指定摄像范围内,采集设备自动搜索客户的人脸图像。
支付宝的人脸识别支付加入了活体检测,需要让客户做一系列动作,比如说张嘴, 抬头、低头,左转头、右转头,眨眼睛等,人脸识别技术也是在不断的进步,活动检测可有效抵御照片、换脸、面具、遮挡以及屏幕翻拍等常见的攻击手段。
人脸图像预处理
人脸图像预处理是对系统所采集到的人脸图像进行光线处理、切割、旋转、降噪、过滤、放大或缩小等一系列的复杂处理,通过这些处理使人脸图像无论是光线还是角度、距离、大小等达到人脸图像特征提取的标准要求,尽可能消除因光照和角度等因素造成的影响,为进行人脸图像特征提取做好准备。
匹配与识别
● 人脸识别1:1比对
宇松科技人脸识别系统通过人脸识别算法实现上两张图像进行比对,根据不同渠道的识别率返回比对结果,并将比对通过的图像按照设定规则入库保存。能够最大限度的提高识别率,智能的解决像素较低(如芯片图)、逆光、侧光、昏暗、带眼镜、一定角度侧脸等不利条件。
● 人脸识别1:N比对
宇松科技人脸识别系统通过客户图像,在客户特征库中识别出该将客户身份,并返回该客户的相关信息,如客户信息号、姓名等。系统具有人脸识别 1:N功能,对外提供 1:N比对接口,可根据各系统传送的照片提取特征值,并跟库中模板比对,返回相似度最高的N个人(返回人数可自定义)。
人脸识别目前主要运用在银行VIP客户身份识别、教育领域的考生身份识别、通关口岸、门禁考勤、智能视频监控等。
人脸识别分析算法
人脸识别技术中被广泛采用的区域特征分析算法,它融合了计算机图像处理技术与生物统计学原理于一体,利用计算机图像处理技术从视频中提取人像特征点,利用生物统计学的原理进行分析建立数学模型,即人脸特征模板。利用已建成的人脸特征模板与被测者的人的面像进行特征分析,根据分析的结果来给出一个相似值。通过这个值即可确定是否为同一人。
人脸识别的方法很多,主要的人脸识别方法有:
(1)几何特征的人脸识别方法:几何特征可以是眼、鼻、嘴等的形状和它们之间的几何关系(如相互之间的距离)。这些算法识别速度快,需要的内存小,但识别率较低。
(2)基于特征脸(PCA)的人脸识别方法:特征脸方法是基于KL变换的人脸识别方法,KL变换是图像压缩的一种最优正交变换。高维的图像空间经过KL变换后得到一组新的正交基,保留其中重要的正交基,由这些基可以张成低维线性空间。如果假设人脸在这些低维线性空间的投影具有可分性,就可以将这些投影用作识别的特征矢量,这就是特征脸方法的基本思想。这些方法需要较多的训练样本,而且完全是基于图像灰度的统计特性的。目前有一些改进型的特征脸方法。
(3)神经网络的人脸识别方法:神经网络的输入可以是降低分辨率的人脸图像、局部区域的自相关函数、局部纹理的二阶矩等。这类方法同样需要较多的样本进行训练,而在许多应用中,样本数量是很有限的。
(4)弹性图匹配的人脸识别方法:弹性图匹配法在二维的空间中定义了一种对于通常的人脸变形具有一定的不变性的距离,并采用属性拓扑图来代表人脸,拓扑图的任一顶点均包含一特征向量,用来记录人脸在该顶点位置附近的信息。该方法结合了灰度特性和几何因素,在比对时可以允许图像存在弹性形变,在克服表情变化对识别的影响方面收到了较好的效果,同时对于单个人也不再需要多个样本进行训练。
(5)线段Hausdorff 距离(LHD) 的人脸识别方法:心理学的研究表明,人类在识别轮廓图(比如漫画)的速度和准确度上丝毫不比识别灰度图差。LHD是基于从人脸灰度图像中提取出来的线段图的,它定义的是两个线段集之间的距离,与众不同的是,LHD并不建立不同线段集之间线段的一一对应关系,因此它更能适应线段图之间的微小变化。实验结果表明,LHD在不同光照条件下和不同姿态情况下都有非常出色的表现,但是它在大表情的情况下识别效果不好。
(6)支持向量机(SVM) 的人脸识别方法:支持向量机是统计模式识别领域的一个新的热点,它试图使得学习机在经验风险和泛化能力上达到一种妥协,从而提高学习机的性能。支持向量机主要解决的是一个2分类问题,它的基本思想是试图把一个低维的线性不可分的问题转化成一个高维的线性可分的问题。通常的实验结果表明SVM有较好的识别率,但是它需要大量的训练样本(每类300个),这在实际应用中往往是不现实的。而且支持向量机训练时间长,方法实现复杂,该函数的取法没有统一的理论。
- 相关推荐
- 热点推荐
- 人脸识别
-
【TL6748 DSP申请】基于DSP的人脸识别技术2015-09-10 2804
-
人脸识别的研究范围和优势2017-06-29 4158
-
LabVIEW人脸识别设计2019-04-28 6259
-
人脸识别的三大模式2019-08-06 4880
-
什么是人脸识别技术2021-03-03 3881
-
人脸识别常用方法研究2009-09-14 472
-
基于GLCM和CGA的人脸表情识别方法2015-11-18 911
-
基于EHMM-SVM的人脸识别方法2017-11-21 885
-
人脸识别的原理2019-03-04 13231
-
人脸识别的原理说明2020-06-17 4148
-
何为人脸识别_人脸识别的应用场景2020-10-30 3670
-
人脸识别的优点和识别方法2023-02-06 1140
-
生物识别和人脸识别的区别2023-08-28 2848
-
人脸检测与识别的方法有哪些2024-07-03 2092
-
如何设计人脸识别的神经网络2024-07-04 1519
全部0条评论

快来发表一下你的评论吧 !

