

基于通用阻抗变换器的S变换实现高通滤波器的设计
模拟技术
描述
引言
在音频系统中,为了避免因采用半导体或其它有源器件带来的非线性和频率特性畸变,保证实现平坦而宽阔的高频响应,通常选用分立元件构成的滤波器来满足DSD(直接数据流)对频率带宽的苛刻要求。而在分立元件有源滤波器的设计与实现过程中,通常要寻找大量数值不同、但精度要求十分严格的元件又非常困难。而采用通用阻抗变换器(GIC)由于电路中只有固定电阻和电容,利用若干个可变数值电阻即可完成电路设计,所以实现起来异常方便。下面就将其具体设计及应用方法加以详细分析。该方法中的l/S变换实现法可用于设计低通滤波器,而S变换实现法则可用于设计高通滤波器。
1、 通用阻抗变换器
通用阻抗变换器(GIC)的典型电路如图1所示,其驱动点阻抗ZIN可以表示为:

如果把Z4变换为阻抗为1/SC(其中S=jω)的虚拟元件,其它元件为电阻,则驱动点的阻抗为:

这样,该阻抗即与频率成正比,它相当于一个电感,可计算其电感值为:
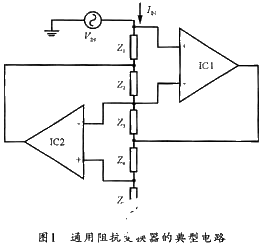

如果引入两个电容取代Z1和Z3,而Z2、Z4、Z5仍为电阻,则驱动点的阻抗表达式可变为:

可见,该阻抗正比于1/S2,可称为D元件。它的驱动点阻抗为:

如果令C=1F、R2=R5=1 Ω、R4=R,则D可化简为:D=R。为了更好地说明D元件的特性,如将S=jω带入式(5),则有:

2、 高通变换的实现
事实上,通用阻抗变换器(GIC)也可作为模拟电感使用,其电感值为L=CR1R3R5/R2。若取R1=R2=R3=1 Ω,C=1F,则可得到归一化电感L=R5。这种模拟电感特别适合作为高通臂接地电感。
下面给出通用阻抗变换器(GIC)的另一种应用,即S变换实现法。
所谓S变换,就是用S乘以R、C、L。其结果就是把电阻变换为电感,电容变换为电阻,并将电感变换为频变电阻。但这里的频变电阻是与S2成正比的。图2给出了S变换的元件变换关系图。
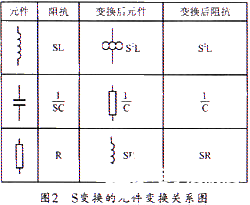
下面给出用GIC实现S2L变换具体应用方法。本设计要求在高通1590 Hz处的最大衰减为0.1773dB,而在465 Hz处的最小衰减为40 dB。其具体的实现方法如下:
(1) 计算陡度系数:ΩS=fC/fS=1590/465=3.4194;
(2) 因滤波特性非常陡峭,所以选择椭圆函数型,参数如下:
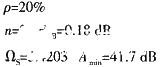
此时对应的归一化低通电路如图3所示,它表明的是低通原型;
(3) 为了将网络转换为归一化高通模式,可用电容代替电感,其元件值为其倒数。归一化高通模式的电感也取电容值的倒数,其电路如图4所示。
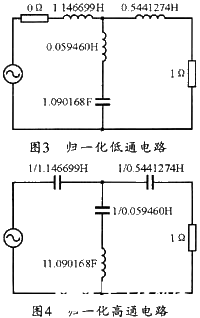
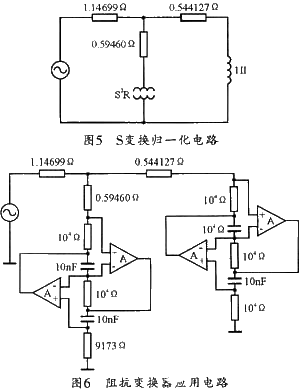
(4) 对图4取S变换,将电容取倒数变为电阻,将电阻代替为电感,并将电感用频变负阻代替,即可获得如图5所示的S变换归一化电路;
(5) 继续反归一化即可得到实际元件值,并最终得到如图6所示的实际电路。
3 、结束语
一般情况下,1/S变换实现法可用于低通滤波器的设计。S变换实现法可用于高通滤波器的设计。目前,通用阻抗变换器GIC(generalimpedance converter)的S变换实现法已可广泛应用于音频系统和超音频系统的滤波器。事实上,本设计方法已经多次在设计中使用,效果良好。
责任编辑:gt
-
阻抗变换器的形式有哪些2024-08-28 1891
-
高频共模电流、电压和阻抗的测量 —— 以反激变换器为例2021-12-21 9091
-
通用阻抗变换器在有源滤波器中有什么用?2021-04-14 1816
-
阻抗变换器是什么2019-04-15 10021
-
双波段阻抗变换器2011-02-25 660
-
矩阵变换器的阻尼输入滤波器设计2010-02-19 576
-
阻抗变换器电路2010-01-11 6282
-
DC/DC变换器中输出滤波器的比较2009-07-09 2101
-
高通滤波器设计2008-12-01 3880
-
负阻抗变换器2008-09-24 13331
全部0条评论

快来发表一下你的评论吧 !

