

指定石英晶体-Specifying Quartz Cryst
通信设计应用
63人已加入
描述
Abstract: This article explains the specifications and characteristics of crystals and crystal oscillators, and aids in specifying crystals and working with crystal vendors. The article covers the significant performance characteristics of crystals, which include resonance frequency, resonance mode, load capacitance, series resistance, holder capacitance, motional inductance and capacitance, temperature calibration, and drive level.
A quartz crystal can be modeled as a series LRC circuit in parallel with a shunt capacitor. Figure 1 shows this generic circuit model.
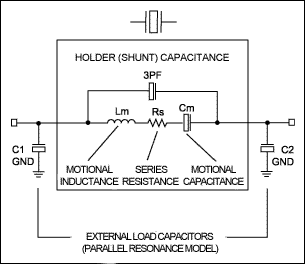
Figure 1. Generic crystal model (fundamental mode).
We will now look at each key performance specification in detail.
An overtone is similar in concept to a harmonic, except that crystal oscillation overtones are not exact integer multiples of the fundamental. Overtone selection is based on using the lowest possible overtone that will result in a crystal's fundamental frequency below 30MHz. The vendor calibrates a 3rd overtone crystal at the 3rd overtone, not the fundamental. Most crystal vendors, for example, will automatically give you a 3rd overtone 50MHz crystal if you do not specify fundamental mode or an overtone mode. If you plug a 50MHz, 3rd overtone crystal into an oscillator circuit designed for a fundamental-mode crystal, you are likely to have an oscillator running at 50/3 or 16.666MHz! If you do not know the frequency mode of your crystal, contact the designer or the manufacturer of the oscillator circuit.
Crystal vendors provide overtone crystals because quartz material becomes thinner and thinner as frequency increases. Crystals between 15MHz to 30MHz are specified in either a fundamental or 3rd overtone. Starting at about 30MHz, the quartz becomes so thin that it is hard to handle during the manufacturing process, and crystal vendors do not like handling thin quartz. Given the extra manufacturing effort involved with thin quartz, choosing a crystal specified at an overtone mode instead of the fundamental mode can be significantly less expensive.
A recent invention in quartz crystal processing is inverted mesa crystals, which can be manufactured with a thinner structure at higher fundamental-mode frequencies. Inverted mesa crystals provide two significant advantages: they enable less complex high-frequency oscillator designs; they reduce component count by avoiding the need for external inductors/capacitors to induce the proper overtone oscillation mode from the crystal. . The manufacturers of inverted mesa crystals can specify fundamental-mode crystals considerably higher than 30MHz. Note, however, that not all crystal vendors can provide inverted mesa technology. Remember, that an overtone-mode crystal cannot be used in a fundamental-mode oscillator, and vice versa. In that situation the overtone-mode crystal may oscillate, but not at the correct frequency.
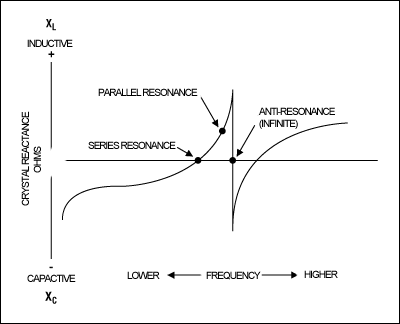
Figure 2. Crystal impedance versus frequency.
With a series-resonant crystal, you can ignore the load capacitance specification. This is true because the crystal's motional inductance and motional capacitance are the only LC components that determine oscillation frequency.
In Figure 2, the anti-resonance occurs when the net inductive component of the crystal model resonates with the crystal's internal holder capacitance. Anti-resonance is not used for oscillator designs.
An exception to the above guideline is 32.768kHz wristwatch crystals, where series resistance can be in the tens of kilohms. Consequently, for this application the oscillator circuit must accommodate this high series resistance. Failure to address this will result in a 32.768kHz oscillator that does not oscillate. You should not expect to use an oscillator designed for a 10MHz crystal with a 32.768kHz crystal. It will not work.
At first glance, crystals can seem simple elements that one merely plugs into the circuit. An analysis of the actual circuit model and an understanding of key parameters, however, reveals their complexity and also simplifies the process of designing them into your next application. The following handy Crystal Specification Worksheet will help you specify and order quartz crystals.
Table 1. Crystal Specification Worksheet
Table 2. Partial List of Crystal Vendors
打开APP阅读更多精彩内容
Introduction
Quartz is a piezoelectric material that moves when placed in an electric field. A quartz crystal is a vibrating piece of quartz. Quartz crystals are available in a myriad of shapes and sizes, and can range widely in performance specifications. These specifications include resonance frequency, resonance mode, load capacitance, series resistance, holder capacitance, motional inductance and capacitance, temperature calibration, and drive level. If you understand these parameters and how they relate to the crystal's performance, you will successfully specify crystals for your application.A quartz crystal can be modeled as a series LRC circuit in parallel with a shunt capacitor. Figure 1 shows this generic circuit model.

Figure 1. Generic crystal model (fundamental mode).
We will now look at each key performance specification in detail.
Resonance Frequency
Crystals below 30MHz are often specified at the fundamental frequency; above 30MHz they are typically specified as 3rd, 5th, or even 7th overtone. (Overtones occur only at odd multiples.) Consequently, it is important to know whether the oscillator is operating in fundamental or overtone mode.An overtone is similar in concept to a harmonic, except that crystal oscillation overtones are not exact integer multiples of the fundamental. Overtone selection is based on using the lowest possible overtone that will result in a crystal's fundamental frequency below 30MHz. The vendor calibrates a 3rd overtone crystal at the 3rd overtone, not the fundamental. Most crystal vendors, for example, will automatically give you a 3rd overtone 50MHz crystal if you do not specify fundamental mode or an overtone mode. If you plug a 50MHz, 3rd overtone crystal into an oscillator circuit designed for a fundamental-mode crystal, you are likely to have an oscillator running at 50/3 or 16.666MHz! If you do not know the frequency mode of your crystal, contact the designer or the manufacturer of the oscillator circuit.
Crystal vendors provide overtone crystals because quartz material becomes thinner and thinner as frequency increases. Crystals between 15MHz to 30MHz are specified in either a fundamental or 3rd overtone. Starting at about 30MHz, the quartz becomes so thin that it is hard to handle during the manufacturing process, and crystal vendors do not like handling thin quartz. Given the extra manufacturing effort involved with thin quartz, choosing a crystal specified at an overtone mode instead of the fundamental mode can be significantly less expensive.
A recent invention in quartz crystal processing is inverted mesa crystals, which can be manufactured with a thinner structure at higher fundamental-mode frequencies. Inverted mesa crystals provide two significant advantages: they enable less complex high-frequency oscillator designs; they reduce component count by avoiding the need for external inductors/capacitors to induce the proper overtone oscillation mode from the crystal. . The manufacturers of inverted mesa crystals can specify fundamental-mode crystals considerably higher than 30MHz. Note, however, that not all crystal vendors can provide inverted mesa technology. Remember, that an overtone-mode crystal cannot be used in a fundamental-mode oscillator, and vice versa. In that situation the overtone-mode crystal may oscillate, but not at the correct frequency.
Resonance Mode
Crystals have two modes of resonance, parallel and series, and all crystals exhibit both resonance modes. The oscillator circuit is calibrated for one mode or the other, but not both. For applications requiring no tighter than 100ppm frequency accuracy, resonance mode is usually not an issue. If you are attempting to control frequency (or time) to within 100ppm, however, the resonance-mode specification becomes important. The crystal vendor's principal concern is in which mode the crystal is calibrated during manufacturing. Knowing that information, the crystal vendor then sets up an oscillator circuit with the crystal in a customer-specified series resonance or parallel resonance, and calibrates the crystal. Figure 2 shows crystal impedance behavior versus frequency, and the relative location of each resonance mode.
Figure 2. Crystal impedance versus frequency.
Load Capacitance
Load capacitance is an important specification when using parallel-resonant oscillation mode. Figure 2 shows that crystal parallel-resonance mode is always above the series resonance frequency and is characterized by inductive reactance. In parallel-resonance oscillation mode, the crystal's inductance (motional inductance) is in parallel with the oscillator's load capacitance, thereby forming an LC tank circuit. This LC determines the oscillator frequency. If your oscillator uses parallel resonance, the crystal vendor must know the load capacitance employed by the oscillator circuit. The load capacitance is simply the amount of external circuit capacitance in parallel with the crystal itself when it is placed in the oscillator circuit. The crystal vendor will then ensure that your crystal is calibrated at the factory using this same load capacitance. Vendors are flexible regarding load capacitance. Ask them what range of load capacitance can you specify. Your oscillator should fall within the crystal vendor's acceptable range of load capacitance.With a series-resonant crystal, you can ignore the load capacitance specification. This is true because the crystal's motional inductance and motional capacitance are the only LC components that determine oscillation frequency.
In Figure 2, the anti-resonance occurs when the net inductive component of the crystal model resonates with the crystal's internal holder capacitance. Anti-resonance is not used for oscillator designs.
Series Resistance
Series resistance is the effective resistive component in series with the LC model of the crystal itself (see Figure 1). Oscillator circuits can tolerate some degree of series resistance, but not too much. A typical range is 25Ω to 100Ω for most crystals. The crystal vendor usually characterizes this resistance and specifies typical or maximum values for series resistance. Excessive crystal series resistance can lead to oscillator startup failure, so sufficient margin must be built into the oscillator design.An exception to the above guideline is 32.768kHz wristwatch crystals, where series resistance can be in the tens of kilohms. Consequently, for this application the oscillator circuit must accommodate this high series resistance. Failure to address this will result in a 32.768kHz oscillator that does not oscillate. You should not expect to use an oscillator designed for a 10MHz crystal with a 32.768kHz crystal. It will not work.
Holder Capacitance
All crystals have small electrodes that connect the crystal to the package pins. The electrodes form a shunt capacitance in parallel with the crystal's LC model, as shown in Figure 1. Depending on the crystal's size and package, the holder capacitance can vary. Typical values range from 2pF to 6pF. Some oscillators will not tolerate excessive holder capacitance. This is particularly true at higher frequencies as the reactance of the holder capacitance decreases. Make sure the crystal vendor's holder capacitance is within the allowable range for your oscillator. As a general rule, minimize the holder capacitance (the smaller, the better).Motional Inductance and Capacitance
Motional inductance and capacitance are specifications provided by the crystal vendor. They describe the L and C values that comprise the crystal's electrical LC model. The extreme ratio of L to C is noteworthy, as it results in very large inductive and capacitive reactance values at the operating frequency. These large values are what give a crystal its extraordinarily high 'quality factor', also referred to as 'Q'. (Q is the ratio of energy stored to energy dissipated, also defined as the ratio of reactance to series resistance at the resonant frequency.) For an LRC circuit, Q = 1/R * sq. rt. (L/C). (The derivation of this is beyond the scope of this article.) A high Q is desirable, because higher Q values mean less frequency shift for a change in oscillator load capacitance and less shift due to other external factors such as oscillator supply voltage. Depending on your application, your oscillator circuit may or may not require specification of motional inductance and capacitance.Temperature Calibration
The frequency of the quartz crystal varies with temperature. The amount of frequency variation depends on the angle at which the quartz is cut from the original crystal. As the tolerance of the frequency becomes tighter, the temperature range reduces. An AT cut crystal is most commonly used for its highest stability over a wide temperature range.Drive Level
The power dissipated in the crystal must be limited or the quartz crystal can actually fail due to excessive mechanical vibration. Crystal characteristics also change with drive level due to nonlinear behavior. Analyze the oscillator design to determine the power dissipated in the crystal. Power dissipated is the product of crystal current squared times crystal series resistance. For a parallel-resonant oscillator, the crystal current equals the RMS voltage across the load capacitor divided by the load capacitor's reactance at the oscillator frequency. For a series-resonant crystal, the crystal current is the RMS voltage across the crystal divided by the crystal internal series resistance. The crystal manufacturer will specify maximum drive levels for a particular product line.Summary Observations
Expect crystal usage to increase as crystals appear in more products that use microcontrollers, digital signal processors, and data converters. Crystal technology is also moving forward, resulting in better performance and lower costs. At present, a higher frequency can be inexpensively obtained by devices that employ phase locked loops (PLLs) such as the MAX9471/MAX9472 that output a signal up to 200MHz from a minimum 5MHz quartz crystal input. By using fiber technology in conjunction with PLLs such as the MAX3610, a higher performance output signal of 212.5MHz is obtained with jitter as low as 0.7psRMS from a 26.56MHz crystal input.At first glance, crystals can seem simple elements that one merely plugs into the circuit. An analysis of the actual circuit model and an understanding of key parameters, however, reveals their complexity and also simplifies the process of designing them into your next application. The following handy Crystal Specification Worksheet will help you specify and order quartz crystals.
Table 1. Crystal Specification Worksheet
| Parameter | Comments |
| Frequency | Above 30MHz, specify overtone number. |
| Resonance mode | Specify parallel or series. |
| Load capacitance | Check with oscillator designer/vendor. |
| Series resistance | Specify maximum value, obtained from oscillator Designer. |
| Holder capacitance | Crystal manufacturer will provide. |
| Motional inductance and capacitance | Varies with manufacturer. |
| Drive level | Typically a maximum number obtained from the crystal vendor. |
Table 2. Partial List of Crystal Vendors
| Company | Toll-Free Number | Contact Number | Website Address | City, State (USA) |
| International Crystal Manufacturing (ICM) | (800) 725-1426 | (405) 236-3741 | www.icmfg.com/ | Oklahoma City, OK |
| Jan Crystals | (800) 526-9825 | (239) 936-2397 | www.jancrystals.com | Ft. Meyers, FL |
| ECS International | (800) 237-1041 | (913) 782-7787 | www.ecsxtal.com | Olathe, KS |
| CTS Reeves Frequency Products | (815) 786-8411 | www.ctscorp.com | Sandwich, IL | |
| CTS Reeves Frequency Products | (717) 243-5929 | www.ctscorp.com | Carlisle, PA | |
| Crystal Works, a Division of Connor Winfield | (405) 273-1262 | www.conwin.com | Shawnee, OK |
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
- 相关推荐
- 石英晶体
-
石英晶体器件基础2008-11-24 0
-
石英晶体的工作原理2013-12-20 0
-
石英晶体2014-01-15 0
-
透过石英晶体来看石英晶振的不可替代性2016-04-15 0
-
石英晶体的结构,有哪些基本特性?2021-03-15 0
-
石英晶体好坏怎么判断2021-05-10 0
-
石英晶体的等效模型是什么?石英晶体阻抗与频率之间有什么关系?2023-02-20 0
-
金属电极对高阶泛音石英晶体谐振器振动频率的影响2008-11-24 492
-
石英晶体谐振器2010-04-16 2051
-
陶瓷谐振器与石英晶体谐振器的区别2022-04-06 3238
-
石英晶体谐振器——国产替代需求强劲2023-02-17 1502
-
指定石英晶体2023-03-01 620
-
石英晶体谐振器的组成和参数2024-07-16 927
-
压控晶体振荡器和石英晶体振荡器的区别2024-09-25 440
全部0条评论

快来发表一下你的评论吧 !

